基数排序就这么简单-原创手记-慕课网

tags: 算法

一、基数排序(桶排序)介绍

来源360百科：

基数排序(radix sort)属于"分配式排序"(distribution sort)，又称"桶子法"(bucket sort)或bin sort，顾名思义，它是透过键值的部份资讯，将要排序的元素分配至某些"桶"中，藉以达到排序的作用，基数排序法是属于稳定性的排序，其时间复杂度为O (nlog(r)m)，其中r为所采取的基数，而m为堆数，在某些时候，基数排序法的效率高于其它的稳定性排序法。

从上面的简单介绍，是并不了解基数排序是怎么弄的～基数排序不同与其他的7种排序，其他7种排序本质上都是按照交换或者比较来进行排序，但是基数排序并不是，它是按照分配，回收(分配到不同的位置上，然后回收)..不断分配..回收来进行排序，直到有序..

听上去好像很高大上，很难的样子，其实不然。基数排序挺简单的，下面我就来看一下基数排序的流程....

我们有9个桶，将数组的数字按照数值分配桶中：

ps:图片来源于网络，侵删

上面我们发现：如果将桶按顺序进行回收，那么我们的排序就完成了～

可是，一般我们的数组元素都不仅仅是个位数的数字的呀，那么高位数的数字又怎么弄呢？？比如：23,44,511,6234这些高位数..

其实也是一样的：

第一趟桶排序将数字的个位数分配到桶子里面去，然后回收起来，此时数组元素的所有个位数都已经排好顺序了
第二趟桶排序将数字的十位数分别分配到桶子里面去，然后回收起来，此时数组元素的所有个位数和十位数都已经排好顺序了(如果没有十位数、则补0)
第三趟桶排序将数字的百位数分别分配到桶子里面去，然后回收起来，此时数组元素的所有个位数和十位数和百位数都已经排好顺序了(如果没有百位数、则补0)
..................................
直至全部数(个、十、百、千位...)排好顺序，那么这个数组就是有序的了。

ps:图片来源于网络，侵删

机智的同学可能就会发现了，关于这个桶我们可以用二维数组来进行存放。

10个桶子就是10列，如果分配时有的数字相同的话，那么就弄成多行~

二、基数排序体验

首先我们有以下这个数组：


   int[] arrays = {6,  4322, 432, 344, 55 };

现在我们有10个桶子，每个桶子下能装载arrays.length个数字..


int[][] buckets = new int[arrays.length][10];

效果如下：

2.1第一趟分配与回收

将数组的每个个位数进行分配到不同的桶子上：

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{4322,432,344,55,6}

2.2第二趟分配与回收

将数组的每个十位数进行分配到不同的桶子上(像6这样的数，往前边补0)：

于是我们可以得到这样的排序：

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,4322,432,344,55}

2.3第三趟分配与回收

将数组的每个百位数进行分配到不同的桶子上(像6、55这样的数，往前边补0)：

于是我们可以得到这样的排序：

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,55,4322,344,432}

2.3第四趟分配与回收

将数组的每个百位数进行分配到不同的桶子上(像6、55，344，432这样的数，往前边补0)：

于是我们可以得到这样的排序：

分配完之后，我们按照顺序来进行回收：得到的结果应该是这样子的：{6,55,344,432,4322}

此时我们的数组就已经可以排好序了~~~过程就是这样子，其实不难就只有两个步骤：

将数组的每一位放进桶子里
回收
循环......

三、基数排序代码编写

我们的基数排序是按照个、十、百、千位...来进行存放的。前面的演示是已经知道数组元素的数据的情况下来进行存放，但是一般我们是不去理会数组内元素的值的。那如果位数很多(万位)或者都是个位数，这个条件我们怎么去处理呢？

我们可以这样做：先求出数组最大的值，然后不断/10，只要它能大于0，那么它的位数还有~：

3.1求出数组最大的值

这个我在前面写递归的时候就有这个代码了，我就直接搬去递归的代码过来了，顺便复习一哈吧：

当然了，更好的是直接用for循环来找出来就行了(易读性好一些)


    /**
     * 递归，找出数组最大的值
     * @param arrays 数组
     * @param L      左边界，第一个数
     * @param R      右边界，数组的长度
     * @return
     */

    public static int findMax(int[] arrays, int L, int R) {

        //如果该数组只有一个数，那么最大的就是该数组第一个值了
        if (L == R) {
            return arrays[L];
        } else {

            int a = arrays[L];
            int b = findMax(arrays, L + 1, R);//找出整体的最大值

            if (a > b) {
                return a;
            } else {
                return b;
            }
        }

3.2代码实现


    public static void radixSort(int[] arrays) {

        int max = findMax(arrays, 0, arrays.length - 1);

        //需要遍历的次数由数组最大值的位数来决定
        for (int i = 1; max / i > 0; i = i * 10) {

            int[][] buckets = new int[arrays.length][10];

            //获取每一位数字(个、十、百、千位...分配到桶子里)
            for (int j = 0; j < arrays.length; j++) {

                int num = (arrays[j] / i) % 10;

                //将其放入桶子里
                buckets[j][num] = arrays[j];
            }

            //回收桶子里的元素
            int k = 0;

            //有10个桶子
            for (int j = 0; j < 10; j++) {
                //对每个桶子里的元素进行回收
                for (int l = 0; l < arrays.length ; l++) {

                    //如果桶子里面有元素就回收(数据初始化会为0)
                    if (buckets[l][j] != 0) {
                        arrays[k++] = buckets[l][j];

                    }

                }

            }

        }
    }

搞了一堆数测试了一哈：

四、总结

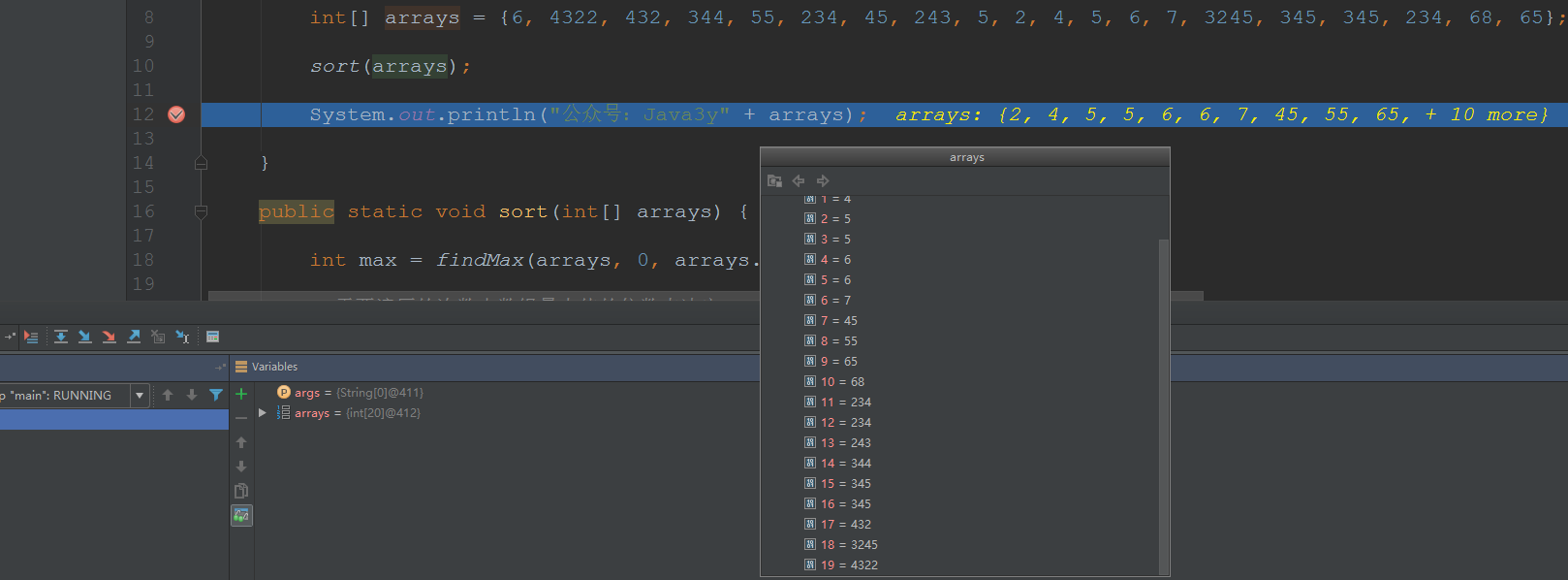
基数排序(桶排序)要理解起来并不困难，不过值得注意的是：基数排序对有负数和0的数列难以进行排序

因此，往往有0和负数的数组一般我们都不用基数来进行排序

基数排序的要点就两个：

分配：按照元素的大小来放入不同的桶子里
回收：将桶子里的元素按桶子顺序重新放到数组中
重复.....两个步骤

参考资料：