Ⅰ、三角数字
首先我们来看一组数字:1,3,6,10,15,21.....,在这个数列中第n项是由n-1项加n得到的,这个序列中的数字称为三角数字因为他们可以形象化地表示成一个三角形排列。如下图
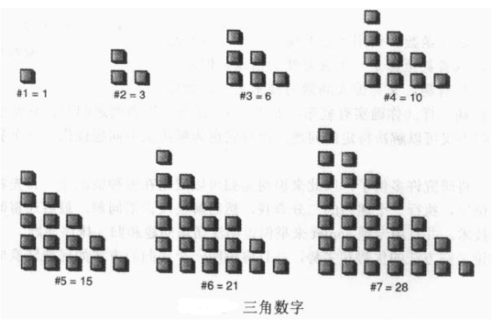
通过上面的图首先我们就可以想到使用循环来查找第n项的数值,下面代码就是从高度为n的列加到高度为1的列
int triangle(int n){ int total = 0; while(n>0){
total = total + n; --n;
} return total;
}上面方法循环了n次,第一次加n,第二次加n-1,一直加到1从而可以算出第n项的值。
使用递归的思想查找第n项的值,此时我们将三角数字看做是第一列和剩余所有列的和,如下图所示,可以写出triangle()方法
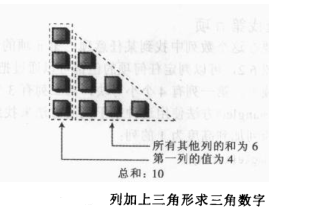
int triangle(int n){ //1. return (n + sumAllColums(n-1)) //这里我们可以发现sumAllColums方法做的事情和triangle做的事情一模一样
return (n + triangle(n-1)) //这里我们可以将上面步骤换为此步骤,从而得到求三角数字的递归算法}此时上面的递归代码是不会终止的,所以我们的每一个递归代码要有一个我们称之为基值(base case)以防止无限递归导致程序崩溃,所以上面求三角函数代码的基值就是1,
int triangle(int n){ if(n==1){ return 1; //求三角数字的基值
}else{ return (n+triangle(n-1)) ; //进行递归逻辑 }
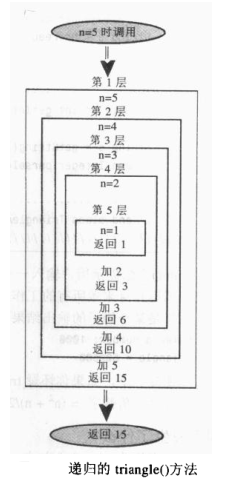
}下图表示了递归triangle方法的执行过程,假设传入n=5,从5开始每次减1,不断进入方法自身,直到减到1时,方法进行返回,直到返回到最外层。注意,在方法返回1之前,实际上同时有5个不同的triangle()方法实例存在,最外层传入的参数是5,最内层传入的参数是1
综上我们可以总结出递归方法的特征:
调用自身
调用自身为了解决更小的问题
存在足够简单的层次,即上面说的基值
递归的效率:递归的过程中控制必须从调用的位置转移到方法的开始处,除此之外这个方法的参数以及返回值会压入到一个内部栈中,从而知道访问的参数值和返回到哪里。所以递归效率较低,我们常常采用递归,是因为他从概念上简化了问题,而不是它更有效率。
II、归并排序
接下来我们讲讲与递归相关的排序算法,归并排序:
首先这种排序在时间上更有效,时间复杂度为O(N*logN),如果排序数据项N为10000,那么一般的简单排序N2就是100000000,而N*logN只是40000,意思就是若使用归并排序需要40s,那么使用插入排序需要近28小时。归并排序的缺点是需要在存储器中有另一个大小等于被排序的数据项数目的数组,所以排序对数组的大小有一定的限制。
归并算法的核心是归并两个已经有序的数组,我们假设数组A有4个数据项,数组B有6个数据项,他们要被归并到C中,开始的时候C有10个空的存储空间。下表显示了归并进行的必要的比较,每一次比较将较小的数据项复制到数组C中,表中B数组在第八步之后是空的,所以不需要再进行比较,直接将A数组复制到C中去即可。

接下来我们给出归并的java代码:
public int[] merge(int[] arrayA,int sizeA,int[] arrayB,int sizeB,int[] arrayC){ int aDex=0,bDex=0,cDex=0; //记录三个数组当前的脚标
while(aDex<sizeA&&bDex<sizeB){ //此时还需进行比较
if(arrayA[aDex] < arrayB[bdex])
arrayC[cDex++] = arrayA[aDex++]; else
arrayC[cDex++] = arrayA[bDex++];
} while(aDex<sizeA) //说明数组a中还有剩余数据,拷贝到数组c
arrayC[cDex++] = arrayA[aDex++]; while(bDex<sizeB) //说明数组b中还有剩余数据,拷贝到数组c
arrayC[cDex++] = arrayB[bDex++]; return arrayC;
}归并排序简单来讲就是反复地将数组进行分割,利用递归的思想,直到子数组只含有一个数据项(基值),在归并排序方法中每一次调用自身的时候排列都会被分成两部分,并且每一次返回时都会把两个较小的排列合并成一个更大的排列,接下来我们给出归并排序的代码:
public class DArray { private long[] theArray; //存储数据的数组
private int nElems; //填充数据个数索引
public DArray(int max) {
theArray = new long[max];
nElems = 0;
} /***插入数据*/
public void insert(long value){
theArray[nElems++] = value;
} /***归并排序的方法*/
public void mergeSort() { long[] workSpace = new long[nElems];
recMergeSort(workSpace, 0, nElems - 1);
} /**
* 利用递归进行归并排序
* @param workSpace 工作区
* @param lowerBound 归并区域的起始索引
* @param upperBound 归并区域的结束索引 */
private void recMergeSort(long[] workSpace, int lowerBound, int upperBound) { if (lowerBound == upperBound) { return;
} else { //找到中间分界点
int mid = (lowerBound + upperBound) / 2; //首先递归调用自己将前半部分的数据归并为有序 recMergeSort(workSpace, lowerBound, mid); //然后递归调用自己将后半部分的数据归并为有序
recMergeSort(workSpace, mid + 1, upperBound); //调用归并算法将上面归并有序后的数据进行归并
merge(workSpace, lowerBound, mid + 1, upperBound);
}
} /**
* 归并算法
* @param workSpace 工作区
* @param lowPtr 首段归并区域的初始索引
* @param highPtr 末端归并区域的初始索引
* @param upperBound 末端归并区域的结束索引 */
private void merge(long[] workSpace, int lowPtr, int highPtr, int upperBound) { int j = 0; //工作区的index
int lowerBound = lowPtr; //首段归并区域的初始索引(复制到theArray的初始索引)
int mid = highPtr - 1; //对应索引较小区域的结束位置索引
int n = upperBound - lowerBound + 1; //归并的此段区域所含有的数据项的个数 //将对应范围lowPtr到upperBound的数据复制到工作区
while (lowPtr <= mid && highPtr <= upperBound) { if (theArray[lowPtr] < theArray[highPtr]) {
workSpace[j++] = theArray[lowPtr++];
} else {
workSpace[j++] = theArray[highPtr++];
}
} //将对应还未复制完的数据复制到工作区中
while (lowPtr <= mid) {
workSpace[j++] = theArray[lowPtr++];
} while (highPtr <= upperBound) {
workSpace[j++] = theArray[highPtr++];
} //此步骤相当于是将对象内的theArray数组变成lowPtr到upperBound局部有序,将归并到工作区的数据放入theArray的对应位置
for (j = 0; j < n; j++) {
theArray[lowerBound + j] = workSpace[j];
}
}
}归并的效率:(假设复制和比较是最耗时的操作)
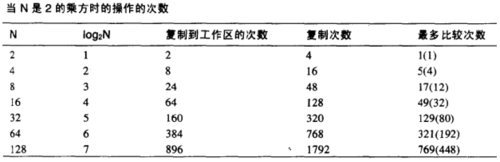
复制次数:
上表中可以看出来当N为2的乘方的时候的操作次数,我们可以这样来理解需要的复制次数,log2N表示将N对半分解为我们归并的基值1的时候需要的步数,然后每一步我们都需要将N个数据项复制到我们的工作区,所以复制到工作区的次数就应该是N*log2N,这些数据复制到工作区之后还需要复制到原数组中所以复制次数会增加一倍
比较次数:
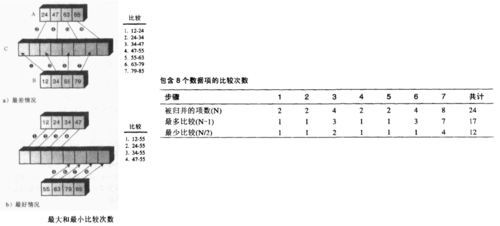
上图中我们可以前面表示进行归并的时候进行的最多和最少的比较次数,后表列举出了包含8个数据项进行归并排序的比较次数,对于八个数据项需要七次归并的操作,对于每一次归并最大比较次数是数据项减1,最小比较次数是数据项的一半,加在一起可算出归并排序需要的比较次数在12到17之间。
至此关于递归的思想,和关于递归的归并排序就结束了。



 随时随地看视频
随时随地看视频




