首先介绍一下动态规划:
动态规划(dynamic programming),我们称之为DP,是求最优解的一种很常见的方法。
思想和背包基本一样,如对背包感兴趣的可以移步 http://blog.csdn.net/sm9sun/article/details/53235986
两者都是保存局部各种状态下的最优解然后再构造最后所需的最优解。
通常处理DP问题,我们习惯于构造二维数组dp[i][j]
即dp[i][j]=f{ dp[i-1][0],dp[i-1][1]……}例如背包的dp[i][j]=fmax(dp[i-1][j],dp[i-1][j-b[i]*k]+a[i]*k);
如果把其看作一个树的话,即某节点最优解构造方法(状态转移方程)取决于上层的若干节点的最优解
满足动态规划的几个基本性质:
一、最优子结构:当前问题的最优解包含了子问题最优解
二、子问题重叠:所有的子问题都可以用一个算法计算(状态转移方程)
三、同级问题独立:同一级所有问题互不干涉,即a[i][j]的取值只能受a[i-1]及以上节点影响,绝对不受a[i][j-1],a[i][j+1]的影响。
我们以一道简单的例题说明一下
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=2084
题目描述:有如下所示的数塔,要求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?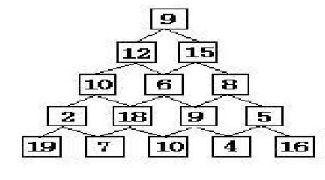
解题思路:当我们只看某一局部的话,很难做出正确的选择,如:顶部9该走12还是15呢? 或者底部,10该走18还是9呢?
那么我们以DP的思想看一下这个问题,因为是从顶端往下走的,所以叶子节点为19,7,10,4,16
我们看一下2这个节点,当我走到2时,我肯定会选择19,因为19大于7,那么我们可以把2当作21,因为当我走到2的时候,就意味着接下来会走到19,
照这个思路,我们可以把倒数第二层看作21,28,19,21。这就是我们所说的,最优子结构——当前问题最优解可以通过其子问题最优解计算得出
显然 我们的子问题重叠——状态转移方程为:a[i][j]=max{a[i][j]+a[i+1][j],a[i][j]+a[i+1][j+1]},并且,每一层取值至于上层有关,即满足同级问题独立
#include<stdio.h>int main(){ int a[200][200],i,j,t,n; scanf("%d",&t); while(t--) { scanf("%d",&n); for(i=1;i<=n;i++) for(j=1;j<=i;j++) scanf("%d",&a[i][j]); for(i=n-1;i>=1;i--) { for(j=1;j<=i;j++) { if(a[i+1][j]>=a[i+1][j+1]) a[i][j]+=a[i+1][j]; else a[i][j]+=a[i+1][j+1]; } }printf("%d\n",a[1][1]); }return 0;}这就是一道简单的DP问题,DP的问题有易有难,其难度在于我们是否能正确分析出子问题的状态转移方程,后续的几篇博客将继续说明DP相关的问题

 随时随地看视频
随时随地看视频




