1、 业务场景说明:
2、 从业务映射到机器学习:
3、 友商应用资料:
4、 LPA方法原理:[1][3]
5、 特征过滤的解决方案:[4]
6、 R语言试验
7、 总结(仅个人观点,欢迎指出错误):
附录:
一、常见的半监督学习大类:[2]
二、参考文献:
三、代码
1、 业务场景说明:
每个业务(或项目)期初阶段会面临一个问题:标签用户太少,未标签的用户太多。如:POI项目,X亿X千万的用户中只有X万不到的用户有过报错行为。如何快速将报错行为的人群快速扩散出去就成了现实业务问题。
2、 从业务映射到机器学习:
当Label<<unlabel时,传统的监督式学习在这种情况下效果明显下降。于是就有了“半监督学习”,半监督学习就是通过有限的label标签推广至unlabel标签数据的方法论。(具体可看附录相关文献。)
3、 友商应用资料:
目前还未查到相关资料,待补充(阿里,京东,百度,谷歌,facebook)
从百度学术或谷歌学术中可以看到一些大致的应用场景:
http://xueshu.baidu.com/s?wd=%E6%A0%87%E7%AD%BE%E4%BC%A0%E6%92%AD%E7%AE%97%E6%B3%95%E5%BA%94%E7%94%A8&tn=SE_baiduxueshu_c1gjeupa&ie=utf-8&sc_hit=1
4、 LPA方法原理:[1][3]
它是一种基于图的半监督学习方法,其基本思路是用已标记节点的标签信息去预测未标记节点的标签信息。利用样本间的关系建立关系完全图模型,在完全图中,节点包括已标注和未标注数据,其边表示两个节点的相似度,节点的标签按相似度传递给其他节点。
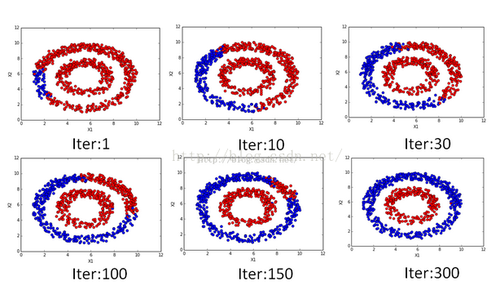
迭代过程如下:


图一,第一次迭代
图二,第二次迭代
第二次迭代原本没有传递信息的标签开始传递。
最终就会变成这样一个情况:(理想情况)
伪代码:
输入:user_id ,特征,tag
输出:user_id,相似值
1) 计算观测值与观测值的距离 dij 2) 计算传播权重 wij= 3) 计算传播概率 4) 创建标签矩阵F(标签为1标签为0的矩阵) 5) 执行传播:F=PF 6) 重置F中已知的标签 7) 重复步骤5)和6)到收敛。 8) 取相对分值最高的前N个数据 |
5、 特征过滤的解决方案:[4]
根据文档[4]具体方案如下:
组合使用缺失值比率、高相关滤波、方差滤波器:
缺失值20%认为该字段无法使用。
目前人为设定字段相关性>0.7为高相关,保留其中一个变量即可。
6、 R语言试验
输入:userid+特征+标签 (如果该userid无标签则填写0)
输出:userid+近似前N个的userid
实验使用数据为,历史使用过外卖用户与未使用过外卖用户。
实验方法:

指标如下:

实验:86个feature、限定正样本和负样本已知的情况下进行测试。测试结果如下:
注:24日频繁更新数据样本发现,该算法稳定性较弱(准确率最高79%,最低12%),受到训练样本的显示,如想要训练样本稳定需要使用大样本量。
正负样本配比为1:1实验结果:
2500个正样本测试2499个负样本测试 | 真实使用优惠券的用户数 | 真实未使用优惠券的用数 |
预测使用优惠券的用户数 | 2037 | 463 |
预测未使用优惠券的用户数 | 463 | 2036 |
精确率:81.5% 召回率:81.5%
注:因实验人为限定了预测前2500为1(正好等于样本数),所以会导致召回率=精确率。
正负样本比例为1:9实验二:
5000个训练集 500个正样本测试4499个负样本测试 | 真实使用优惠券的用户数· | 真实未使用优惠券的用数 |
预测使用优惠券的用户数 | 86 | 414 |
预测未使用优惠券的用户数 | 414 | 4585 |
精准率:17.2% 召回率:17.2%
随机更换数据 实验三:
500个正样本测试4499个负样本测试 | 真实使用优惠券的用户数· | 真实未使用优惠券的用数 |
预测使用优惠券的用户数 | 249 | 251 |
预测未使用优惠券的用户数 | 251 | 4748 |
准确率:50.2% 召回率:50.2%
7、 总结(仅个人观点,欢迎指出错误):
? 半监督学习有三个假设条件:[见附录论文]
1)Smoothness平滑假设:相似的数据具有相同的label。
2)Cluster聚类假设:处于同一个聚类下的数据具有相同label。
3)Manifold流形假设:处于同一流形结构下的数据具有相同label。
这就意味着当数据量小,或者关键feature选择偏离度较高时,模型的效能会大幅度下降。
? 后续需要优化的问题:
如何实施落地?目前单机测试最多进行10000*10000矩阵计算,(即支持1W人的距离矩阵。)如每次学习样本为5000人,那么训练样本的结果只能输出5000人的结果(计算时间约为2分钟,R写入本地MySQL数据需要5分钟)。
如何解决计算量大的问题?该算法需要计算完全部矩阵,最后进行相似性排名,取前N位为最有可能的用户。这就意味着如果要应用需要做一次大计算。
个人思路:
1、 利用集成,将数据分块化进行计算后合成最终结果。类似page rank 巨型矩阵解决方案[5]
2、 对于计算结果,不需要实时更新,做定期更新即可,节省资源。
3、 另可以将代码改为Python,方便日后实时。(python目前还不熟悉所以此次没有使用python,把代码模板附在了附录。有兴趣的同学可以一起研究一下)
? 前期可以使用该算法进行测试样本,有了样本积累后,可以转向全监督算法,提高预测准确率。
附录:
一、常见的半监督学习大类:[2]
1. self-training(自训练算法)
2. generative models生成模型
3. SVMs半监督支持向量机
4. graph-basedmethods图论方法
5. multiview learing多视角算法
二、代码
Python:http://scikit-learn.org/stable/modules/label_propagation.html
http://blog.csdn.NET/zouxy09/article/details/49105265
R LPA函数代码:
#dataframe 第一列为userid,最后1列为tag LPA<- function (dataframe,alpha,time) { dataframe<-as.matrix(dataframe) dataframe[which(is.na(dataframe))]<-0 #定义归一化函数(也可以用scale函数进行处理) min.max.norm <- function(x){ (x-min(x))/(max(x)-min(x)) } dataframe2<-apply(dataframe,2,min.max.norm) dataframe2[which(is.na(dataframe2))]<-0 distmatrix<-dist(dataframe2, method = "euclidean", diag = T, upper = T, p = 2)^2 Wmatrix<-exp(-distmatrix/(alpha^2)) Wmatrix<-as.matrix(Wmatrix)#构建权重矩阵 Wsum<-apply(Wmatrix,1,sum) Wmatrixnrow<-nrow(Wmatrix)#得到行数 Wmatrixncol<-ncol(Wmatrix)#得到列数 Wsum<-matrix(t(Wsum),nrow=Wmatrixnrow,ncol=Wmatrixncol) Pmatrix<-Wmatrix/Wsum#构建P矩阵 #装载F矩阵 F<-dataframe[,ncol(dataframe)] F<-as.data.frame(F) #记录标签F的行数,注意取数的时候有标签的数据在前面,无标签的数据在后面。 Fnrow=which(F==1,arr.ind=T)[,1] FF=F[Fnrow,] F<-as.matrix(F) for(i in 1:time){ F<-Pmatrix%*%F F[Fnrow,]<-FF } result<-cbind(dataframe[,1],F) colnames(result)<-c("user_id","P") return(result) } |
R 测试代码 使用的是本地mysql
#------------connet mysql------ library(RODBC); channel <- odbcConnect("lpa_test", uid="root", pwd=""); sqlTables(channel) lpa_waimaitest1=sqlFetch(channel,"lpa_waimaitest3") nrow(lpa_waimaitest1) lpa_waimaitest1[lpa_waimaitest1=="NULL"]<-0 lpa_waimaitest1[is.na(lpa_waimaitest1)]<-0 which(is.na(lpa_waimaitest1))#确保没有空值 which(lpa_waimaitest1=="NULL")#确保没有空值 lpa_waimaitest1$tag[5001:5500]<-0 #隐藏500个真实1值 reslut<-LPA(lpa_waimaitest1,1,1)#使用LPA算法 lpa_waimaitest1_reslut<-as.data.frame(reslut) #sqlSave(channel, lpa_waimaitest1_reslut, rownames = "state", addPK = TRUE)#上传结果 pre_waimai<-lpa_waimaitest1_reslut[order(lpa_waimaitest1_reslut[,2],decreasing = T),]#完成排序 pre_waimai<-cbind(pre_waimai,c(rep(1,5500),rep(0,4500)))#完成预测 lpa_waimaitest_yuan=sqlFetch(channel,"lpa_waimaitest3") test_result<-merge(pre_waimai,lpa_waimaitest_yuan[,c(1,ncol(lpa_waimaitest_yuan))],by="user_id") odbcClose(channel) test_result<-test_result[order(test_result[,2],decreasing = T),] test_zhunquedu<-test_result[test_result$P!=1,] gg<-table(predict=test_zhunquedu$`c(rep(1, 5500), rep(0, 4500))`,acutal=test_zhunquedu$tag) gg toufang<-paste0(round(gg[2,2]/sum(gg[,2]),4)*100,"%") fugai<-paste0(round(gg[2,2]/sum(gg[2,]),4)*100,"%") print(c("精准率:",toufang)) print(c("召回率:",fugai)) |
三、参考文献:
[1]陈文辉,基于图的半监督学习算法研究 http://www.docin.com/p-483916669.html
[2]半监督学习介绍 http://blog.csdn.Net/yhdzw/article/details/22733371
[3]标签传播算法 http://blog.csdn.net/zouxy09/article/details/49105265
[4] 为人称道的七种降维方法 http://dataunion.org/20803.html
[5] 用Map-reduce计算Page Rank(第6节) http://blog.jobbole.com/71431/

 随时随地看视频
随时随地看视频




