作者在这篇文章中介绍了一种新型的聚类算法 -- 基于密度的聚类算法。
灵感来源
经典的聚类算法K-means是通过指定聚类中心,再通过迭代的方式更新聚类中心的方式,由于每个点都被指派到距离最近的聚类中心,所以导致其不能检测非球面类别的数据分布。虽然有DBSCAN(density-based spatial clustering of applications with noise)对于任意形状分布的进行聚类,但是必须指定一个密度阈值,从而去除低于此密度阈值的噪音点。
这篇文章假设聚类中心周围都是密度比其低的点,同时这些点距离该聚类中心的距离相比于其他聚类中心最近。
聚类方法
对于每一个数据点i,需要计算两个量一个是局部密度 和与高于i点密度的最小距离。
和与高于i点密度的最小距离。
局部密度定义如下:

当x<0, ,否则
,否则 。这里
。这里 是一个截断距离,文中为所有点的相互距离中由小到大排列占总数2%的位置距离数值定义
是一个截断距离,文中为所有点的相互距离中由小到大排列占总数2%的位置距离数值定义 。算法只关心的量级因此对于的选择比较鲁棒。
。算法只关心的量级因此对于的选择比较鲁棒。
距离定义如下:

所有比i点密度高的所有点的最近距离表示 。对于最大密度的点其为所有点与点距离的最大值
。对于最大密度的点其为所有点与点距离的最大值 。
。
找出聚类中心:
以下A图为例,所有点的密度值按照由高到低排列,“1”表示密度最高的点。B图中画图每个点和的函数关系,从中可以看出“9”和“10”号点拥有相近的密度值但是其不同,这里“9”属于“1”号类别。“26”、“27”和“28”号点有一个相对较大的,但是其太小,这主要是因为它们是孤立点。 这里可以通过给定的 min和
min和 min筛选出同时满足(
min筛选出同时满足( >
> min)和(
min)和( >
> min)条件的点作为距离中心点。
min)条件的点作为距离中心点。

剩余点的类别指派:
当聚类中心确定之后,剩下的点的类别标签指定按照以下原则:
当前点的类别标签等于高于当前点密度的最近的点的标签一致。从而对所有点的类别进行了指定。如下图所示,编号表示密度高低,“1”表示密度最高,以此类推。“1”和“2”均为聚类中心,"3"号点的类别标签应该为与距离其最近的密度高于其的点一致,因此“3”号点属于聚类中心1,由于“4”号点最近的密度比其高的点为“3”号点,因此其类别标签与”3“号相同,也为聚类中心1。

在对每一个点指派所属类别之后,这里文章没有人为直接用噪音信号截断的方法去除噪音点,而是先算出类别之间的边界,然后找出边界中密度值最高的点的密度作为阈值只保留前类别中大于或等于此密度值的点,这里将此密度阈值记为 。
。
类别间边界确定:
以下图为例,对于类别1中的所有点,计算与其他类别中所有点距离小于等于的最大密度值,例如“1”号点由于其距离其他类别的点的距离均大于,因此不予考虑。由下图可以看出密度第6的值距离其他类别最近所以 =
= (6),由于“7”号点的密度
(6),由于“7”号点的密度 (7)<
(7)< , 因此将其作为噪音点去除,最后得到的类别1的点为绿色圈所示“1”、“3”和“6”。
, 因此将其作为噪音点去除,最后得到的类别1的点为绿色圈所示“1”、“3”和“6”。

聚类效果展示
下图是一个非球形类分布图,同时加入黑色噪音点后,A图为类的概率分布,B、C图为4000个和1000个样本点,E和F生成的每个点对应的 和
和 的函数图,可以明显看出类别中心及个数。F图为随着样本点的增加,错误指派点的比率。
的函数图,可以明显看出类别中心及个数。F图为随着样本点的增加,错误指派点的比率。

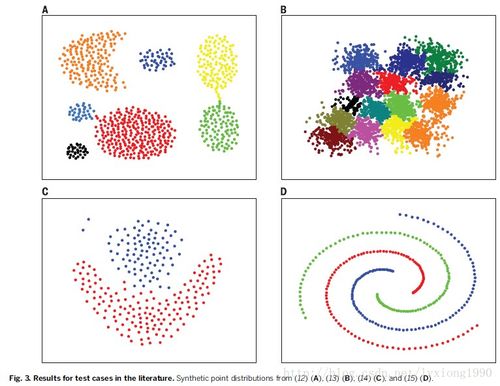
以下是使用该算法在其他数据集上进行聚类的效果图
算法优点
该聚类算法可以得到非球形的聚类结果,可以很好地描述数据分布,同时在算法复杂度上也比一般的K-means算法的复杂度低。
同时此算法的只考虑点与点之间的距离,因此不需要将点映射到一个向量空间中。
算法缺点
需要事先计算好所有点与点之间的距离。如果样本太大则整个距离矩阵的内存开销特别大,因此如果只需要得到最终聚类中心,则可以考虑牺牲速度的方式计算每一个样本点的 和
和 ,避免直接加载距离矩阵
,避免直接加载距离矩阵

 随时随地看视频
随时随地看视频




