matplot 画等高线图-原创手记-慕课网

matplot 除了可以画比较简单的图之外，还可以类似于等高线这样的图。在机器学习里面可以用于可视化分类的效果，比如在可视化svm分类的时候，就可以这样的方式去画图，在可视化上往往会有很好的效果。

代码如下：

import matplotlib.pyplot as plt 
import numpy as npdef f(x,y):
    # the height functions
    return 2 * x +y

n = 256# 将(-3,+3) 的这个区间分成256x = np.linspace(-3, 3, n)  # x shape (256,)y = np.linspace(-3, 3, n)  # y shape (256,)# np.meshgrid 形成一个平面网格，# X代表这个平面点的横坐标，Y代表这个平面点的纵坐标# X or Y shape is : (256, 256) # 这个函数的具体功能在下面讲X,Y = np.meshgrid(x, y)  

# 接下来进行颜色填充# 使用函数plt.contourf把颜色加进去，位置参数分别为：X, Y, f(X,Y)。plt.contourf(X, Y, f(X, Y))# 更多的参数，可以画出不同的风格，alpha=.75 表示透明度 ， cmap=plt.cm.hot 表示f(X,Y) 的值对应到color map的暖色组中寻找对应颜色#plt.contourf(X, Y, f(X, Y), 8, alpha=.75, cmap=plt.cm.hot)plt.show()

结果如下图：

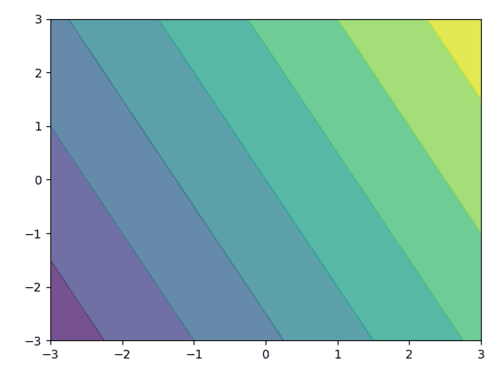
image.png

如果要画的点是离散的取值怎么办？
for example，画一个二维平面，上面的点的取值是离散的（比如说，0或1）。在机器学习经常需要可视化这样的东西，给一个平面，上面有很多点，有的属于正类，有的属于负类，那么如果可视化？

"""
画一个二维平面，上面的点的取值是离散的（比如说，0或1），
比如说机器学习经常需要可视化这样的东西，给一个平面，上面有很多点，有的属于正类，有的属于负类，那么如果可视化？

下面，是一个解决方案
"""import matplotlib.pyplot as plt 
import numpy as np


n = 10x = np.linspace(-3, 3, n)  
y = np.linspace(-3, 3, n)  


X,Y = np.meshgrid(x, y)# X,Y指的是一个 x 属于[-3,3],y属于[-3,3]的二维平面# z表示的是在这个二维平面内点的取值# np.random.randint(0,2,X.shape) 指的是生成一个shape形状的矩阵，里面的取值是0或1z=np.random.randint(0,2,X.shape)"""
rand = np.random.randint(0,2,(3,8))
print(rand)
 
[[1 1 0 0 1 0 1 0]
 [0 1 0 1 0 1 0 0]
 [0 0 1 0 0 1 0 0]]
"""plt.contourf(X, Y, z)
plt.show()

结果如下：

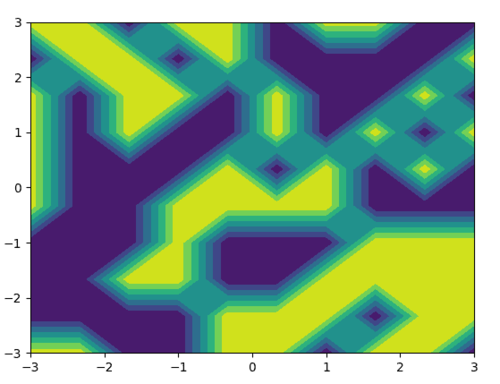
image.png

使用matplot画图的时候，常用的几个numpy函数：

np.meshgrid() 函数
一个简单的示例代码如下：

x = np.arange(-2,2)
y = np.arange( 0,3)   #生成一位数组，其实也就是向量x
Out[31]: array([-2, -1,  0,  1])

y
Out[32]: array([0, 1, 2])#将两个一维数组变为二维矩阵ret_x ,ret_y = np.meshgrid(x,y)  

# ret_x  可以理解为 x 纵向扩展ret_x  Out[36]: 
array([[-2, -1,  0,  1],
       [-2, -1,  0,  1],
       [-2, -1,  0,  1]])# ret_y 可以理解为 y 横向扩展ret_y Out[37]: 
array([[0, 0, 0, 0],
       [1, 1, 1, 1],
       [2, 2, 2, 2]])

如果我们想把一个平面上面，x 属于[-2,1]，y属于[0,2]的区域里面的点画出来。np.meshgrid（）就可以提供这样的功能。

它的返回值ret_x , ret_y 维度是相同的，分别表示了这个区域内点的横坐标和纵坐标。

np.c_ or np.r_ 函数
np.c_ or np.r_ 函数的作用是按行或者是按列合并向量

import numpy as np 

a = np.array([1,2,3])
b = np.array([5,2,1])# np.r_按row来组合array# a,b 必须是向量print (np.r_[a,b])# 输出# [1 2 3 5 2 1]# np.c_按colunm来组合arrayprint (np.c_[a,b])"""
# 输出
[[1 5]
 [2 2]
 [3 1]]
"""

举个例子：
svm 非线性核分类

"""
一个　非线性svm分类器　的demo
"""import numpy as npimport matplotlib.pyplot as pltfrom matplotlib import stylefrom sklearn import svm#style.use("ggplot")# 构造了一个非线性的数据X = np.array([[1,1],[5,5],[5,1],[1,5],[2.5,2.5],[2,3],[3,2],[2,2],[3,3]])
y = [1,1,1,1,0,0,0,0,0]
plt.scatter(X[:, 0], X[:, 1], c = y)#plt.show()#svc = svm.SVC(kernel='linear',C=1.0) # 线性核#svc = svm.SVC(kernel='rbf',C=1.0,gamma=1)  #如果是非线性核　可以还不同的gamma值svc = svm.SVC(kernel='rbf',C=1.0,gamma='auto')
svc.fit(X,y)

h = 0.01x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))


plt.subplot(1, 1, 1)
Z = svc.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired, alpha=0.8)

plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired)
plt.xlim(xx.min(), xx.max())
plt.title("SVC with kernel "+svc.kernel)
plt.show()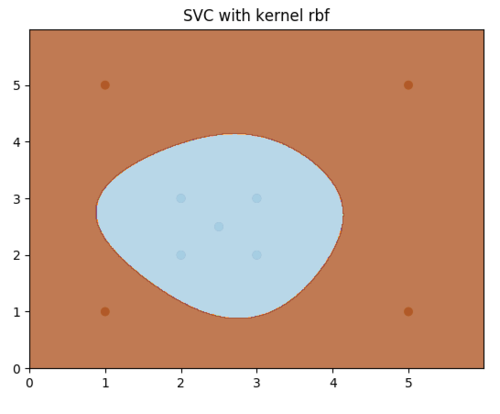

image.png

作者：爱秋刀鱼的猫

链接：https://www.jianshu.com/p/0e11ecf0c0b6