python 利用递归实现全排列

使用递归实现全排列。123实现全排列！
法1：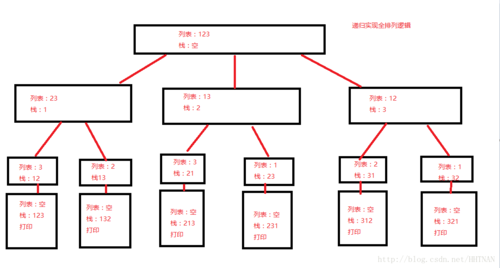

上面定义了两个列表，一个列表存的是需要全排列的数据，另一个列表是当做栈来用的，可以把这个递归想成一棵树，在最顶端是包含所有值得列表，之后从这个列表中循环拿掉一个值，到了第二层，这时候栈里面存放的就是拿出来的那个数据，这一层的一个值里面就少了刚刚拿掉的值，一直到最后这个列表为空的时候，栈里面存的就是这个排列的结果，

#!/usr/bin/env python# encoding:utf-8def perm(list,stack):
    if not list:
        print(stack)  # 到树的最后，输出结果
    else:  # 没有到树的叶子节点的时候，使用递归继续往下找。
        for i in range(len(list)):
            stack.append(list[i])            del list[i]
            perm(list,stack)
            list.insert(i,stack.pop())

list=[1,2,3]
stack=[]
perm(list,stack)

同时在python中有一个模块叫做itertools，使用这个模块能够快速的求解排列组合问题
OK，这样理解起来是不是容易多了，这样也能够解释为什么递归其实就是一棵树了。。。当然，也可以使用栈来代替递归实现，不过。。。目前还没实现。区别差不多就是树的递归遍历和非递归遍历的区别吧。
法二、
排列：从n个元素中任取m个元素，并按照一定的顺序进行排列，称为排列；
全排列：当n==m时，称为全排列；

比如：集合{ 1,2,3}的全排列为：
{ 1 2 3}  
{ 1 3 2 }
{ 2 1 3 }
{ 2 3 1 }
{ 3 2 1 }
{ 3 1 2 }

递归思想：
取出数组中第一个元素放到最后，即a[1]与a[n]交换，然后递归求a[n-1]的全排列

1）如果数组只有一个元素n=1，a={1} 则全排列就是{1}
2）如果数组有两个元素n=2，a={1,2} 则全排列是：
{2,1}–a[1]与a[2]交换。交换后求a[2-1]={2}的全排列，归结到1)
{1,2}–a[2]与a[2]交换。交换后求a[2-1]={1}的全排列，归结到1)
3）如果数组有三个元素n=3，a={1,2,3} 则全排列是
{{2,3},1}–a[1]与a[3]交换。后求a[3-1]={2,3}的全排列，归结到2）
{{1,3},2)–a[2]与a[3]交换。后求a[3-1]={1,3}的全排列，归结到2）
{{1,2},3)–a[3]与a[3]交换。后求a[3-1]={1,2}的全排列，归结到2）
…
依此类推。
利用python实现全排列的具体代码perm.py如下：

OUNT=0  def perm(n,begin,end):  
    global COUNT  
    if begin>=end:  
        print n  
        COUNT +=1  
    else:  
        i=begin  
        for num in range(begin,end):  
            n[num],n[i]=n[i],n[num]  
            perm(n,begin+1,end)  
            n[num],n[i]=n[i],n[num]  

n=[1,2,3,4]  
perm(n,0,len(n))  
print COUNT

[参考连接]【1】
       【2