在纳米比亚的 PyCon 会议上,我发表了一篇名为 《使用 Python 解决“升级版的剪刀石头布”》(Rock, Paper, Scissors, Lizard, Spock with Python )的文章。在这篇文章中,介绍到用Nashpy 来计算两个玩家的平衡是很简单的事情,但是其中只是涉及了一点点演化稳定性的内容。 在这篇博文中,我将阐述一下如何在 Python + Numpy 环境下,使用大概 40 行代码来建立一个简单的演化过程模型。
我想讲的第一个游戏是“旅行者困境”问题。这里给出一个简化的版本:

我不想过多的讲解这个游戏的数学模型如何建立。在建模后,我们只需要知道一件事情,那就是我们有两个玩家:
行玩家:选择我们处于哪一行;
列玩家:选择我们处于哪一列。
如果,行玩家选择的是第二行,列玩家选择的是第三列,则得分为: 5,1。即行玩家得 5 分,而列玩家得 1 分。这个时候列玩家可能会倾向于选择第一列,这样的话得分就是 0,4 了。
下面,我们可以使用 Nashpy 来计算这个游戏的平衡位置。

我们可以看到,纳什平衡是由两个向量组成的单个集合,向量表明了玩家应该如何玩这个游戏:
行玩家应该按照 [1,0,0] 来玩
列玩家也应该按照 [1,0,0] 来玩
在这里,[1,0,0] 是概率向量,表示一个玩家的游戏策略的概率。所以,在这种情况下,两位玩家都应该选择第一个选择,这样的话得分为 2,2。这位置称为纳什平衡,因为所有玩家都不能偏离这个点(一旦偏离,就可能得到比别人低的分数)。
我们可以对“升级版的剪刀石头布”这个游戏进行同样的建模,其数学模型如下:
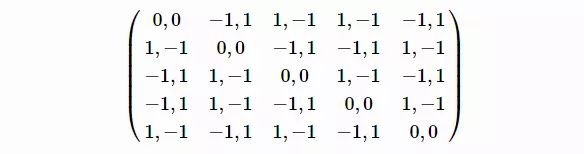
接下来,使用如下的程序计算其纳什平衡:

我们可以看到每个位置都是 1/5 的概率,所以两位玩家可以随意的选择。这完全可以凭借个人直觉,因为当两位玩家都这么做的时候,实际上就是随机不可预测的。
所有结果都很合理。纳什平衡是博弈论中一个很有用且很重要的概念,但是当我们以演化的视角看这些游戏的时候,会发生什么呢?
如果我们有一大群人,并且这群人总是会选择与他们人数相同的多种选择。他们每个都和另外一大群人玩这个游戏,如果他们比对手得分要高,他们继续。反之则他们的对手继续。
下面是我们使用 Python 和 Numpy 来进行模拟的代码。
首先,得到一个随机的人数:

然后开始游戏:

接下来进行变化(将那些获胜的策略进行汇总):

最后将上面的这些进行汇总,给定一个游戏的迭代次数,重复的运行 mutate 函数:

下面让我们看看最后画出来的曲线图(点击这里下载 Jupyter notebook)
首先我们看看玩“旅行者困境”这个游戏时会发生什么(回顾上面讲的纳什平衡,两位玩家应该选择第一种策略):

我们可以看到,人群中的玩家很快都选择了第一种策略。当然这也可能是我们使用了特定的随机数种子所引起的人为结果。下面的图片展示了使用不同的随机数种子所得到的结果图片。

他们的初始条件皆不相同但是结果相同:人群中的人们使用都是纳什平衡策略。
接下来的是比较酷的一部分了,让我们看看在“升级版的剪刀石头布”的曲线图中会发生了什么:

我们可以看到结果不是很稳定。下面的图片显示了不同随机数种子的结果:

关于两者稳定性的差异有个直观的解释:在“旅行者困境”游戏中纳什平衡策略是非常强的:如果每个人都按照纳什平衡来决策,我们就没法作出改变,我们只能跟别人一样。在“升级版的剪刀石头布”游戏中:如果每个人都是随机的玩,或者所谓的人群是由玩家或者策略进行随机的组合,你就很有可能碰见那些战胜你的人。
从这篇文章中,我们有两点需要注意:
这只是使用 Python 模拟一个简单的演化过程。
人数的动态变化为这个游戏添加了一个迷人的维度。我在这里使用的演化过程非常的简单,一般情况都是使用马尔科夫随机过程来研究这类问题。你也可以使用 Python 的库来研究这类“囚徒困境”问题,使用的库的链接为: axelrod.readthedocs.io/en/latest/tutorials/getting_started/moran.html
英文原文:http://vknight.org/unpeudemath/mathematics/2017/03/08/simple-evolutionary-process.html

 随时随地看视频
随时随地看视频




