什么是哈夫曼树呢？
哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树。下面用一幅图来说明。
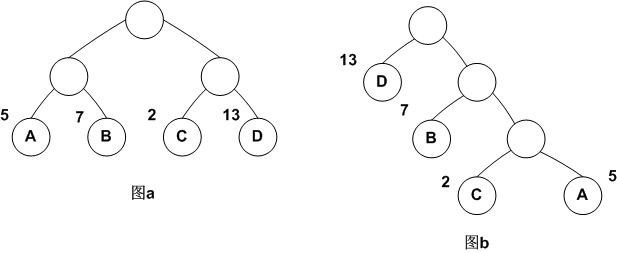
它们的带权路径长度分别为：
图a： WPL=5*2+7*2+2*2+13*2=54
图b： WPL=5*3+2*3+7*2+13*1=48
可见，图b的带权路径长度较小，我们可以证明图b就是哈夫曼树(也称为最优二叉树)。
哈夫曼编码
用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径，对路径上的各分支约定指向左子树的分支表示”0”码，指向右子树的分支表示“1”码，取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码，即是哈夫曼编码。
就拿上图例子来说：
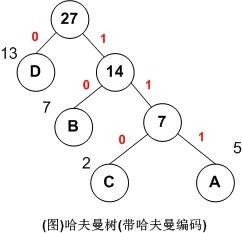
A，B，C，D对应的哈夫曼编码分别为：111，10，110，0
用图说明如下：
随时随地看视频
