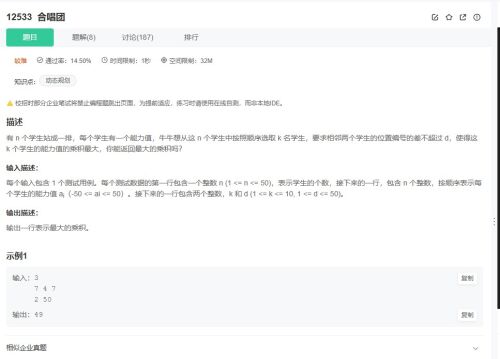
一、题目解读
牛客12533题要求从n个人中选择k个人,使他们的能力值乘积最大,且相邻两人编号差不超过d。需考虑正负数的乘积组合情况,通过优化算法找到最优解。
二、解题思路
采用动态规划(Dynamic Programming)解决。定义二维数组dp_max[i][j]和dp_min[i][j],分别表示选j个人且最后一个人为i时的最大和最小乘积。通过状态转移方程,利用前j-1个人的乘积与当前能力值计算,兼顾正×正、负×负、正×负三种情况,避免重复计算。
三、解题步骤
1. 初始化:选1人时,乘积即其能力值。
2. 循环处理选j个人(2≤j≤k),当前人i从j到n遍历。
3. 前一个人l在[i-d, i-1]范围内,计算最大/最小乘积:
○ dp_max[i][j] = max(dp_max[l][j-1] * ability[i-1], dp_min[l][j-1] * ability[i-1])
○ dp_min[i][j] = min(dp_max[l][j-1] * ability[i-1], dp_min[l][j-1] * ability[i-1])
4. 最终结果:遍历dp_max[k][i](i=k到n)取最大值。
四、代码与注释
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
long long maxProduct(int n, vector<int>& ability, int k, int d) {
// dp_max[i][j]表示选j个人,最后一个人是i时的最大乘积
// dp_min[i][j]表示选j个人,最后一个人是i时的最小乘积
vector<vector<long long>> dp_max(n+1, vector<long long>(k+1, LLONG_MIN));
vector<vector<long long>> dp_min(n+1, vector<long long>(k+1, LLONG_MAX));
// 初始化:选1个人时就是自己的能力值
for(int i = 1; i <= n; i++) {
dp_max[i][1] = ability[i-1];
dp_min[i][1] = ability[i-1];
}
for(int j = 2; j <= k; j++) { // 选j个人
for(int i = j; i <= n; i++) { // 当前选第i个人
// 前一个人只能在[i-d, i-1]范围内
int start = max(j-1, i-d); // 至少需要j-1个人
for(int l = start; l < i; l++) {
// 考虑三种情况:正×正,负×负,正×负
dp_max[i][j] = max(dp_max[i][j], max(dp_max[l][j-1] * ability[i-1], dp_min[l][j-1] * ability[i-1]));
dp_min[i][j] = min(dp_min[i][j], min(dp_max[l][j-1] * ability[i-1], dp_min[l][j-1] * ability[i-1]));
}
}
}
// 找出选k个人时的最大乘积
long long result = LLONG_MIN;
for(int i = k; i <= n; i++) {
result = max(result, dp_max[i][k]);
}
return result;
}
int main() {
int n, k, d;
cin >> n;
vector<int> ability(n);
for(int i = 0; i < n; i++) cin >> ability[i];
cin >> k >> d;
cout << maxProduct(n, ability, k, d) << endl;
return 0;
}五、总结
本解法通过动态规划将复杂问题分解为子问题,利用状态转移优化时间复杂度。关键在于处理正负数的乘积逻辑,确保最终结果正确。代码结构清晰,注释明确,适用于同类最大乘积问题的参考与学习。
来源:牛客网题解

 随时随地看视频
随时随地看视频




