交叉熵损失函数简介

一个常用的损失函数介绍

在机器学习中，选择合适的损失函数对有效模型训练至关重要。交叉熵损失已成为一种流行的和强大的选择，适用于任何可以被表述为从多个可能类别中预测单个标签的任务，也就是多类分类，它提供了一个平滑且可微的优化目标。本文尽量用简单易懂的方式解释这些关键概念。

由Bing 图像创作器 制作，使用提示词“带有对损失函数感知的机器人”

交叉熵损失是一种量化模型预测与实际结果匹配程度的机制，奖励模型在正确答案上分配更高的概率。由于使用了对数函数，交叉熵损失对高置信度预测的变化更加敏感。这间接促使模型在不确定时更加谨慎，而不是自信地犯错。

关键是这样的想法。

• 模型预测正确的信心越高，损失就越低。
• 模型越自信地预测错误，损失也就越大。

对于一个包含K个类别的多类别分类问题，我们可以表示单一样本的交叉熵损失如下：

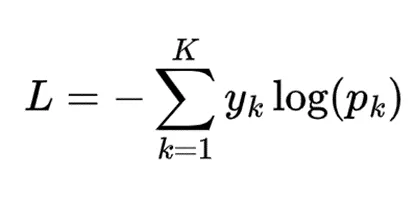
此处：

• y_k 是类别标签 k 的真实概率，通常用 1 表示正确类别，用 0 表示其他所有类别。
• p_k 是类别标签 k 的预测概率

这些属性共同作用，使得模型对正确的类别给出高概率，对错误的类别给出低概率，并且在高置信度预测上特别敏感。

特别地，这个损失函数有几个关键的属性，使其特别适合训练分类模型。

• 增强对正确答案的信心：对于正确类别（其中 y_k = 1），损失项 -log(p_k) 随着 p_k 的增大而减小。这促使模型给正确类别分配更高的概率。
• 惩罚错误：虽然不正确的类别不会直接对损失计算做出贡献，但该函数隐含地惩罚错误。增加不正确类别概率的同时，必须相应地减少正确类别的概率（因为概率之和必须为 1），从而增加整体损失。
• 对数尺度敏感性：对数函数使高概率的变化比低概率的变化对损失的影响更大。例如，将预测从 0.98 提升到 0.99 比从 0.51 提升到 0.52 更大幅度地减少了损失。
• 处理不确定性：损失不会像对待自信的错误预测那样严厉地对待不确定性（均匀分布的概率）。这源于对数行为：从不确定状态到自信的正确预测减少损失，而从不确定状态到自信的错误预测则增加损失。

在训练过程中，模型会调整其参数设置以最小化损失，学会输出与训练数据中的真实类别分布非常接近的概率分布。通过这种方式，较大的偏差会得到更强的信号，帮助模型随着时间推移更加准确地预测。

一个计算的例子

我们来看一个例子来说明交叉熵是怎么算的。

假设我们有一个三分类问题（比如，将一张图片识别为狗、猫或鸟）。对于单个样本：

• 标签：[1, 0, 0]（正确的答案是“狗”）
• 预测的概率：[0.7, 0.2, 0.1]（70%的几率是狗，20%是猫，10%是鸟）

对于这个样本来说，交叉熵损失值会是：。

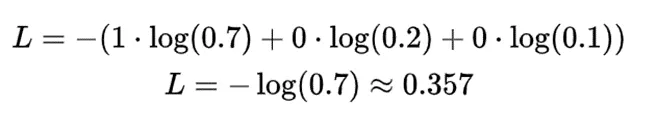
那么，如果模型更确定（例如 [0.9, 0.05, 0.05]，），损失值会更低：

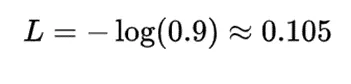
反之，如果模型错误预测了并且很有信心（例如，[0.1, 0.8, 0.1]），损失会非常高：

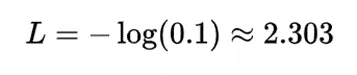
从这个例子中，我们可以开始体会到交叉熵损失是如何通过奖励正确预测和惩罚错误预测的方式来运作的，特别是对于那些高置信度的错误预测，惩罚会大幅度增加。

从logit到概率的转换

我们的预测通常以 logits 形式给出，即神经网络最后一层的原始、未归一化的输出。这些 logits 实际上是输入到最后一层的线性组合，因此不具备概率意义。

为了把这些转换成概率，通常会应用SoftMax函数，该函数保持输入间的相对顺序，并放大大的输入之间的差异，同时确保输出的总和为1。

softmax函数定义为

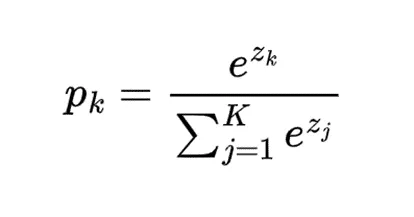
这里 z_k 是类别 k 的 logit（原始输出）。

值得注意的是，因为分母的规范化，增加一个logit会降低其他类别的概率值。这与我们的直觉一致，也就是说，当模型对某个类别更有信心时，它对其他类别就不太自信了。

在我们的交叉熵表达式中，包括 SoftMax (公式)，我们就可以得到：

影响权重调整的因素

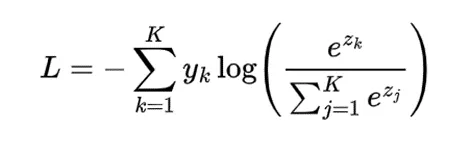
交叉熵损失对每个得分的梯度为：

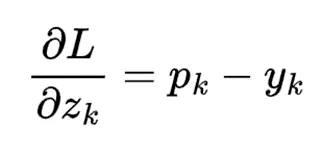
简单梯度形式来源于SoftMax函数的指数性质与交叉熵中的对数相互抵消的结果。此梯度可用于指导权重的更新，具体方法如下。

权重调整方向由 p_k 减 y_k 的结果是正还是负来决定。

• 如果 $p_k > y_k$，模型高估了概率，我们就降低相关权重。
• 如果 $p_k < y_k$，模型低估了概率，我们就提高相关权重。

|p_k — y_k|的绝对值大小决定了调整权重的多少。

• 差异越大，更新越大。
• 随着预测的改善，|p_k — y_k| 变小了，自然地使更新变慢。

所以

• 对于正确的类别（其中 (y_k = 1)），梯度会将类别 k 的洛吉特 (z_k) 提高。
• 对于不正确的类别（其中 (y_k = 0)），梯度会将类别 k 的洛吉特 (z_k) 降低。
• SoftMax 函数确保增加一个概率会降低其他概率。

集成交叉熵损失的实现

我们现在已经讨论了交叉熵损失的理论部分，接下来让我们来看看它在实践中是如何被实现的，特别是在流行的深度学习框架中，比如 PyTorch。

PyTorch 实现多分类任务

PyTorch实现的交叉熵损失函数与我们之前讨论的公式非常相似，但针对效率和数值稳定性做了优化。

在PyTorch的nn.CrossEntropyLoss中，主要区别在于

• 直接操作原始"logits"，而不是概率。这种转换是通过内部的"log-softmax"操作来处理，随后是"负对数似然损失"，从数学的角度来看与我们之前的公式等价。

• 目标标签应为类别索引，而不是"one-hot"编码的向量。

对于一个样本，可以分为两个步骤。

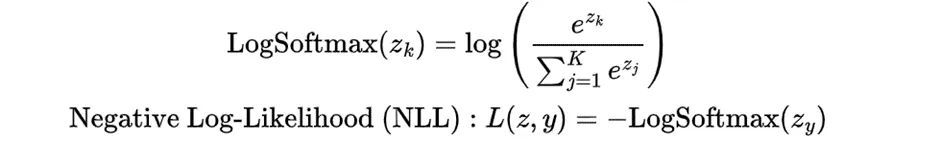
把这些步骤合在一起，我们就得到：

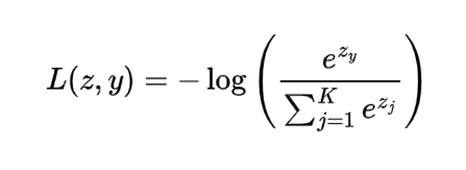
此处:

• K 表示类别的数量
• z 是单一样本的 logits（预测每个类别的分数）
• y 是该样本的真实类别

对于 N 个样本的一批，PyTorch 分别计算每个样本的损失，然后再进行平均值计算。

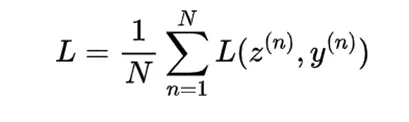
这里，z^n 和 y^n 分别表示批次中第 n 个样本的 logits（通常指未经过softmax处理的预测值）和真实类别索引。

这种先应用Log SoftMax再使用NLL的两步法能提供更好的数值稳定性和计算效率，特别是在处理大量类别的情况下。

二进制交叉熵损失

在二元分类中，当只有两个类别时，交叉熵损失公式可以被简化。以下是多个样本在二元分类中简化后的样子。

地点：

• L_{total} 是所有样本的总损失值
• N 是样本的数量
• y_n 是样本 n 的真实标签（0 或 1，代表两个类别）
• p_n 是样本 n 的正类（即类别 1）的预测概率

与多类公式相比，不同的地方在于：

• 由于只有两类，我们不需要对K求和。
• 我们利用互补的概率，用p_n表示类别1的概率，1-p_n表示类别0的概率，因为总概率必须为1。
• 我们不再用y_k来表示每个类别的真实概率，在二分类问题中，用1表示正类，0表示负类。
• 我们显式地包含正类和负类的项，分别为y_n log(p_n)和(1-y_n) log(1-p_n)。

这个二元交叉熵损失函数对于两类问题更简洁且计算效率更高，在 K=2 的情况下，它在数学上等价于多类问题的公式。模型通常只需输出正类的概率 ( p_n )，而负类的概率则隐含为 ( 1-p_n )，这样就无需单独输出了。

结论部分

希望这帮助你理解交叉熵损失是如何工作的直觉，并帮助指导优化时权重调整。