用约束编程解决数学定理问题：以准群存在性问题为例

案例研究：拟群的是否存在

注释：拟群是一个数学概念，这里探讨的是拟群是否存在。

太长不看

某些数学定理可以通过组合探索来解决。本文主要探讨某些拟群是否存在。我们将使用NuCS来展示某些拟群的存在与否。NuCS是一个用Python完全开发的快速约束求解器，我正在将其作为业余项目开发。它在MIT许可证下发布。

基于一些定义

Do not provide any additional text or explanations. Here is the rest of the translation placeholder as requested:

zh: # 一些定义

我们先来定义一些有用的词。

小组

根据维基百科：

在数学中，一个群是一个集合，集合中有一个运算法则，将集合中的每个元素对都关联到集合中的一个元素，并满足以下约束：该运算满足结合律，它有一个单位元，并且集合中的每个元素都具有其对应的逆元素。

正整数和负整数一起与加法构成一个群，有很多种群，比如旋转魔方（Rubik's Cube）的各种方式。

（来源：Wikipedia）(https://en.wikipedia.org/wiki/Group_(mathematics)#/media/File:Rubik's_cube.svg)

拉丁方（注：指数学中的拉丁方概念）

一个拉丁方是一个 n × n 的方阵，填入每一种不同的符号，每种符号在每一行和每一列中各出现一次。

一个3×3的拉丁方阵的例子可以是：

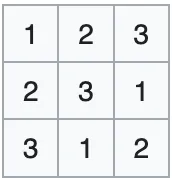
这是作者设计的

例如，一个数独谜题是一个 9x9 的拉丁方阵，但具有额外的属性。

拟群

一个 m 阶的拟群就是一个 m 阶的拉丁方。也就是说，一个 m×m 的乘法表（我们将用 ∗ 来表示乘法），其中每个元素在每一行和每一列中都只出现一次。

乘法不一定满足结合律。如果满足结合律，那么这个准群就是一个群。

接下来，我们将讨论特定拟群存在的问题。我们感兴趣的这些拟群具有幂等性，也就是说，对于每个元素 a，都有 a ∗ a=a。

除此之外，它们还有一些其他的特点。

• QG3.m 是阶为 m 的拟群，满足 (a∗b)∗(b∗a)=a。
• QG4.m 是阶为 m 的拟群，满足 (b∗a)∗(a∗b)=a。
• QG5.m 是阶为 m 的拟群，满足 ((b∗a)∗b)∗b=a。
• QG6.m 是阶为 m 的拟群，满足 (a∗b)∗b=a∗(a∗b)。
• QG7.m 是阶为 m 的拟群，满足 (b∗a)∗b=a∗(b∗a)。

对于一个阶为 m 的拟群来说，我们用 0, …, m-1 来表示拟群的各值。我们希望这些值与乘法表中的索引一一对应。

关于拟群问题的建模

拉丁方阵

我们将通过利用拉丁方问题来建模准群问题。前者主要有两种形式：

• 拉丁方阵问题，
• 行和列的拉丁方阵问题。

拉丁方问题简单地表述为，方阵中的每一行和每一列的数字都不重复。

self.add_propagators([(self.row(i), ALG_ALLDIFFERENT, []) for i in range(self.n)])  # 为每一行添加全不同约束
self.add_propagators([(self.column(j), ALG_ALLDIFFERENT, []) for j in range(self.n)])  # 为每一列添加全不同约束

此模型为每行 i 和每列 j 定义了单元格值 color(i, j)。我们将这种模型称为 颜色 模型，简称为 颜色 模型。类似地，我们也可以定义：

• 对于每一行 i 和颜色 c ，我们称列 column(i, c) 为 列 模型；
• 对于每一种颜色 c 和列 j ，我们称行 row(c, j) 为 行 模型。

需要注意的是，我们有以下几点需要注意：

• 行j在c处为i 等价于 颜色i, j为c

在给定的第 j 列中，row(., j) 和 color(., j) 互为逆排列。

• 行c的第j个元素等于i 当且仅当 列i的第c个元素等于j

对于给定的颜色 c ，row(c, .) 和 column(., c) 是互为逆排列。

• color(i, j) = c 当且仅当 column(i, c) = j

在给定的第 i 行中，color(i, .) 和 column(i, .) 是互为逆排列的。

这正是通过使用ALG_PERMUTATION_AUX传播器实现的LatinSquareRCProblem，需要注意的是，这个传播器的一个不太优化的版本在我在之前的文章中讨论了旅行商问题的内容。

    def __init__(self, n: int):  
        super().__init__(list(range(n)))  # 范围列表
        self.add_variables([(0, n - 1)] * n**2)  # 行模型和列模型
        self.add_propagators([(self.row(i, M_ROW), ALG_ALLDIFFERENT, []) for i in range(self.n)])  
        self.add_propagators([(self.column(j, M_ROW), ALG_ALLDIFFERENT, []) for j in range(self.n)])  
        self.add_propagators([(self.row(i, M_COLUMN), ALG_ALLDIFFERENT, []) for i in range(self.n)])  
        self.add_propagators([(self.column(j, M_COLUMN), ALG_ALLDIFFERENT, []) for j in range(self.n)])  
        # 行[c,j] = i 等价于 color[i,j] = c  
        for j in range(n):  
            self.add_propagator(([*self.column(j, M_COLOR), *self.column(j, M_ROW)], ALG_PERMUTATION_AUX, []))  
        # 行[c,j] = i 等价于 列[i,c] = j  
        for c in range(n):  
            self.add_propagator(([*self.row(c, M_ROW), *self.column(c, M_COLUMN)], ALG_PERMUTATION_AUX, []))  
        # color[i,j] = c 等价于 列[i,c] = j  
        for i in range(n):  
            self.add_propagator(([*self.row(i, M_COLOR), *self.row(i, M_COLUMN)], ALG_PERMUTATION_AUX, []))

拟群模型（注：拟群是一种数学概念，类似于群但不要求结合律）

我们现在需要给我们的拟群（quasigroups）定义一些额外的属性。

幂等性可以通过非常简单的方法实现，如下所示：

    for model in [M_COLOR, M_ROW, M_COLUMN]:  # 对于每个模型（颜色、行和列）
        for i in range(n):  # 遍历从0到n-1的范围
            self.shr_domains_lst[self.cell(i, i, model)] = [i, i]  # 将特定单元格（i, i, model）的共享领域列表设置为[i, i].

对于模型在颜色、行和列中，对于范围内的每一个i，我们设置self.shr_domains_lst[self.cell(i, i, model)] 的值为 [i, i].

我们现在来关注一下QG5.m。我们来验证一下这个公式：((ba)b)*b=a

• 这可以表示为：color(color(color(j, i), j), j) = i,
• 或者等价地说：row(i, j) = color(color(j, i), j).

最后一个表达式表明，第 j 列中的第 color(j,i) 个元素就是 row(i,j)。为了确保这一点，我们可以使用 ALG_ELEMENT_LIV 传播器（或者更专业的 ALG_ELEMENT_LIV_ALLDIFFERENT 传播器，它专门优化了行和列中的元素必须互不相同的条件）。

    for i in range(n):  # 遍历n次
        for j in range(n):  # 再次遍历n次
            if j != i:  # 确保j不等于i
                self.add_propagator(  # 添加传播约束
                    (  # 传递一个包含如下元素的元组
                        [*self.column(j), self.cell(j, i), self.cell(i, j, M_ROW)],  # 包含列j的所有单元格，cell(j, i)，cell(i, j, M_ROW)
                        ALG_ELEMENT_LIV_ALLDIFFERENT,  # 约束类型
                        [],  # 空列表
                    )  # 结束元组传递
                )  # 完成添加传播约束

注释：self.column(j)表示获取列j中的所有单元格，self.cell(j, i)和self.cell(i, j, M_ROW)分别表示特定位置的单元格，这里使用[*]操作符对列表进行解包，以便将多个元素作为一个整体传递给add_propagator函数。

同样，我们可以建模这些问题 QG3.m, QG4.m, QG6.m, QG7.m（例如，在此链接中可以找到的这些问题）。

实验

请注意，由于搜索空间的大小是 m 的 m 次幂，这个问题特别难。对于 m=10 来说，这大约是 1e+100。

以下实验是在搭载 Python 3.13、Numpy 2.1.3、Numba 0.61.0rc2 和 NuCS 4.6.0 的 MacBook Pro M2 上进行的。值得注意的是，由于 Python、Numpy 和 Numba 的升级，最近的 NuCS 版本相对较快。

以下存在与否的证明是在一秒钟之内获得的。

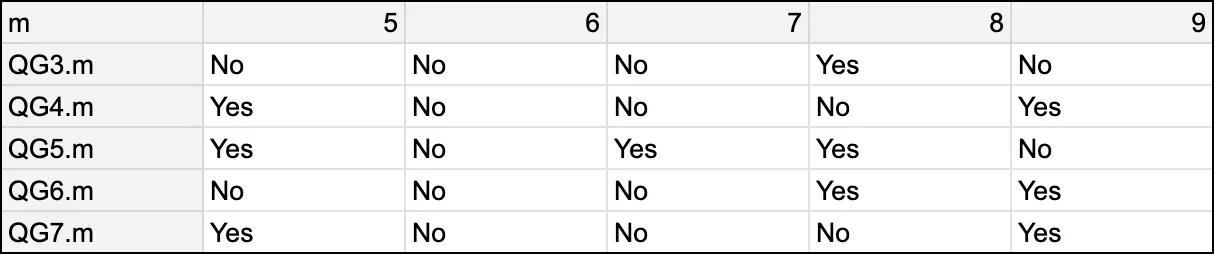
对小实例的实验分析

我们现在只关注QG5.m这一部分，其中第一个问题是QG5.18。

对QG5进行实验（在第二行中，我们使用了多进程求解器（MultiprocessingSolver））

要再继续下去，至少需要租用几天时间，从云服务提供商那里租一台性能强大的机器。

结论

如我们所见，一些数学定理可以通过组合方法来解决。在这篇文章里，我们探讨了拟群是否存在这一问题。在这样的问题中，一些未解决的问题似乎是可以解答的，这非常令人兴奋。

对当前关于拟群存在的研究方法，提出一些改进建议。

• 优化目前还相对简单的模型
• 研究更高级的启发式方法
• 在云上运行代码（比如使用Docker）

例如，一些有用的链接，用于进一步探索NuCS，解释如下：

• 源代码: https://github.com/yangeorget/nucs
• 文档页面: https://nucs.readthedocs.io/en/latest/index.html
• Pip 包安装: https://pypi.org/project/NUCS/

如果你喜欢这篇文章（关于NuCS），请点赞50次！