在扩散模型中,噪声会在前向过程中加入,随时间推移在反向过程中被消除。因此,时间步长信息非常重要,必须被纳入网络中。
所以我们怎么才能把时间信息加到网络里呢?一个简单的方法是在输入特征中添加时间步长 T ,例如 [inputFeature , T](如 [输入特征, 时间步T])。我用这个方法弄了一个简单的扩散模型。我已经用这种方法实现了个简单的扩散模型。
然而,这种方法也有一些缺点。如果在训练和推理时时间步不同,它就不太能适应不同的情况了。例如,如果一个模型是在时间步为50时训练的,那么在推理时时间步为10000时,模型的准确性可能就不太好了。
所以要不我们试试将时间步长的范围规范化?例如,如果我们把范围设为0到1,所有的时间步长都将落在0到1的范围内。然而,如果时间步长的数量不同,这将无法保持每一步的一致含义。
最好是不同时间步之间的关系最好保持一致,并且每个时间步的意义也应保持一致。另外,每个时间步还应有不同的表现形式。
这篇扩散模型的论文 使用了 Transformer 正弦位置编码 来保留时间步信息。Transformer 正弦位置编码是一种可以解决这些问题的方法,这种方法在注意力机制的论文 中提出。
参数在时间维度上是共享的,这是通过Transformer模型中的正弦位置嵌入来实现的。
位置编码(PE)的公式如下。
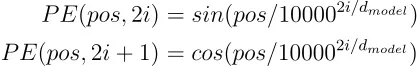
下面是一个用 Python 实现的例子,其中 pos 表示位置,i 表示维度。
class SinusoidalPositionalEmbedding(nn.Module):
def __init__(self, embedding_dim):
super().__init__()
self.embedding_dim = embedding_dim
def forward(self, timesteps):
positions = np.arange(timesteps)[:, np.newaxis] # 形状:(timesteps, 1)
dimensions = np.arange(self.embedding_dim)[
np.newaxis, :
] # 形状:(1, embedding_dim)
# 使用正弦函数来计算偶数索引的角度,使用余弦函数来计算奇数索引的角度
angle_rates = 1 / np.power(10000, (2 * (dimensions // 2)) / self.embedding_dim)
angle_rads = positions * angle_rates
# 创建一个与angle_rads相同形状的全零数组
pos_encoding = np.zeros_like(angle_rads)
pos_encoding[:, 0::2] = np.sin(angle_rads[:, 0::2])
pos_encoding[:, 1::2] = np.cos(angle_rads[:, 1::2])
return pos_encoding你可以试试通过运行这段代码来体验位置编码(PE)。
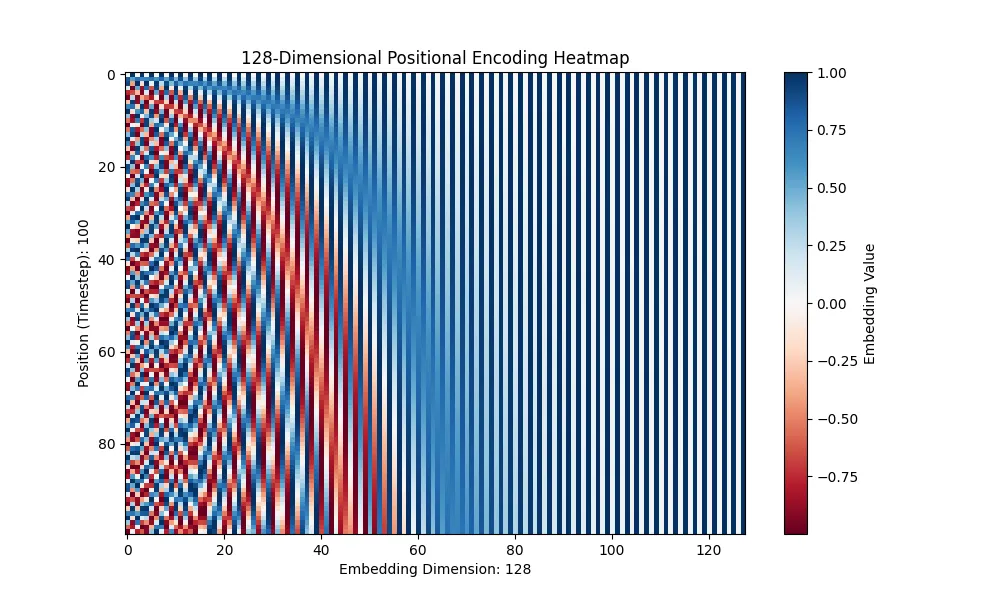
可以看出,通过使用_sin_和cos,可以在连续的时间点之间保持连续性。这使得模型可以轻松地学习到连续性。
此外,更重要的是,即使改变时间步长,也能保持信息的一致性,因此即使在推理时出现了一些训练时未提供的时间步长信息,模型也能很好地应对。
下面的 GIF 显示了时间步从 100 改为 500 时 PE 的情况。你可以看到位置信息保持一致。
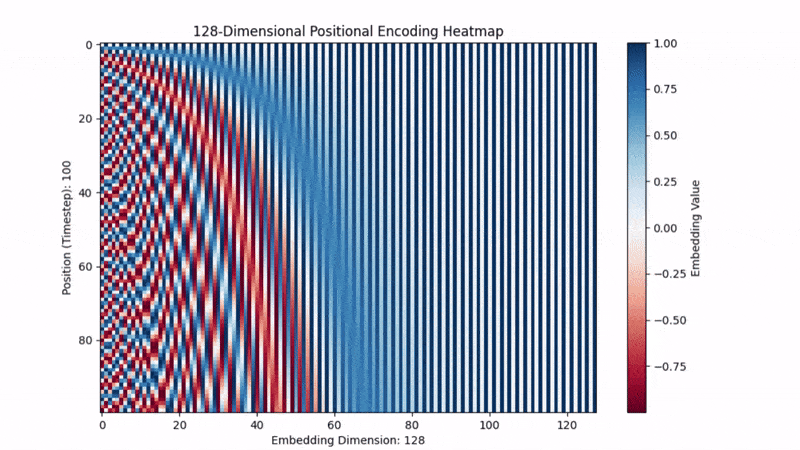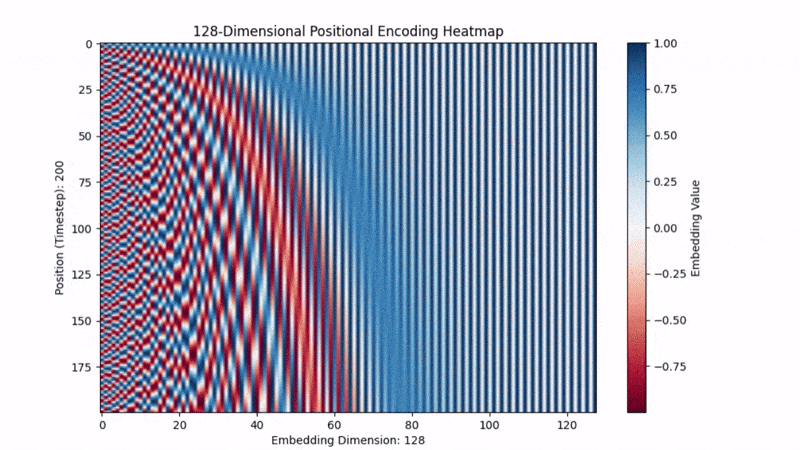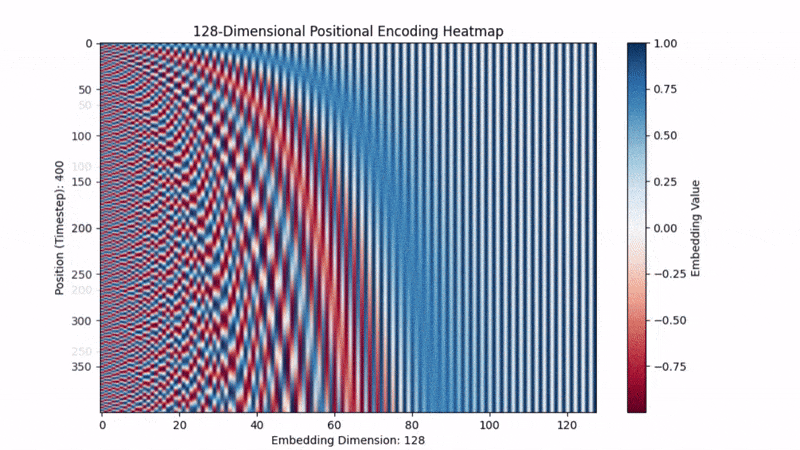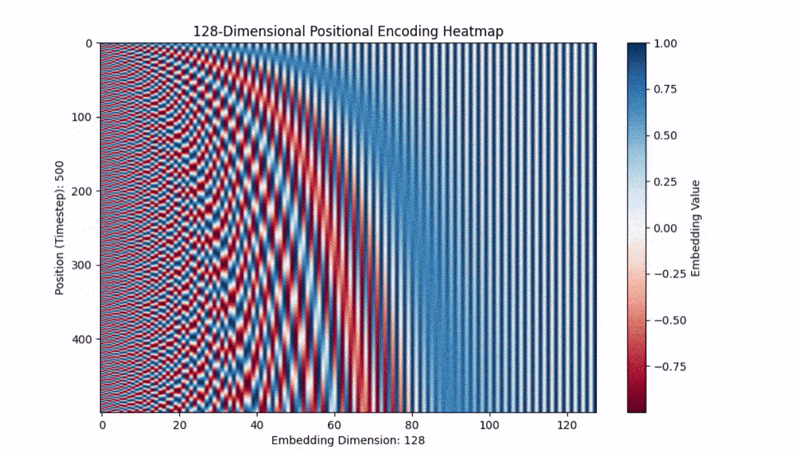
最后,PE在三角函数里为什么用数字10000?
论文中没有详细解释这一点,但也许10000只是一个合适的数值,虽然也可以选择其他数字。
下面这张图片是我将数值从10000改为了100以进行测试时拍下的。你看,波长变长了。
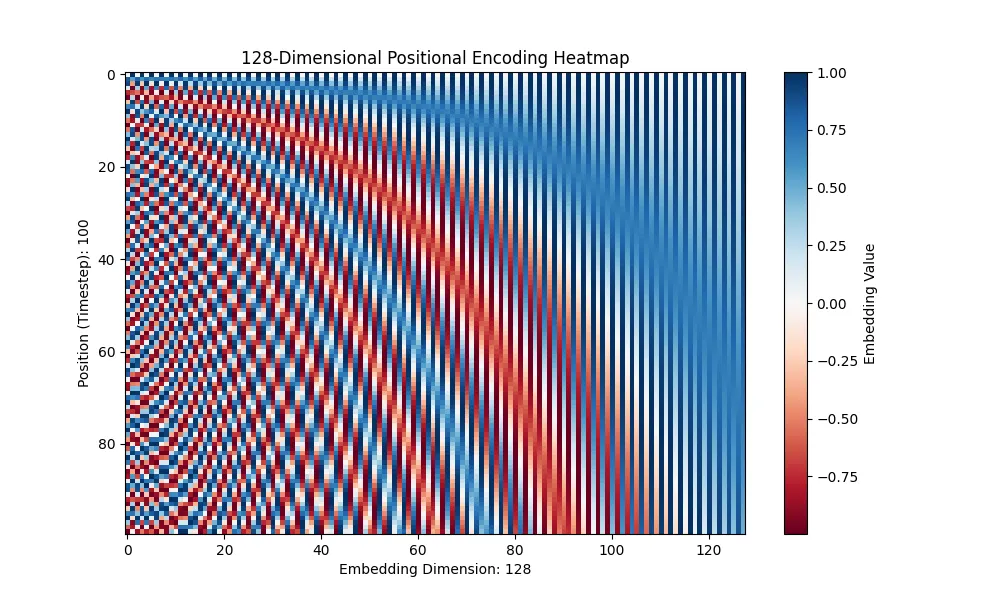

 随时随地看视频
随时随地看视频




