啊,矩阵。这是我们上学时遇到的线性代数的核心概念之一。尽管它们非常重要,但在我的职业生涯中,我从未有机会实际使用过它们,因此渐渐淡忘了它们的强大和灵活性。对我来说,这样的时刻出现在我开发Schemio的过程中,它是一款交互式图表编辑器。本文将探讨我如何利用矩阵解决一些棘手问题,适合所有对背后的数学原理感到好奇的人阅读。
Schemio 的早期日子当我刚开始构建 Schemio 的时候,一切都很简单:你可以创建形状,移动它们,调整它们的尺寸,甚至旋转它们。每个形状都是由位置(x, y)、大小(宽度,高度)和旋转角度定义的简单区域。简单得不能再简单了。表示图形的数据结构大致如下:
const diagram = {
name: "图表的名称",
// 所有对象都被表示为一个扁平数组
items: [{
id: "2563",
name: "Rect Yi",
shape: "rect",
area: {
// 位置(世界坐标)
x: 0, y: 0,
// 宽度 (w) 和高度 (h),单位均为像素
w: 100, h: 40,
// 旋转角度(度)
r: 0
}
}, {
id: "wer23",
name: "Ellipse Yi",
shape: "ellipse",
area: {
// 位置(世界坐标)
x: 100, y: 40,
// 宽度 (w) 和高度 (h),单位均为像素
w: 40, h: 40,
// 旋转角度(度)
r: 45
}
}]
};但当我想要添加一个项目层级时,事情变得有趣起来——允许用户将形状互相连接,并创建复杂交互。许多矢量图形编辑器支持分组功能,当移动一个对象时,组内的其他对象也会自动移动。但我想要更多。我设想了一个结合图表编辑器和游戏引擎的混合体,具有丰富的动画效果和自定义行为。因此,我引入了项目层级(通过在每个对象中添加“childItems”数组),满怀期待地开始了这项工作。
以下是在代码中最初项目结构的样子:
const item = {
id: "123",
name: "矩形 (Rectangle)",
shape: "rect",
area: {
x: 100, y: 400,
w: 80, h: 40,
r: 0,
},
childItems: [{
id: "462",
name: "椭圆 (Ellipse)",
shape: "ellipse",
area: {
x: 10, y: 0,
w: 30, h: 10,
r: 45,
},
childItems: [{
// 还有一个附加在椭圆的项目
}]
}]
};想象一下:你有一个矩形在图中。你将另一个形状附加到它上面,再把另一个形状附到它上面。现在旋转矩形,试试看会发生什么。如果你用SVG渲染,很简单——只需嵌套SVG元素,剩下的就由浏览器来处理了。但是Schemio不只是用来渲染的。你可能需要连接器连接对象,或者挂载和卸载对象,甚至执行一些自定义交互。对于这些操作,你需要能够在这两种坐标之间进行转换:局部坐标和世界坐标。
我的第一个方法很简单粗暴。我逐个检查了对象的父级链,并使用了一个简单的公式来应用变换操作。

后来,我通过缓存父变换来优化它,在一段时间内表现良好。但很快,我遇到了两个主要问题:缩放和支点。
缩放和枢轴点设置缩放功能使得能够动态调整对象的尺寸,而缩放中心点定义了旋转中心。能够应用缩放功能对Schemio而言是一个巨大的进步,使其能够动态加载外部图表。
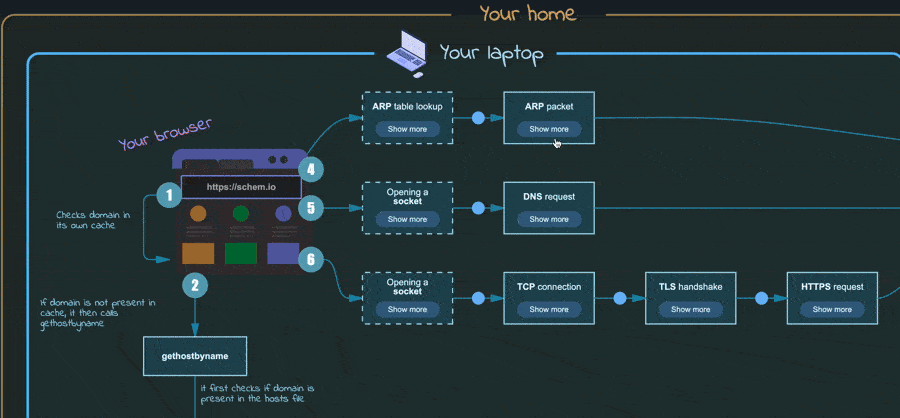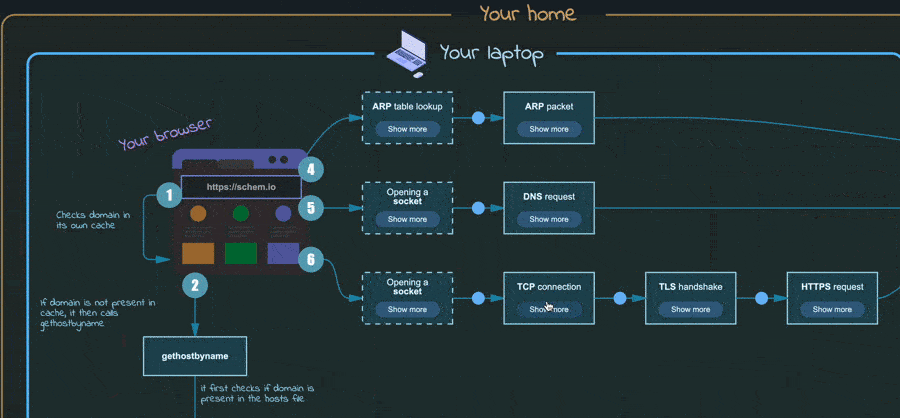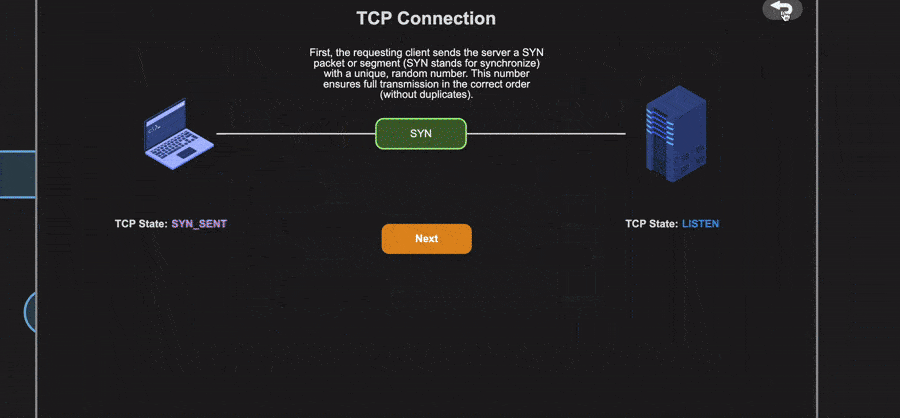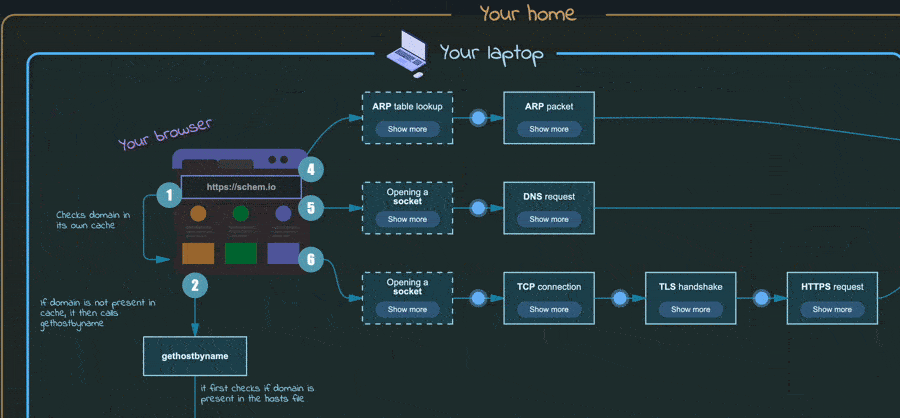
嵌套显示的外部图示演示
没多想我就给对象区加了4个额外的属性。更新后的区域结构如下:
const item = {
id: "123",
name: "矩形",
shape: "rect",
area: {
x: 100, h: 400,
w: 80, h: 40,
r: 0,
/*
px 和 py 表示相对于其宽度和高度的基准点,这样,当用户调整形状大小时,基准点也会随之调整
*/
px: 0.5, py: 0.5,
/*
sx 和 sy 是沿 x 和 y 轴的缩放因子
*/
sx: 1, sy: 1
},
childItems: [{
// 又一个附加到某个形状上的项目
}]
};但有了这些新要求,管理这些转换变得很混乱。这时我突然想到:矩阵来帮忙!
在二维(或三维)图形中,每一种转换——平移、旋转、缩放——都可以用矩阵来表示。例如,空间中的一个点可以表示为一个3×1的矩阵。要变换它,你只需将其与一个3×3的变换矩阵相乘。让我来给你讲解一些基本概念。
矩阵变换初学者指南我们从 单位矩阵(或称作身份矩阵) 开始,它表示没有任何变换。
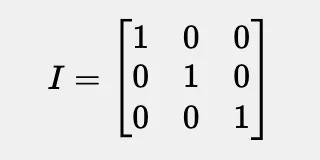
接下来是一个转换表:
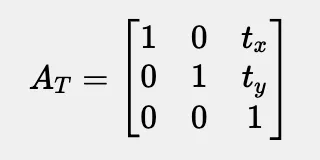
想旋转吗?用旋转矩阵。

调整大小时,可以使用缩放矩阵这一工具。

把这些结合起来就是神奇发生的地方。例如,要旋转并移动一个对象,将平移矩阵和旋转矩阵相乘。缩放和调整基准点也遵循类似的模式。
由于所有的变换矩阵都是3x3的,因此,二维点需要表示成一个3x1的矩阵。当你用一个3x3的变换矩阵去乘一个3x1的点矩阵时,得到的将是一个3x1的矩阵——这个3x1的矩阵就是变换后的点。基本上,所有的这些变换就是这样进行的!
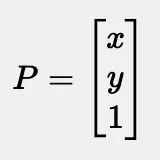
以下是对象的完整转换公式,

你可能要问的是,父对象变换矩阵是从哪里来的?其实它就是所有矩阵相乘的积。所以,如果我们遍历层次结构中的项目,可以用一个简单的公式来表示,例如:
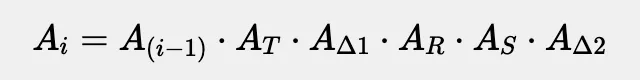
在上面的公式中,Ai 是当前对象的变换矩阵,而 A(i-1) 则是其父对象的变换矩阵。
我们来展开所有矩阵,并写出将局部坐标点转换为世界坐标点的完整公式。
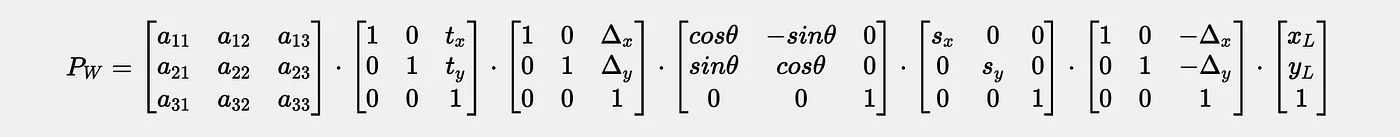
注意我们首先是将物体及其枢轴点一起进行转换,先应用旋转,再进行缩放,最后再将物体转换回来?这一点非常重要,以使物体看起来像是围绕选定的枢轴点旋转。
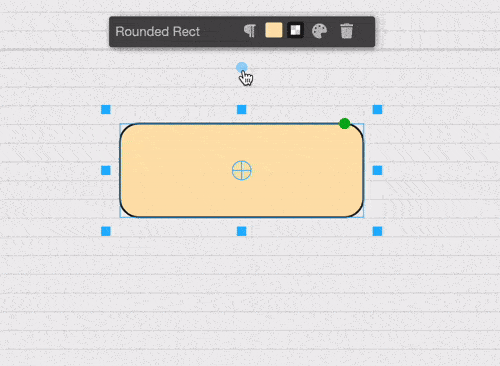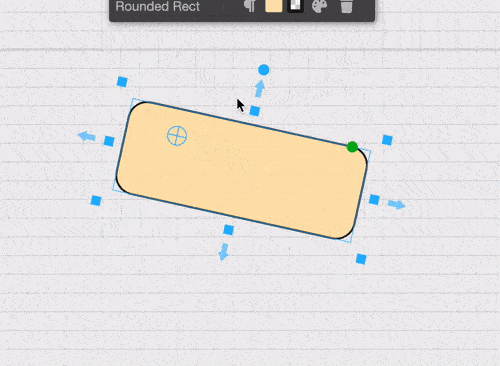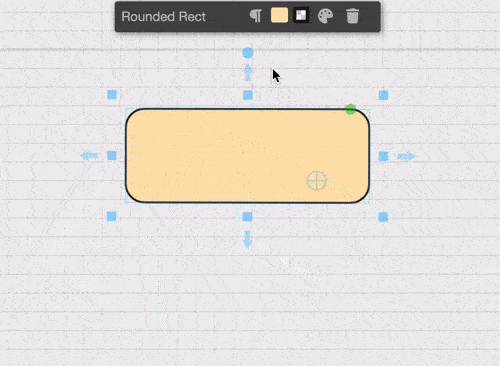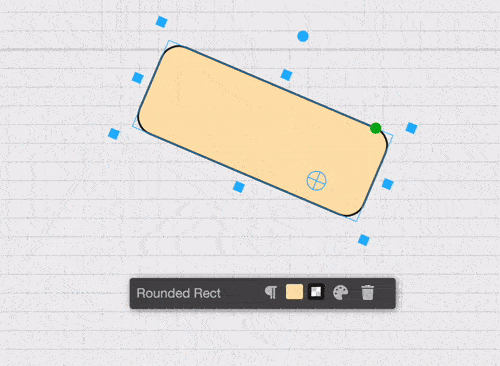
演示围绕中心点旋转的对象
如果我们没考虑枢轴点,旋转看起来就像是在左上角进行。这样就不理想,对吧?
另一个关键细节是,仿射变换公式中的基准点补偿发生在缩放矩阵后。这样可以确保当你缩放一个对象时,缩放看起来是以基准点为中心,使其在调整过程中保持不动。
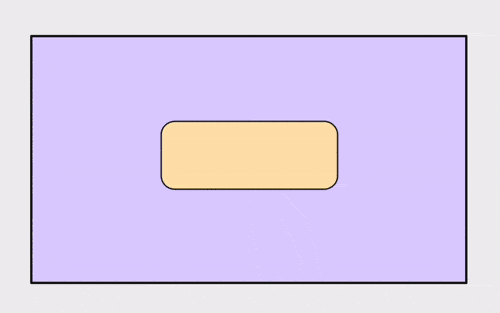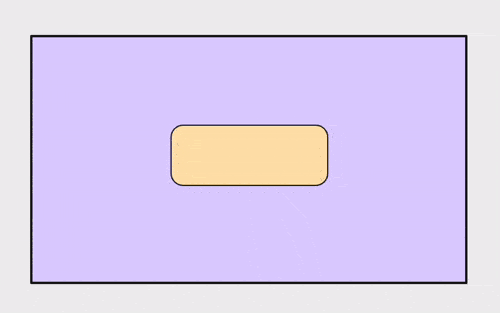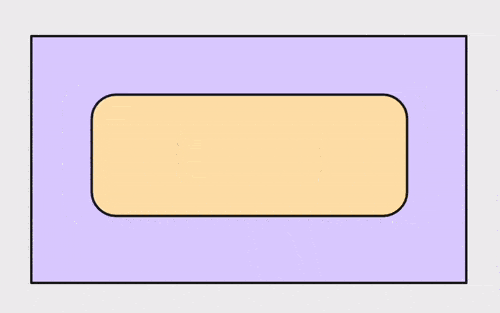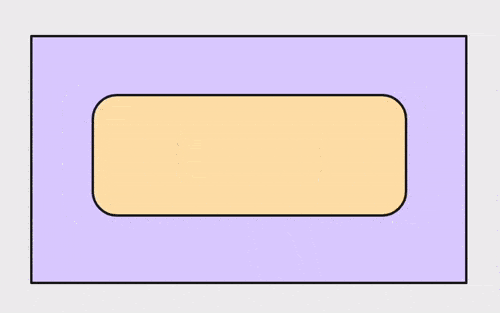
展示以中心为轴的缩放对象
世界坐标 vs 本地坐标你看,我们仅仅通过应用简单的矩阵乘法就已经取得了不少酷炫的结果。但这还不是真正的考验的结束。我在开发 Schemio 的过程中,棘手的地方不仅在于应用这些变换,而是如何在这两者之间进行坐标转换,反过来也一样。
这种映射对于连接器的连接或精确确定用户点击转换对象相对于其本地左上角的位置至关重要。我们已经知道了如何将本地坐标转换为世界坐标,现在让我们反过来解决相反的问题:将世界坐标点转换回对象的本地坐标。为此,我们将从本地到世界坐标的转换公式开始。
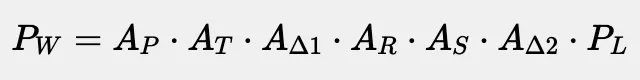
在上述公式中,除了本地点坐标以外的所有内容都已经知道了,因此,我们可以将矩阵简化并分组。
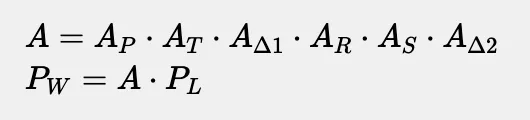
在这里,矩阵 A 表示一个对象的整个变换,包括它自身的变换以及所有父对象的变换。在线性代数中,矩阵不能直接相除,但有一个替代方法。你可以使用矩阵的逆。找到矩阵 A 的逆后,表示为 A⁻¹。
我不会详细讲解如何计算矩阵的逆,因为这在任何一本线性代数教材中都能找到,一旦我们得到了 A⁻¹,我们就可以从左边乘以等式的两边。
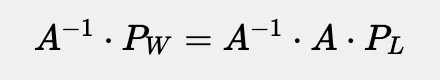
关于矩阵逆的一个很酷的地方是,一个矩阵和它的逆矩阵相乘会得到单位阵,这简化了一切。这意味着公式会简化为。
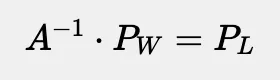
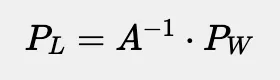
这便是!这便是将世界坐标转换为局部坐标的公式。矩阵使得这种转换更加有条理且更容易管理。没有它们,推导公式会变得更加复杂和混乱。
挂载与卸载对象:层级变换面临的挑战我在开发 Schemio 的项目层级特性时,遇到一个挺难的问题,那就是处理对象的 mounting 和 unmounting。这个问题有两种处理方式。
你可以把场景中的一个对象拖动到另一个对象的位置。
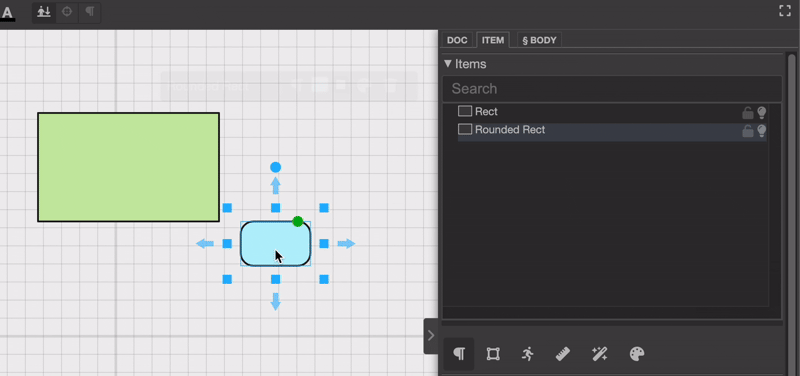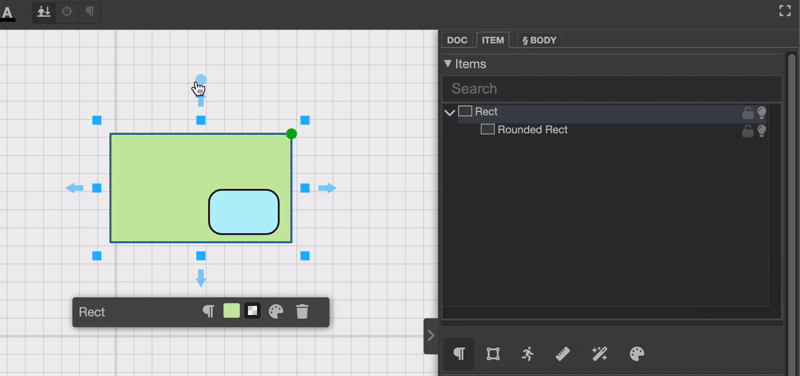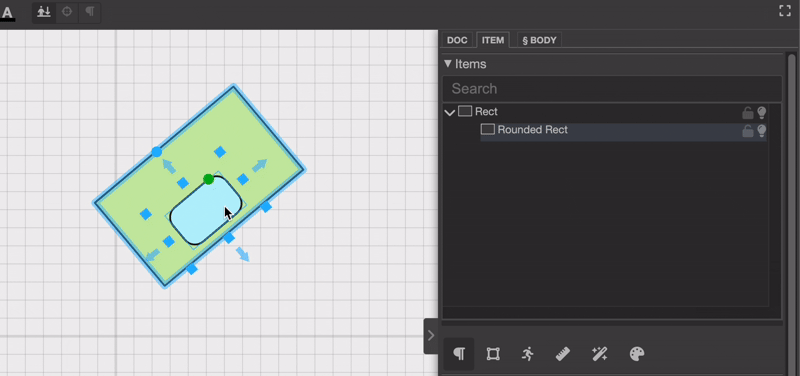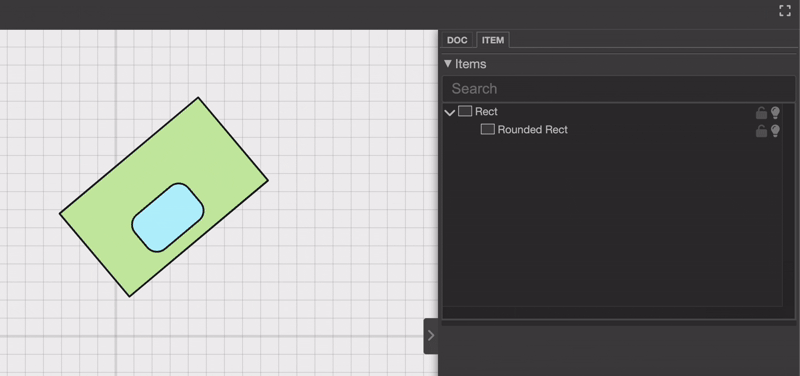
或者你也可以在项目选择器面板中调整层级。
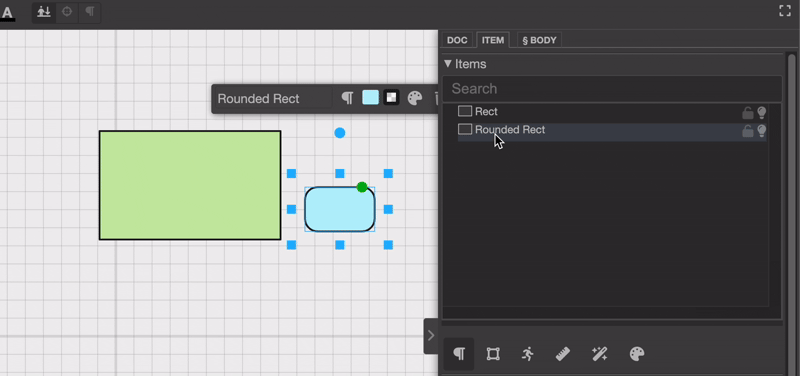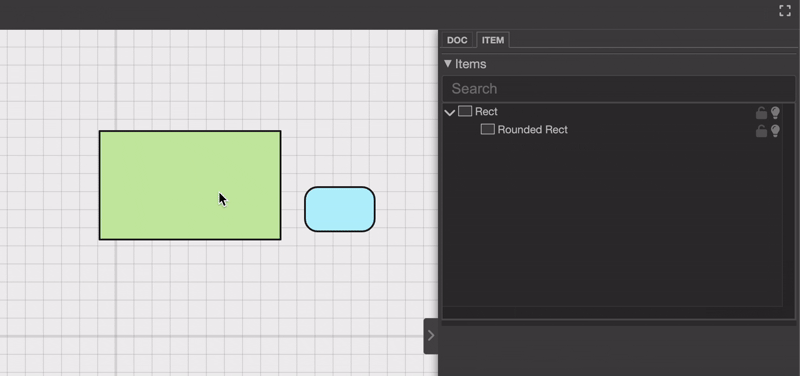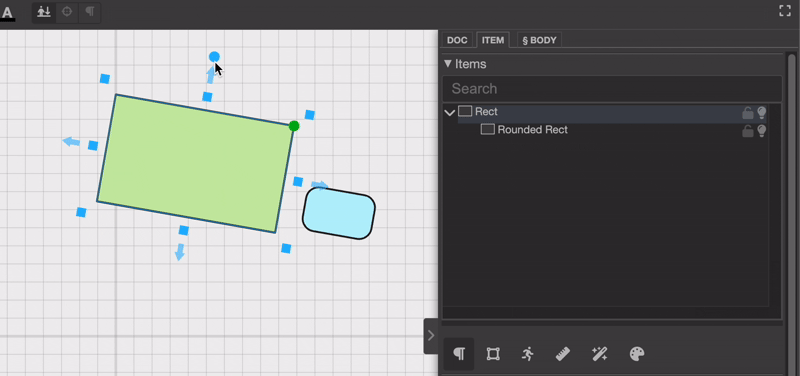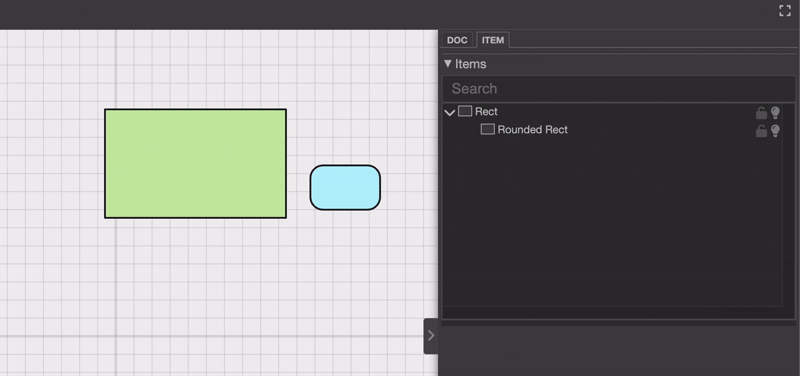
乍一看,这似乎并不复杂。只要更新项目的层级结构,就完成了,对吧?其实不然。真正的挑战在于重新计算被拖动对象的新位置和新旋转。这是为什么呢?因为每个对象的位置都是相对于其父对象定义的。如果你只是更改层级结构而不考虑这些变换差异,就会像这样:位置就会显得不正确。
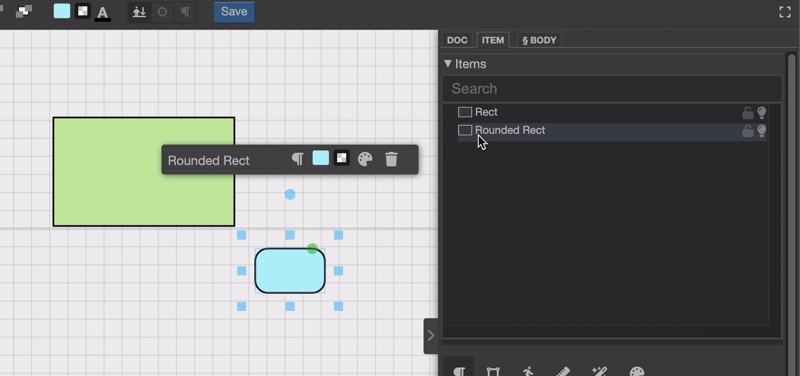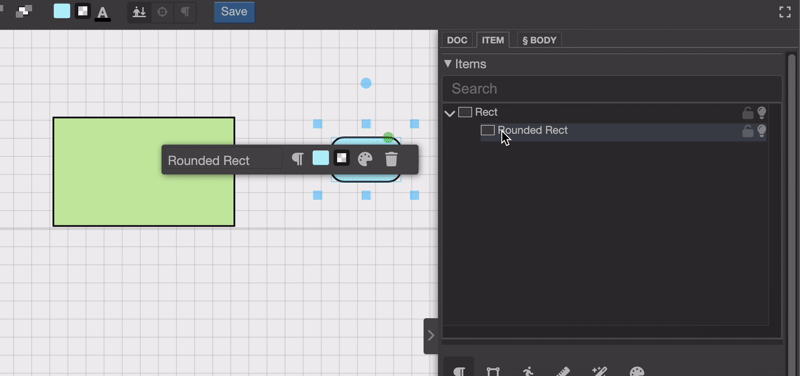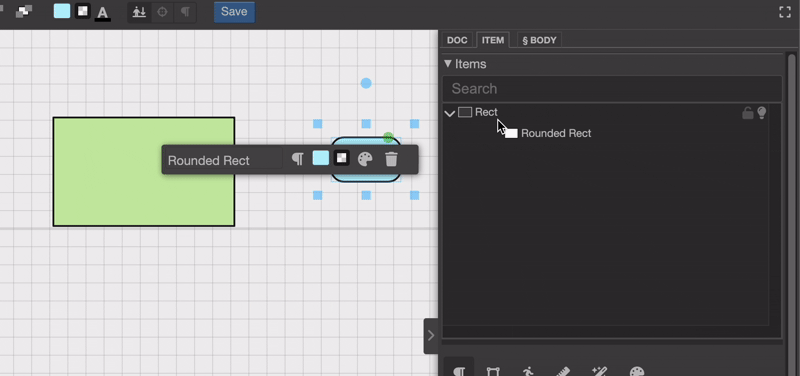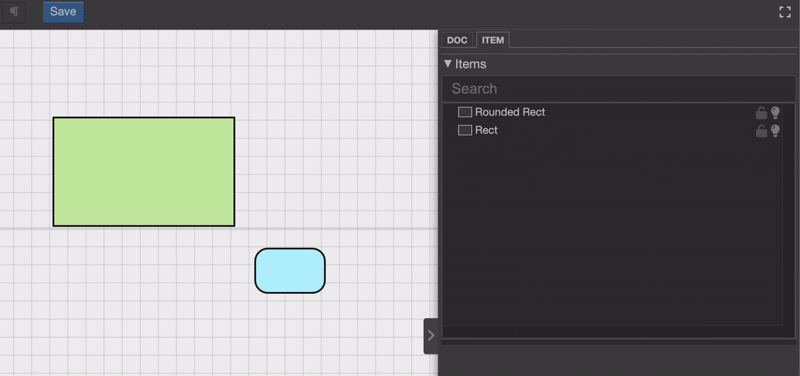
注意当将“圆角矩形对象”放到另一个对象上时,它会尴尬地上下跳动吗?这确实不太理想,对不对?那么,我们该怎么调整它的位置和旋转,让它不再跳来跳去呢?
步骤 1:记下拖动的对象的左上角的坐标我们将拖动对象的左上角在世界坐标系中的位置称为topLeftWorldPoint,这是在移动前需要获取的信息。
const 世界上的左上角点 = 项目上的世界坐标(0, 0, 项目);worldPointOnItem 这个函数实际上用了我们之前推导的那个矩阵公式。
接下来,我们需要调整拖动对象在不同父对象间移动时的旋转。想象你在将物品从一个父对象移动到另一个父对象。首先,计算当前父对象的全局旋转角度。由于一个对象的旋转是相对于其父对象定义的,我们使用名为 worldAngleOfItem 的函数将局部旋转转换为全局旋转。
function worldAngleOfItem(item, transformMatrix) {
// 计算左上角的世界坐标点
const p0 = worldPointOnItem(0, 0, item, transformMatrix);
// 计算右上角的世界坐标点
const p1 = worldPointOnItem(item.area.w, 0, item, transformMatrix);
// 从X轴到对象顶部边界向量的角度
return fullAngleForVector(p1.x - p0.x, p1.y - p0.y) * 180 / Math.PI;
}
function fullAngleForVector(x, y) {
const dSquared = x * x + y * y;
// 安全检查,归一化向量,将x和y分量除以向量的长度
if (!tooSmall(dSquared)) {
const d = Math.sqrt(dSquared);
return fullAngleForNormalizedVector(x/d, y/d);
}
return 0;
}
function fullAngleForNormalizedVector(x, y) {
if (y >= 0) {
return Math.acos(x);
} else {
// 否则
return -Math.acos(x);
}
}这个想法很简单:找到表示该项目本地X轴的向量,并将其映射到世界坐标系中。这个夹角就是世界旋转角度。然后对新的父对象重复同样的步骤,并相应地调整被拖动对象的旋转。
/* 将 previousParentWorldAngle 减去 newParentWorldAngle 后的结果累加到 item.区域.r 中 */
item.area.r += previousParentWorldAngle - newParentWorldAngle;现在,我们需要确保在移动到新父对象之后,被拖动的对象仍然保持在世界中的同一位置上。为此,我实现了一个名为 findTranslationMatchingWorldPoint 的函数,这个函数计算所需的平移,使指定的本地点与所需的世界点对齐。
const newLocalPoint = myMath.findLocalPointMatchingWorldPoint(
Wx, Wy, // 世界坐标点 x 和 y
Lx, Ly, // 物体上的局部点(x 和 y)
item.area, // 物体的区域对象
parentTransformMatrix // 父对象的转换矩阵
);
// 一旦我们得到了新的局部点,
// 我们只需要更新物体区域的 x 和 y 值。
// 这样,当我们拖动任何物体到其他物体上并改变其在项目层次结构中的位置时,
// 它将保持在屏幕上的相同位置
if (newLocalPoint) {
item.area.x = newLocalPoint.x;
item.area.y = newLocalPoint.y;
} 为了搞清楚这一点,让我们再来看看从局部点得到世界点的公式。
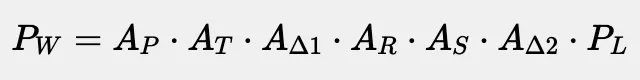
这儿:
- Pw(世界点)和 PL(局部点)已知,因为它们是函数参数,
- 唯一未知的是 At,即对象的变换矩阵。
把所有的已知矩阵合并成一个矩阵 A。
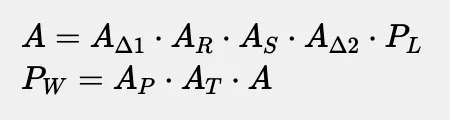
由于我们不需要调整对象的枢点或缩放比例,我们只需要新的 At 参数。为了更好地将其分离,我们再次运用矩阵求逆的技巧:
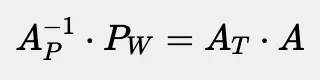
我们把父变换矩阵的逆改个名字,让它更清晰明了:
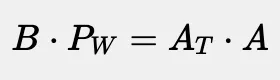
现在,这里有个难点——我们不能对矩阵A使用逆矩阵技巧,因为它是一个3x1的非方阵,只有方阵才能求逆。所以,我们来展开这个表达式:
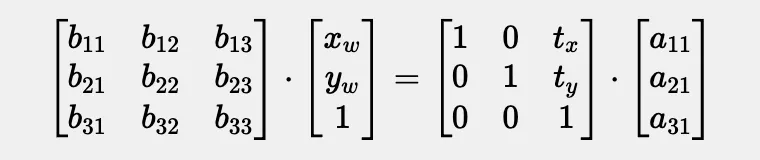
两边的矩阵相乘后,我们得到的就是这个。
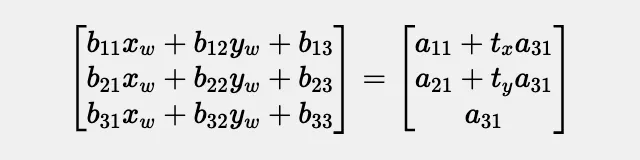
这样一来,我们就可以重点关注相关内容。
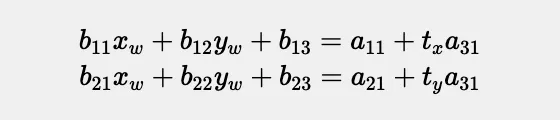
最后,我们终于得到了完整的那个公式:
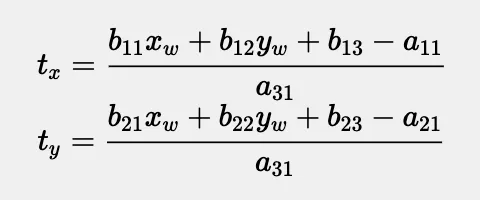
通过这些计算,被拖动的对象可以平滑地过渡到新的父对象,而不会有任何奇怪的跳跃或变形。这种方法不仅保持了对象的位置,还确保了它的旋转与新的层次结构完美匹配。
这真是一个很好的例子,展示了如何理解和应用数学概念——比如矩阵的逆和变换——如何让这样的复杂操作变得可能!
结尾我希望你喜欢这篇内容,并且对我在构建Schemio时遇到的数学挑战有所了解。如果你对这个项目感兴趣,想深入了解其实现细节,欢迎在GitHub上查看源代码:https://github.com/ishubin/schemio 。
想试试吗?访问https://schem.io,开始设计你自己的互动图或应用原型吧。
如果你对 Schemio 背后的更多数学挑战感到好奇,还有很多可以探索的!从贝塞尔曲线和微分学,到用于性能优化的四叉树结构,我很快会带来更多见解。敬请关注!

 随时随地看视频
随时随地看视频




