大家都知道,近年来扩散模型在各个领域产生了很大的影响。我想更了解这项技术,于是决定从零开始自己搭建它。
首先,我想了解一下训练损失,但是这比较复杂,而且论文中省略了一些细节,所以我试着自己研究和推导,并在这里总结了。基本上,它遵循论文去噪扩散概率模型中的方法。
首先,扩散模型有两个主要过程:正向过程和逆向过程。在正向过程中,噪声会逐步添加到输入数据里。在逆向过程中,通过执行正向过程的逆操作,从含噪声的数据中恢复原始图像。下面的图示能帮助你更直观地理解这些过程。
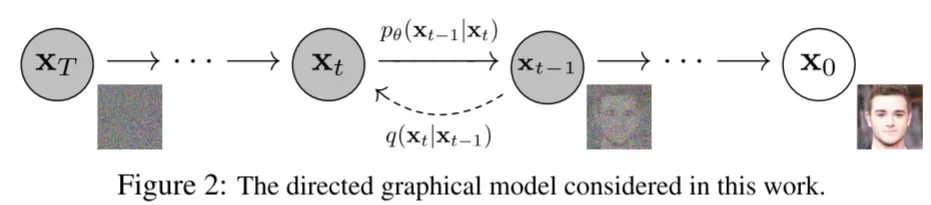
扩散模型是潜在变量模型的形式,形式如下 pθ (x 0):=∫ pθ (x 0:T )dx 1:T 。这种模型的联合分布 pθ (x 0:T ) 也称为反向过程,并定义为从 p(xT )=N(xT ;0,I) 出发的具有学得的高斯转移的马尔可夫链。
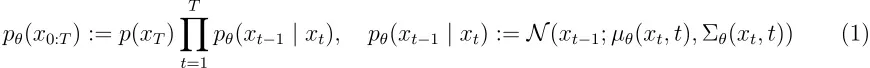
正向过程被设定为一个马尔可夫链,该链会根据方差计划 β 1, …, βT 逐渐向数据添加高斯噪声。
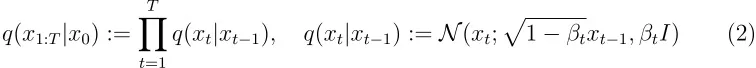
生成模型估计的数据概率如下。
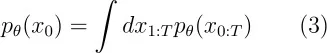
在原论文中,积分无法计算,所以公式变换如下,如下所示。
(Note: There seems to be a redundancy in the sentence "如下,如下所示". It should be revised to remove the repetition. The corrected version is as follows.)
在原论文中,积分无法计算,所以公式变换如下。
尽管论文中没有详细说明,但我个人觉得公式转换可能是通过正向过程完成的。这可能是由于正向过程有已知的概率分布,而反向过程的概率分布则可能更复杂,积分计算起来也更难。
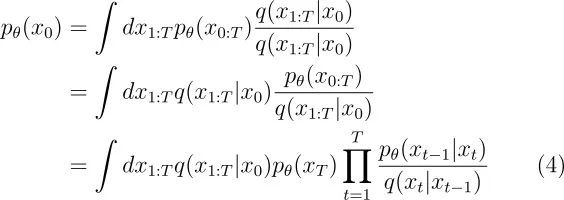
训练是通过优化负对数似然的变分界来进行的。下面方程通过詹森不等式得到一个上界,
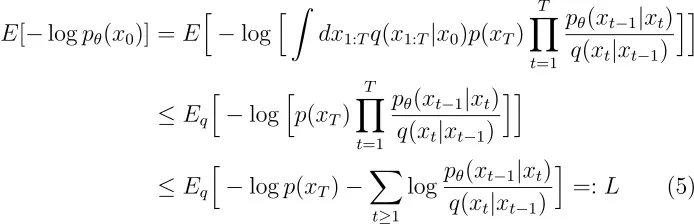
这个方程还可以这样进一步变换:
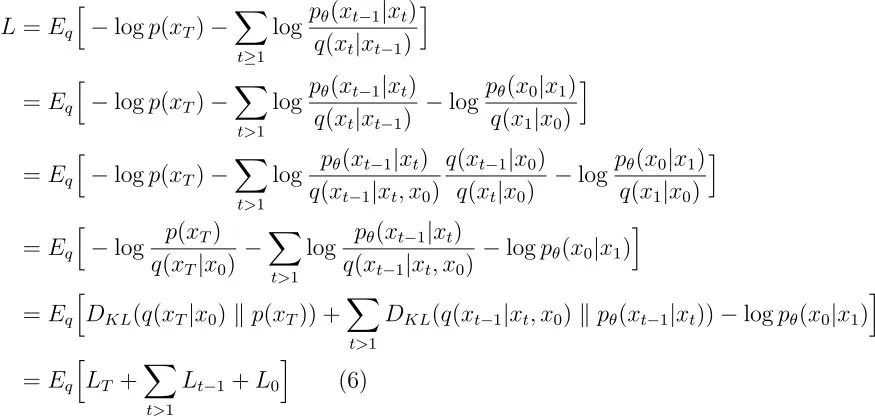
在上述方程的变形中,q(xt ∣ xt −1) 进行了如下所示的转换。
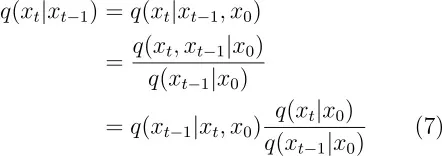
在上述方程式的转换过程中,使用了如下所示的关系。
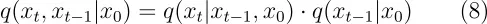
我也用了以下方程转换。
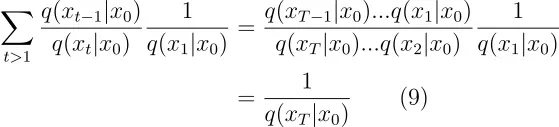
DKL 被称为 KL 散度,它是一种衡量概率分布 P 与另一个概率分布 Q 之间差异的统计度量。
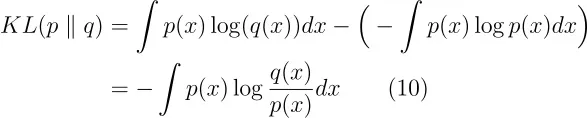
我们现在来简化方程(6)。
前向步骤和LT(请参见上下文以了解“LT”的含义)我们忽略了一个事实,即可以通过重新参数化来学习前向过程方差βt,而是将它们固定为常数。因此,在我们的实现中,近似后验_q_没有可学习的参数。因此,在训练过程中,_LT_是一个常数,可以忽略。
逆向和L1:T−1注:这里的"L1:T−1"是指特定的技术术语,可以理解为前一个时间点的状态。现在我们讨论在 pθ (xt −1∣ xt )=N(xt −1:μθ (xt ,t),Σ θ (xt ,t)) 中的选项,对于 1<t ≤ T 的情况。首先,我们将Σ θ (xt ,t) 设置为未训练的时间依赖常数 σt 2 I。实验表明,不论是 σt 2=βt 还是 σt 2=βt ~,结果都差不多。因此,我们可以将 Lt −1 写成如下形式。
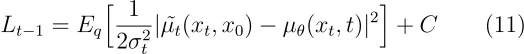
(C) 是一个不依赖于 (\theta) 的常数。因此,我们可以看出最直接的 (\mu_\theta) 参数化是将其直接设置为前向过程后验均值 (\mu_t) 的模型。我们可以使用以下方程来展开方程。这种变换被称为 重新参数化技巧。
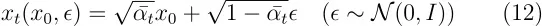
我们可以从上面的方程中得到 _x_0。

通过使用上述的 x 0,我们就可以更新 Lt -1。
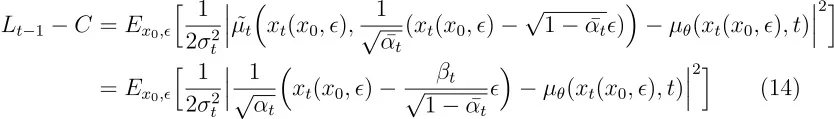
我们使用下面的 ( \bar{u_t}(x_t, x_0) ) 表示上述变换。附录 中解释了 ( \bar{u_t}(x_t, x_0) ) 和 ( \bar{\beta_t} ) 的推导。
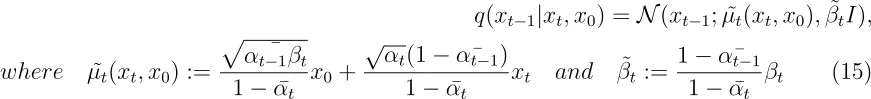
因为 xt 可以作为模型的输入,所以我们可以决定参数化。
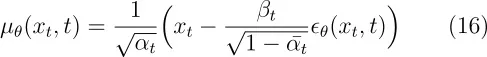
其中 ϵθ 是一个用来从 xt 预测 ϵ 的函数估计器。
我们可以用上面的方程来简化 (_Lt^{-1} - C)。
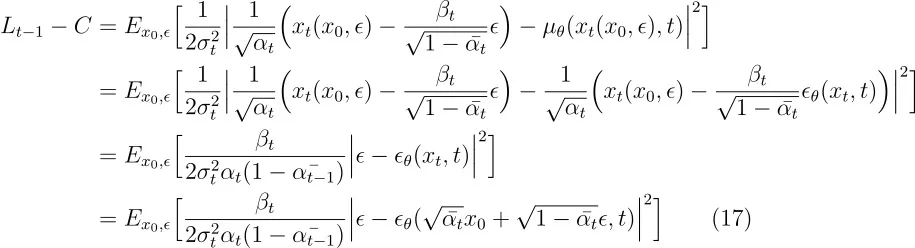
总之,我们可以训练逆过程的均值函数近似器 μθ 来预测 μt ~,或者通过调整其参数,我们可以训练它来预测 ϵ。
数据缩放(归一化),逆向过程解码器和L0我们假设图像数据由0到255的整数线性缩放至[-1,1]之间。这确保神经网络逆过程从标准正态先验p(x_T)开始处理一致缩放的输入数据。为了获得离散对数似然,我们将逆向过程中的最后一步设置为一个独立的离散解码器,该解码器源自高斯分布N(x_0;μ_θ(x_1,1),σ_1^2 I)。
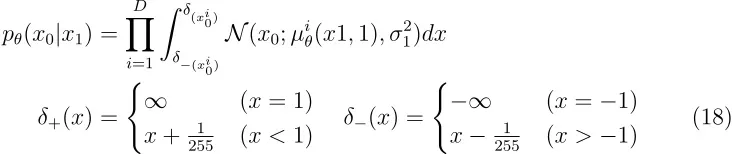
其中 D 是数据维度,而 i 上标表示提取一个坐标。上述方程计算了每个像素的同时概率。δ 表示裁剪界限,以此来将高斯概率密度限制在每个 _x_0i 的离散值对应的范围内。这样可以确保离散数据在连续框架中得到正确处理,以此确保在连续框架中正确处理离散数据。
简化后的训练目标
通过 Eq(17) 和 Eq(18),我们能更进一步地简化训练目标。
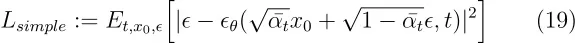
当 t=1 时,对应的是 L 0,其中离散解码器定义中的积分(公式(18))被近似为高斯概率密度函数乘以区间宽度的方式,忽略 _σ_12 和边缘效应的影响。当 t>1 时,这种情况对应的是公式(17)的未加权版本的形式。具体细节请参见文章,但使用这个简单的公式是因为移除公式(17)中的权重部分后,其准确性会更好。
附录:推导q(xt−1|x_t, x_0)的均值和方差条件分布 q(xt −1∣ xt ,x 0) 正比于以下两个分布的乘积。
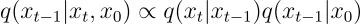
这两个分布的定义如下。
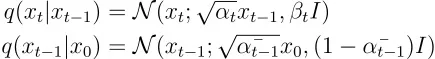
在计算方差时,我们利用高斯分布的乘积法则。在高斯分布的乘积形式下,方差的倒数表示为各个分布倒数的总和。

如果我们把两边交换以得到方差 βt ~
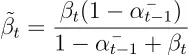
这里,我们使用以下属性。
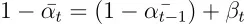
将其代入方差公式中,进行相应的转换。
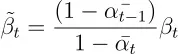
接下来,我们考虑均值的推导过程。设每个分布的均值分别为 m 1 和 m 2,方差分别为 σ 12 和 σ 22,均值可以按如下方式得出。
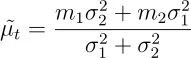
因此,我们可以通过以下方法计算平均数。
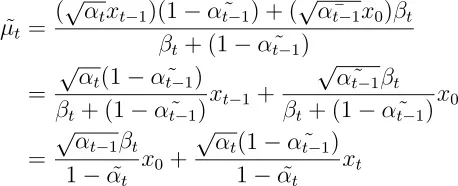
在这里面,我们又使用了下面这个属性。
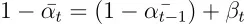
说实话,我真不确定这个推导是否正确。我也不知道为什么 xt −1 可以变成 xt 。这可能与我们首先用两个概率分布来近似 q(xt −1 ∣ xt , x 0) 有关。
参考文献:
 随时随地看视频
随时随地看视频




