RNN的输入数据是(time_stamps, input_features)
我们用这个数据集比如说
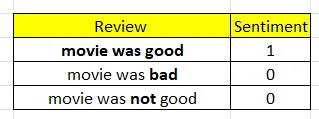
加粗的词就是我们要学习的词汇
我们的词汇表包括5个词:[电影、好、坏、不]。
所以目前,电影 可以被表示为 [1,0,0,0,0],是 可以被表示为 [0,1,0,0,0],好的 可以被表示为 [0,0,1,0,0],负面的 可以被表示为 [0,0,0,1,0],不 可以被表示为 [0,0,0,0,1]。
所以句子“这部电影不错”可以用向量形式表示如下:
[[1,0,0,0,0],[0,1,0,0,0],[0,0,1,0,0]]
所以我们一次一个词地将它们发送给RNN,这意味着在 时间戳 t=1 时发送词语“电影”,在 时间戳 t=2 时发送词语“是”,接着在 时间戳 t=3 时发送词语“好”。
所以,对于句子1(“电影不错”),输入数据的形状是(3,5),其中3表示时间戳,5表示特征总数。
对于第二句,输入数据的形状是(3,5),对于第三句,输入数据的形状是(4,5)
当我们使用keras 中的 SimpleRNN 类来编写代码时,我们将以此格式(batch_size, 时间步长, 输入特征)发送数据。假设我们一次发送所有三个句子,那么发送给RNN的数据将是(3, 4, 5),其中的4表示数据集中最长句子的时间步长。这就意味着这个三维张量将被输入到我们的RNN中。
RNN架构(循环神经网络架构)从现在开始,我们把第一个句子叫做X1,第二个句子叫做X2,第三个句子叫做X3。
X1的第一个词称为X11,第二个词称为X12,第三个词称为X13。同样的规则适用于X2和X3。
RNN与ANN非常接近。主要只有两个不同之处。
在 RNN 中,输入随时间传递,
在 t = 1 时,我们将 X11 发送给 RNN。
当 t = 2 时,我们将 X12 传给 RNN……等等
(注:根据建议,改为“当 t = 2 时”,“传给 RNN”,并简化省略号的使用,同时保留 RNN 英文原样。)
由于输出中不能包含注释,仅输出修改后的翻译:
当 t = 2 时,我们将 X12 传给 RNN,等等
ANN 是一种前馈神经网络,这意味着信息只从前向传递,即从输入端到输出端。
但是,RNN的结构就是这样

我们来画RNN架构
输入层要有5个神经元,每个词都将用一个由5个数字组成的向量来表示。
现在对于隐藏层来说,我们放3个神经元在里面
但因为这3个神经元是循环神经元,它们的输出会重新输入到自身。每个单元的输出也会传回同一层的其他单元。
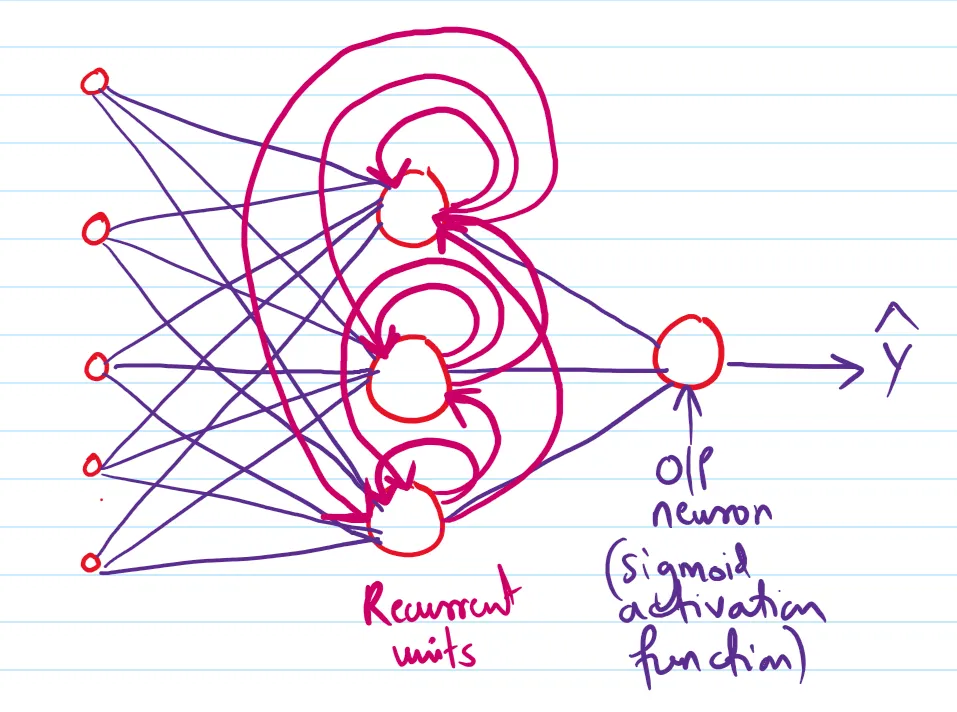
循环神经网络的架构实际上看起来像什么?
总共有这样的权重:这将涉及 53 个权重用于输入和循环层之间,33 用于循环层之间,还有 3 个用于循环层和输出之间,总计 27 个,即总共是 27。
总共有4个偏差,每个循环单元在隐藏层有3个偏差,输出节点有1个偏差。
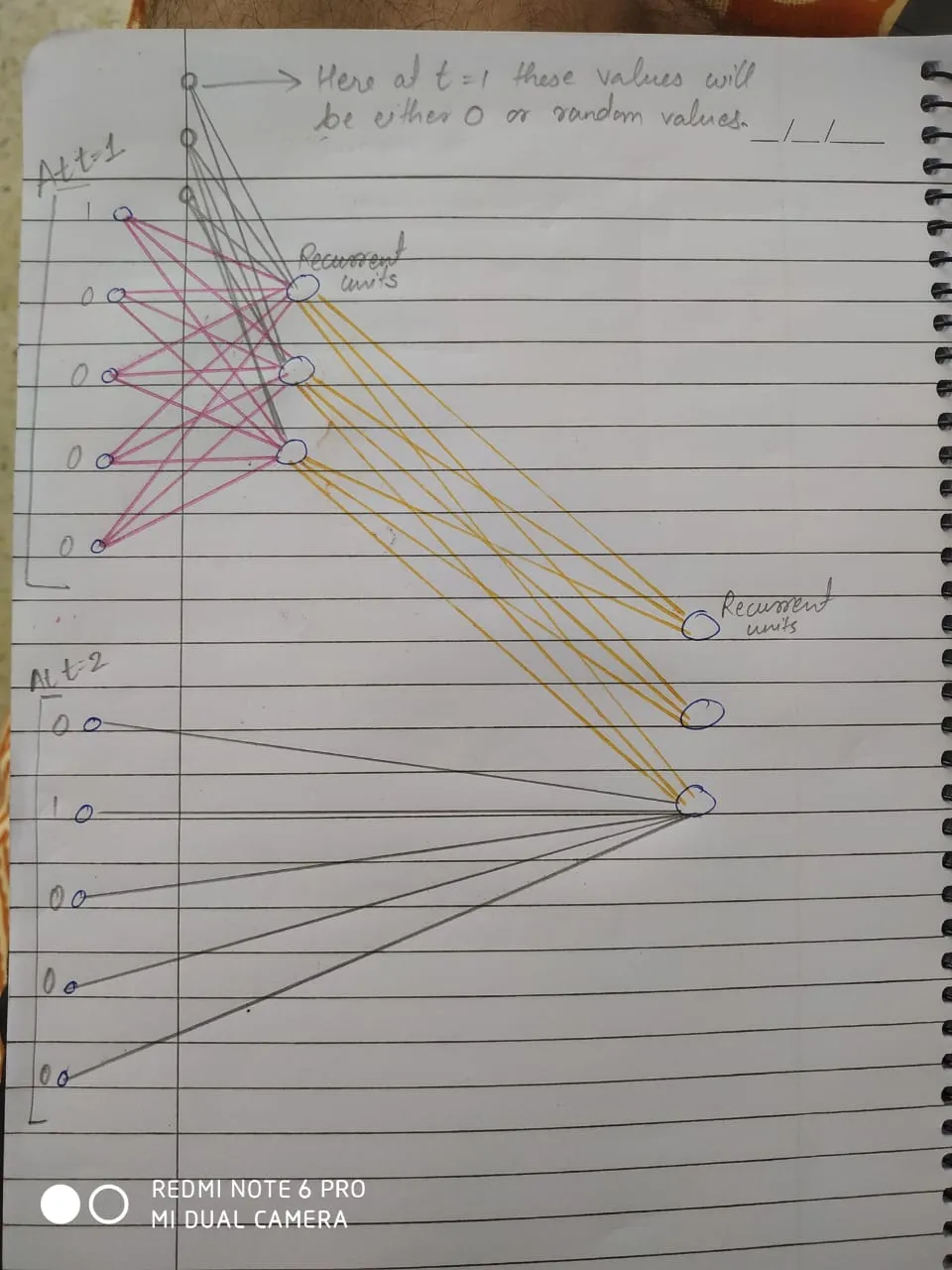
循环神经网络中的正向传播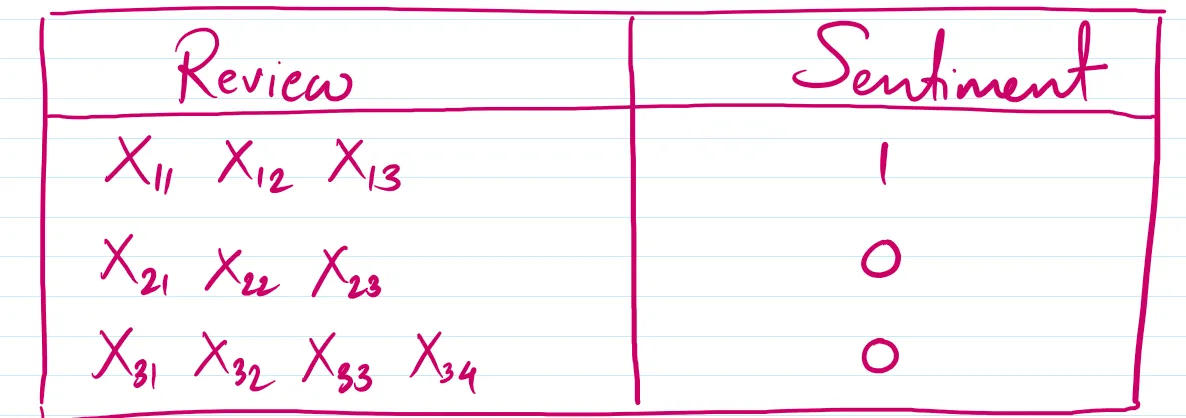
在我们的数据集中,X11 表示第一句话的第一个词,X12 表示第一句话的第二个词,X31 表示第三句话的第一个词。
注意 : X11 和 X12 都是向量,每个向量都是5维的(因为我们的语料库中有5个独特的单词,每个单词都会用这5个单词表示成一个5维的向量)
我们会一个接一个地把这些词传给我们的RNN(循环神经网络)。

我们的RNN模型
在进行正向传播时,我们遵循一个称为展开时间的概念,这其实就是递归层以循环方式工作。
循环层中的每个节点都具有激活函数,默认激活函数是 tanh

当 t 等于 1 时
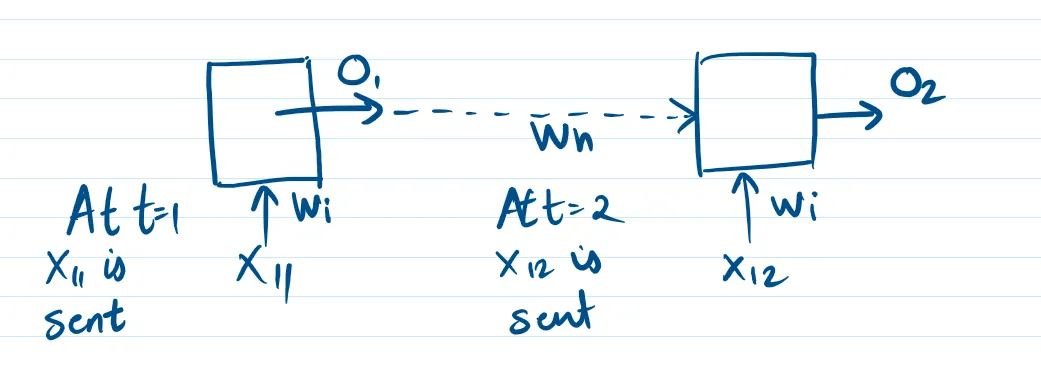
在 t 等于 2 的时候
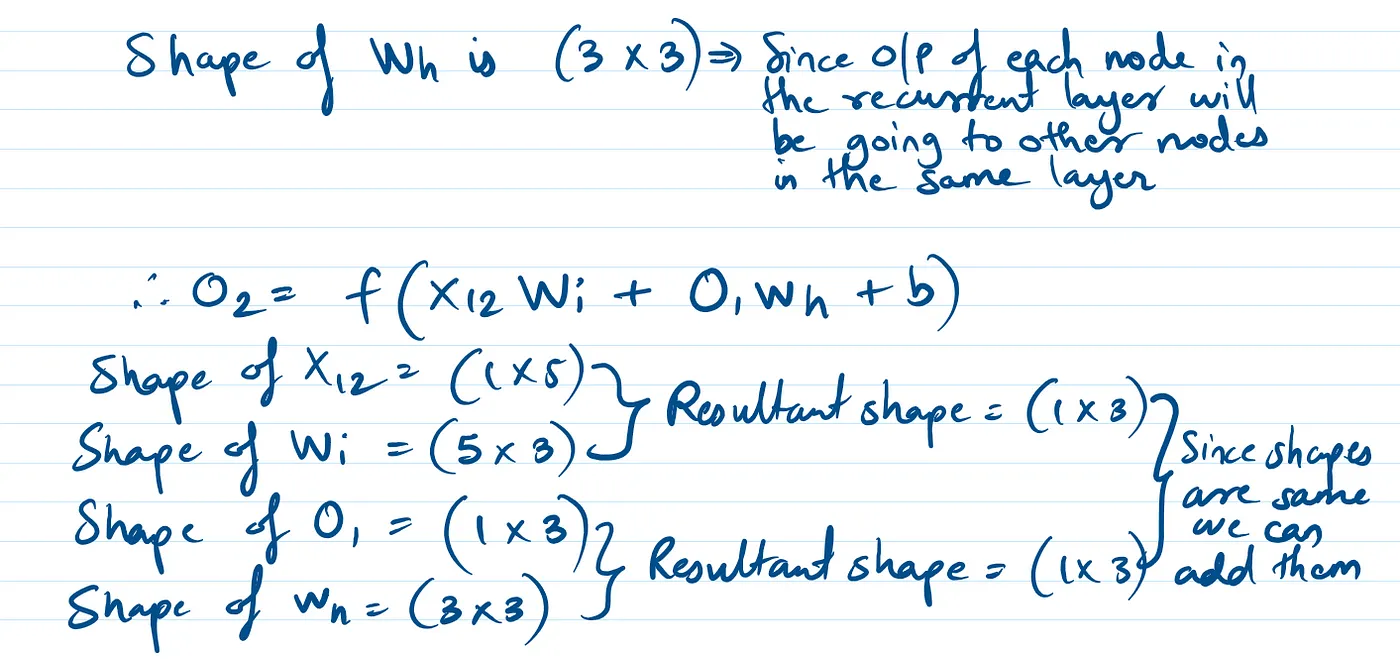
当 X12.Wi + O1.Wh + b 作为输入传给激活函数时,它会输出 O2。
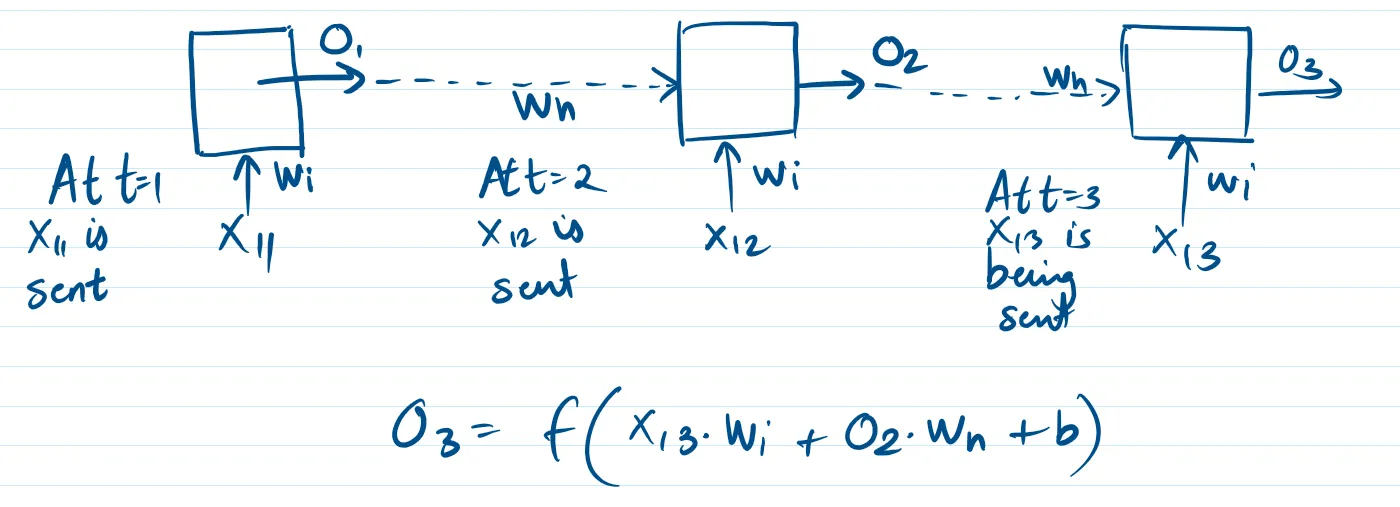
当 t=3 时
为了保持一致,在 t = 1 时刻,我们发送了 O0,它是一个 (1x3) 的向量,它要么包含所有 0,要么包含随机数。
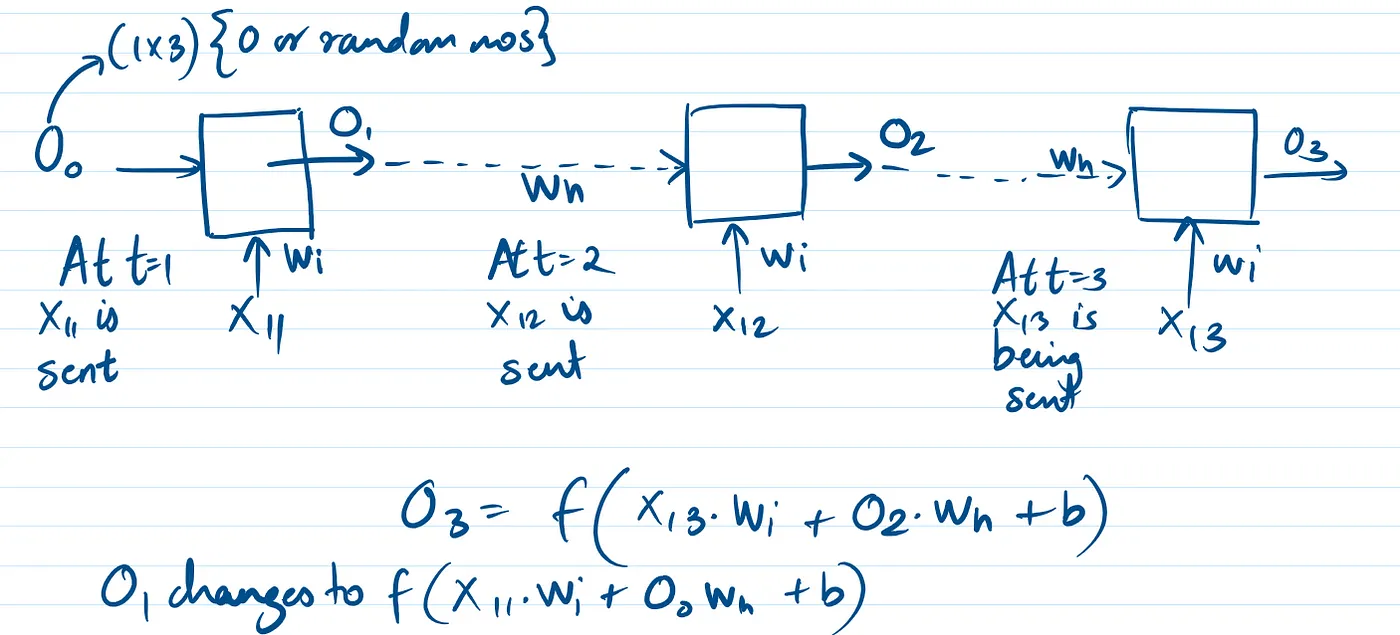
整体情况
为什么递归神经网络叫递归的?因为隐藏层在不断重复,或者说输入是一字一句地变化的,但我们每次都会用这一层来计算输出。
此外,每次给RNN模型新的输入时,但我们使用的是相同的权重,所以实际上我们是在利用参数共享(或权重共享)的概念。一个简单的RNN模型可以处理包含10个时间步的序列
RNN的简单表示方式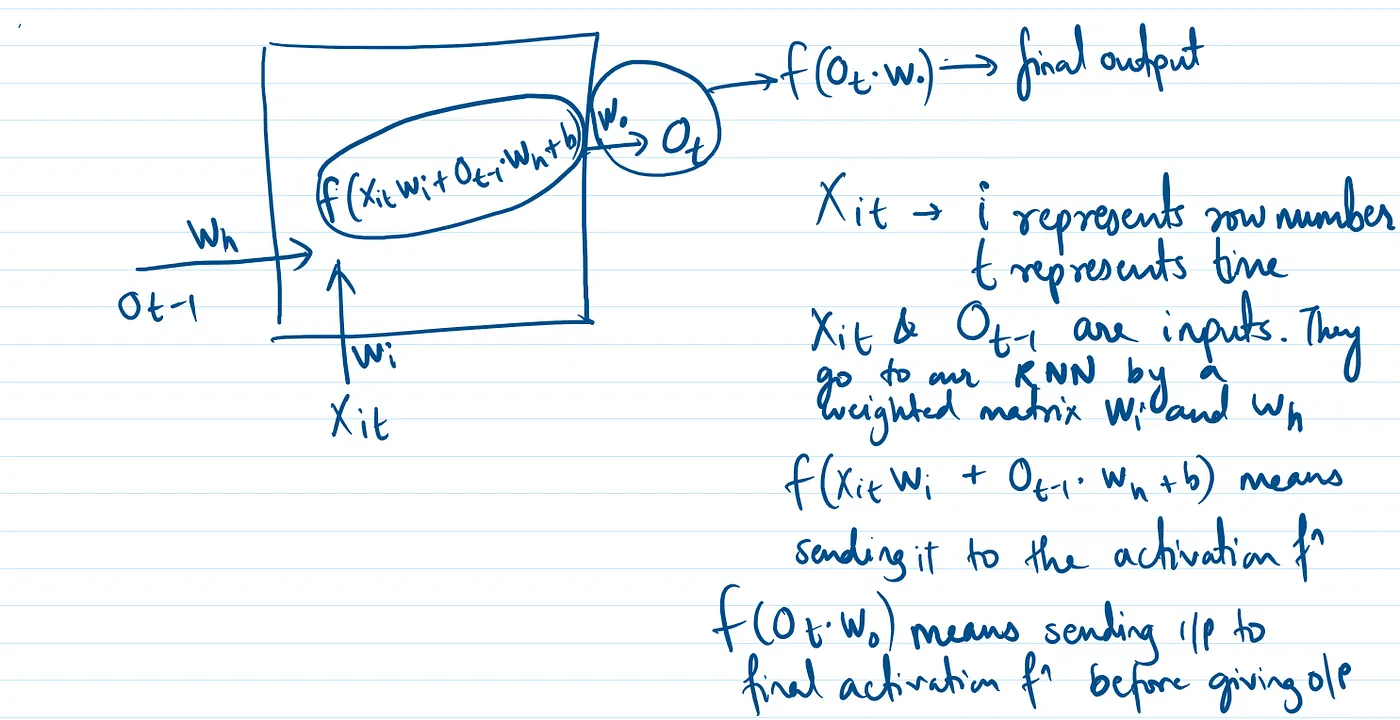

 随时随地看视频
随时随地看视频




