带有批归一化层的视觉变换器模型

将BatchNorm集成到标准的视觉变换器架构中是如何实现更快的收敛速度和更加稳定的网络性能的

比较有无批量归一化的视觉变换器在不同深度上的表现。

介绍

Vision Transformer（ViT）是首个纯粹基于自注意力机制的图像分类架构。虽然ViT表现得更好，但它们需要在非常大的数据集上进行预训练。为了寻找可以加快训练和推理速度的ViT的修改版本的尝试——尤其是在中等尺寸输入数据的情况下——我在之前的一篇文章中开始探索整合了批量归一化（BatchNorm）的ViT类型模型。批量归一化已知可以让深度神经网络更快地收敛——具有批量归一化的网络在相同训练周期内，准确率高于基线模型。这反过来也加快了训练速度。批量归一化还能有效地正则化网络，允许使用更高的学习率进行训练。本文的主要目的是探讨在Vision Transformer中引入批量归一化是否能带来类似的效果。

为了具体说明，我将专注于在ViT中的变压器编码器的前馈网络（FFN）中引入一个BatchNorm层，并省略FFN之前的LayerNorm层。在变压器的其他地方——包括自注意力模块——继续使用LayerNorm。我将称这种版本的ViT为ViTBNFFN——在前馈网络中具有BatchNorm的视觉变换器。我将在增强图像的MNIST数据集上训练和测试该模型，并与标准的ViT模型相比，在多个时期内比较该模型与标准ViT的Top-1准确率。我将为这两个模型选择相同的架构配置（即相同宽度、深度、补丁大小等），以有效地隔离BatchNorm层的影响。

这里是对主要发现点的简短总结:

1. 在选择合理的超参数（如学习率和批次大小）时，ViTBNFFN确实能比ViT更快地收敛，只要变压器的深度（即编码器的层数）足够大。
2. 随着学习率的提高，ViTBNFFN比ViT更加稳定，特别是在更深的网络层次中。

让我们从简要讨论深度神经网络中的BatchNorm开始，通过一个具体的例子来解释上面提到的一些特性。然后，我将详细讨论关于ViTBNFFN模型的架构。最后，我们将深入研究BatchNorm对视觉Transformer的影响。

数据集：含图像增强的MNIST

我们先来介绍将在本文中用于所有数值实验的增强版MNIST数据集。训练和测试数据集可以通过函数_get_datasets_mnist()_获得，如下面的代码块1所示。

代码块 1. 通过对 MNIST 数据集进行增强获得的训练数据集和验证数据集。

重要的代码位于第5到第10行，列出了我将使用的一些图像增强的细节。我引入了三种不同的变换方法，如下所示。

1. RandomRotation (degrees=20) : 图像随机 旋转，旋转角度在 (-20, 20) 范围内。
2. RandomAffine (degrees = 0, translate = (0.2, 0.2)) : 随机 仿射变换，具体来说，其中 translate = (a, b) 表示水平和垂直偏移量分别在 [- image_width × a, image_width × a] 和 [-image_height × b, image_height × b] 区间内随机采样。degrees=0 表示不旋转，因为我们已经通过随机旋转考虑了这一点。这里也可以加上缩放变换，但我们使用缩放操作来实现这一功能。
3. RandomZoomOut (0, (2.0, 3.0), p=0.2) : 随机 缩放变换，在区间 (2.0, 3.0) 内随机选择一个浮点数 r，并输出宽度为 input_width × r 和高度为 input_height × r 的图像。浮点数 p 表示执行缩放操作的概率。这个变换后跟着一个 Resize 变换，来确保最终图像的大小被调整回 28 × 28。

深层神经网络：批归一化

让我们简单回顾一下BatchNorm是如何提升深度神经网络性能的。假设( zᵃᵢ )表示给定层的输入数据在深度神经网络中，其中( a )是批次索引，从1到( Nₛ )，( i )表示特征索引，从1到( C )。BatchNorm操作则涉及以下一些关键步骤：

对于给定的特征索引 i，我们首先计算一批数据（即大小为 Nₛ 的）的均值和方差（即平均值和方差）。

2. 用上述计算出的均值和方差（其中 ϵ 是一个很小的正数）来对输入进行标准化：

3. 最后一步，对于每个特征 i，将其标准化输入变换和缩放:

在这种情况或表达中没有求和操作，这些参数 (γᵢ, βᵢ) 可以被训练。

我们来看一个用于分类MNIST数据集的深度神经网络。我将选择一个由3个全连接隐藏层组成的网络，每个隐藏层有100个激活单元，并且每个隐藏层都使用了Sigmoid激活函数。最后一个隐藏层连接到一个具有10个输出的分类层，对应于MNIST数据集的10个类别。输入到该神经网络的是一个形状为b × 28²的二维张量——其中b是批量大小，每个28 × 28的MNIST图像被展平成一个长度为28²的向量。也就是说，每个图像的特征索引从1到28²。

此模型与最初的BatchNorm 论文 中讨论的模型类似，我称这个模型为 DNN_d3。可以考虑在每个隐藏层的 sigmoid激活函数前 添加一个BatchNorm层的版本。让我们将生成的模型称为 DNNBN_d3。想法 是看看引入BatchNorm层后网络性能会怎样变化，以理解BatchNorm层的引入如何影响网络性能。

接下来，我们要使用上述描述的MNIST数据集来训练和测试这两个模型，使用CrossEntropyLoss()作为损失函数和Adam作为优化器，训练轮次为15个。对于学习率为lr=0.01和训练批次大小为100（测试批次大小设定为5000），模型的测试准确度和训练损失如图1所示。

图1. 两个模型（如下）在学习率0.01时，15个周期内的准确率测试结果（左）和训练损失结果（右）。

显然，引入BatchNorm使得网络更快地收敛——DNNBN（深度神经网络批量归一化，DNNBN）达到了更高的测试准确率和更低的训练损失。因此，BatchNorm可以加快训练过程。

如果增加学习率会发生什么？一般来说，较高的学习率这可能会导致梯度爆炸现象或梯度消失现象，从而使训练变得不稳定。特别是，较大的学习率从而在反向传播过程中产生更大的梯度。然而，BatchNorm 确保了通过一层的反向传播不受该层参数缩放变换的影响（更多细节请参阅这篇论文的第 3.3 节 this paper）。这使得网络更能抵抗由于高学习率引起的不稳定性。

为了明确地展示这一点，让我们以学习率 lr=0.1 来训练这些模型。在这种情况下，模型的测试准确度和训练损失如图2所示。

图2. 两个模型在15个迭代、学习率0.1时的准确率（左）和损失（右）。

高学习率明显地让DNN变得不稳定。然而，带有BatchNorm的模型却表现得非常好！更直观地展示这种行为的方法是将两个学习率对应的准确率曲线绘制在同一张图中，如图3所示。

如图3所示，DNN_d3（左）和DNNBN_d3（右）在两个不同学习速率下的准确率曲线。

当DNN_d3模型在高学习率下停止训练时，DNNBN_d3的性能影响则温和得多。因此，BatchNorm允许在更高学习率下训练模型，提供了另一种加快训练速度的方法。

ViTBNFFN 模型：在前馈网络中的批量归一化

让我们先简要回顾一下标准视觉Transformer在图像分类任务中的架构，如图4所示。更多细节，请参阅我之前写的文章文章或在Towards Data Science 上发表的关于该主题的众多优秀综述之一。

图4所示，ViT架构的示意图表示。

从架构角度来看，视觉变换器可以大致分为三个主要组件如下：

1. 嵌入层： 这一层将图像映射成一个“句子”——即一系列标记，每个标记都是维度为 dₑ（嵌入维度）的向量。给定大小为 h × w 且有 c 个颜色通道的图像之后，首先将其分割成 p × p 大小的补丁并展平，这将得到 (h × w)/p² 个展平的补丁（或标记），每个标记的维度是 dₚ = p² × c，然后通过一个可训练的线性变换将其映射成维度为 dₑ 的向量。在标记序列末尾添加一个可训练的标记——即 CLS 标记，用于分类任务。示意如图所示：

最后，向这个令牌序列加入一个形状相同的可学习张量，这个张量用来编码位置嵌入信息。这个序列随后被送入变压器编码器。这样编码器的输入就变成了一个形状为 b × N × dₑ 的3D张量，其中 b 表示批次大小，N 表示包括CLS令牌的令牌数量，dₑ 则是嵌入维度。

2. Transformer编码器: Transformer编码器将一个令牌序列映射到另一个具有相同数量和相同形状的令牌序列。换句话说，形状为b × N × dₑ的输入3d张量被映射到相同形状的另一个3d张量。编码器可以有L个不同的层（定义为变压器的深度），每个层由两个子模块组成，如图5所示——多头自注意力（MHSA）和前馈网络（FFN）。

图5. 编码器中的Transformer子模块。

MHSA模块实现了从形状为b × N × dₑ的3d张量到相同形状的3d张量的映射，该映射将转换为相同形状的3d张量，然后被输入到FFN中，如图2所示。这是不同令牌的信息通过自注意力映射混合的地方。MHSA模块的配置通过固定头部数量nₕ和头部维度dₕ来决定。

FFN是一种深度神经网络，包含两个线性层和一个中间的GELU激活层，如图6所示。

图6. 位于transformer编码器一层内的FFN模块（前馈神经网络模块）。

此子模块的输入是一个形状为 b × N × dₑ 的三维张量。左侧的线性层将其转换为形状为 b × N × d_mlp 的张量，其中 d_mlp 是网络的隐藏维度大小。经过非线性 GELU 激活后，第二个层将该张量映射回原始形状。

3. MLP 头： MLP 头是一个全连接的网络，将变压器编码器的输出——形状为 b × N × dₑ 的 3d 张量——映射成 b × d_num 的二维张量，其中 d_num 表示图像分类任务中的类别数量。这是通过首先从输入张量中提取出 CLS 令牌，然后将其输入到全连接网络中来完成的。

该模型ViTBNFFN除以下两点不同外，其他部分与上述架构相同。首先，在编码器的前馈神经网络（FFN）中，于第一个线性层和GELU激活之间插入了一个批归一化层，如图7所示。其次，删除了标准ViT编码器中FFN之前的层归一化层，如上图5所示。

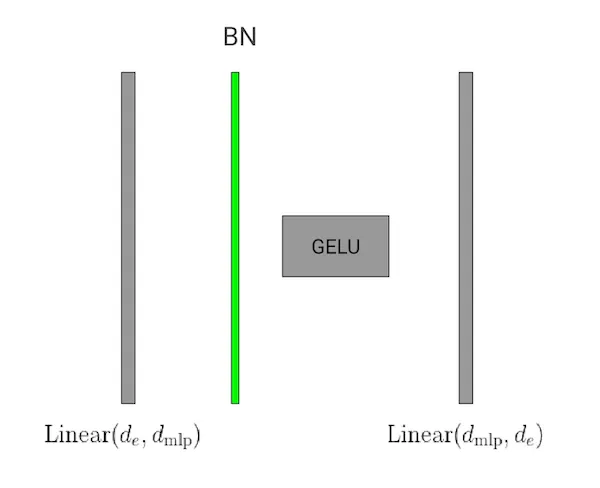
这是用于ViTBNFFN模型的FFN子模块（图7）。

因为线性变换作用在输入张量（形状为 b × N × dₑ）的第三维度上，所以 dₑ 实际上就是批归一化中的特征维度。新的前馈网络的 PyTorch 实现请参见代码块 2。

代码块 2：用于 ViTBNFFN 的 FFN 模块，其中包含批归一化（BatchNorm）。

内置的 PyTorch BatchNorm 类总是将张量的第一个索引作为批量索引，将第二个索引作为特征索引。因此，在应用 BatchNorm 之前，需要将我们的 3d 张量从形状 b × N × dₑ 转换为形状 b × dₑ × N 的张量，并在之后再转换回形状 b × N × dₑ。此外，我使用了 2d 的 BatchNorm 类（因为它比 1d 的 BatchNorm 稍微快一些）。这需要将 3d 张量提升到形状为 b × dₑ × N × 1 的 4d 张量（第 16 行），然后转换回（第 18 行）形状为 b × N × dₑ 的 3d 张量。可以使用 1d 的 BatchNorm 类，而不影响该部分展示的结果。

实验室里的实验

使用固定的学习率和批量大小，我将首先在增强的MNIST数据集上训练和测试这两个模型——ViT和ViTBNFFN，共进行10轮，并比较在验证集上的Top-1准确度。因为我们对研究批量归一化的影响感兴趣，所以需要将这两个模型以相同的配置进行比较。实验会在变换器编码器的不同深度下重复进行，其他配置保持不变。我在本次实验中使用的这两个模型的具体配置如下：

1. 嵌入层：MNIST 图像是一个 28×28 的灰度图像。补丁大小为 7，这意味着，除了 CLS 标签外，还有 16 个标记，总共 17 个。嵌入维度 dₑ 为 64。
2. Transformer 编码器：MHSA 子模块具有 nₕ = 8 个头，每个头的维度为 dₕ = 64。FFN 的隐藏维度 d_mlp 为 128。编码器的深度是架构中唯一可变的参数。
3. MLP 头仅包含一个线性层。

训练和测试批次大小将分别固定为100和5000，所有时期都将使用(CrossEntropyLoss())作为损失函数和(Adam)优化器。嵌入层和编码器中的 dropout 参数均被设置为零。我使用了型号为NVIDIA L4 Tensor Core GPU的设备，并可从Google Colab获取，通过MLFlow的跟踪功能记录了所有运行。

我们先用 lr=0.003 的学习率训练和测试模型。下面的图8总结了四张图，这些图分别展示了深度为 d=4、5、6 和 7 的两个模型的精度曲线。在这些图中，符号 ViT_dn (ViTBNFFN_dn) 表示深度为 n 的 ViT (ViTBNFFN)，其余配置与上述相同。

图8. 在lr=0.003时，对于深度分别为4、5、6和7的两个模型的精度曲线进行比较。

对于 d=4（左上）和 d=5（右上），两个模型的准确率相当——在 d=4 时，ViT 稍微胜出一点，而在 d=5 时，ViTBNFFN 轻微超越了 ViT。当 d<4 时，准确率仍然相当。然而，对于 d=6 和 d=7（下行图），ViTBNFFN 的表现明显优于 ViT。可以验证，当深度 d≥6 时，这种现象会保持一致。

让我们将学习率 lr 设置为 0.005，再次进行实验。图 9 总结了深度分别为 d=1, 2, 3 和 4 的两个模型的准确率曲线。

图9. 当lr设置为0.005时，两个模型在不同深度下的精度曲线的对比，深度分别为1、2、3和4。

对于 d=1 和 d=2（位于顶部的两个图表），两个模型的准确度相当——对于 d=1，ViT 的表现稍好一些，而对于 d=2，它们几乎看不出区别。对于 d=3（左下角的图），ViTBNFFN 的准确率略高于 ViT。然而，对于 d=4（右下角的图），ViTBNFFN 的表现明显优于 ViT，这种特征在任何更深的 d ≥ 4 的情况下都保持一致。

在我考虑的超参数范围内，对于合理选择的学习率和批量大小，ViTBNFFN 在变压器编码器达到一个关键深度之后，比 ViT 收敛得快得多。这个关键深度似乎随着固定批量大小下的学习率增加而减小。

对于深度神经网络的例子，我们看到使用批归一化（BatchNorm）的网络中，高学习率的影响相对较小。对于视觉变换器（Vision Transformer），是否也有类似的现象发生？这在图10中有所展示。每个图分别展示了在特定深度下，使用 lr=0.003 和 lr=0.005 两种学习率的模型的准确率曲线。第一列图对应于 ViT，深度分别为 d=2、3 和 4（自上而下），而第二列图则对应于同样深度的带有批归一化和前馈网络的 ViT (ViTBNFFN)。

图10展示了在不同深度下，两种不同学习率下的ViT（Vision Transformer）和ViTBNFFN（Vision Transformer with BNFFN）的准确率曲线图。

考虑 (d=2) — 由图的最上面一行给出 — 随着学习率的增加，ViT 和 ViTBNFFN 的影响程度相当。对于 (d=3) — 由图的第二行给出 — 差异显著。在较高的学习率下，ViT 的准确率显著下降，从约 91% 下降到第 10 个 epoch 结束时的约 78%。相比之下，对于 ViTBNFFN，第 10 个 epoch 结束时的准确率仅从约 92% 轻微下降到约 90%。这种定性特征在更深的网络中仍然保持不变 — 请参见底部一行的图，对应 (d=4)。因此，对于足够深的 transformer 编码器，较高的学习率对 ViTBNFFN 的影响显得温和得多。

结论部分。

在这篇文章中，我研究了在Vision Transformer的变压器编码器中的前向网络内部引入BatchNorm层的效果。通过在增强版的MNIST数据集上比较模型，可以得出两个主要结论。首先，对于足够深度的变压器以及合理选择的超参数，带BatchNorm的模型相比标准ViT模型具有显著更高的准确性，这可以大大加快训练过程。其次，类似于我们对深度神经网络的直觉，带有BatchNorm的Vision Transformer更能承受更高的学习率，这一点值得注意，前提是编码器足够深。

感谢阅读！如果您读完了这篇文章并且还喜欢它，请留下点赞和/或评论，并请关注我，获取更多精彩内容。未特别说明，本文中的所有图片和图表均由作者制作。谢谢！