大约几周前,有一个问题出现在《悉尼晨锋报好周末问答》栏目中。详见这里:https://www.instagram.com/goodweekendquiz/p/DAt26iSPKeE
马姆齐酒是什么?是轻微的宿醉、女巫的诅咒,还是加强型葡萄酒?
假设我们对这个问题完全不了解,有没有办法在这种情况下做出一些有根据的猜测呢?我认为可以。
不妨先想一想,再往下读也没问题。

使用 Gemini Imagen 3 创建的,一个有些宿醉的巫婆,她喝了烈酒。
我们真的对此无能为力吗?看着这个单词,它似乎可以是这些选项里的任何一个。这种多项选择题当然就是要让人觉得难以抉择,对吧?
但这里有一个理性的处理方式,那就是承认每个选项都具有不同的“基础率”。也就是说,暂时忘记什么是马尔维扎酒,什么是不是马尔维扎酒,我们可以感觉到,可能不像巫术咒语有那么多名字,宿醉的名称相对较少,而各种加强型葡萄酒的名称则肯定更多,种类繁多。
进一步量化这一点
- 多少词用来形容轻微的宿醉?大概一个吧?
- 咒语的词有多少?虽然我不是专家,但已经能想到一些同义词,所以大概有十个吧?
- 烈酒的词有多少?虽然我不是专家,但我能说出几个(波特酒、雪利酒)而且可能还有更多的,所以大概有一百个吧?
因此,没有其他线索判断哪个可能是正确的答案,蒸馏酒会是一个合理的猜测。根据我上面的大致估计,蒸馏酒比轻微的宿醉更有可能是正确答案,可能性高100倍;比诅咒的可能性高10倍。
即使我对这些数量的估计不太准确,但我至少对这个概率有信心,所以我会把加强酒视为我的最佳猜测。
哇哦!Bingo(宾果!一家马德拉葡萄酒与美食的网站)
基准率忽视这种推理可能看似简单,但在做此类判断时忽视基础率是我们常见的偏误之一,这被卡内曼和特沃斯基等人广泛讨论过。一旦我们意识到这一点,就会发现这种偏见随处可见。
请看罗尔夫·多贝勒的《The Art of Thinking Clearly》中的以下脑筋急转弯:
马克是一个来自德国的瘦男人,戴着眼镜,喜欢听莫扎特。马克更可能的是(A)卡车司机还是(B)法兰克福的文学教授?
根据我们对描述形成的刻板印象,可能会倾向于选 B,但更合理的猜测可能是 A,因为德国的卡车司机比法兰克福的文学教授多得多。
这个谜题借鉴了卡尼曼和特韦尔斯基的图书管理员和农民的角色设定(见判断与不确定性),这也为3B1B关于贝叶斯定理的伟大解说提供了框架(参见这段视频),在这个解说中,这种思维方式被映射到了贝叶斯公式中的条件概率和先验概率。
发现思维陷阱贝叶斯框架帮助我们更清楚地识别概率推理中常见的两种陷阱。按照 Kahneman 和 Tversky 的说法,我们可以说它为系统二(慢思考)提供了一个工具来纠正我们冲动且容易出错的系统一(快思考)。
首先,我们发现,给定 B 事件发生时 A 事件的概率 p(A|B) 并不等于 A 事件发生时 B 事件的概率 p(B|A),但在日常生活中,我们常常会错误地认为这两个概率是相同的。
在多贝利的例子里面,这个不同点是:
- P(👓|🧑🏫) — 在马克是法兰克福的一位文学教授来说,马克是一位来自德国、戴眼镜、喜欢听莫扎特的男子的概率
- P(🧑🏫|👓) — 在马克是来自德国、戴眼镜、喜欢听莫扎特来说,马克是一位在法兰克福的文学教授的概率
如果相信固定思维,上面的 P(👓|🧑🏫) 似乎相当可能,而 p(🧑🏫|👓) 则不太可能,因为我们认为在德国有很多人符合同样的描述,但并不是文学领域的教授。
第二个洞察是,这两个条件概率相互关联,因此知道其中一个就能得出另一个。要连接这两个条件,我们需要A和B各自的独立概率,而比例因子实际上是这两个独立概率的简单比率,如下所示:
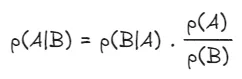
这张图片是作者做的
这就是贝叶斯法则。
贝叶斯推理 — 一步一步来那这怎么帮我们呢?
除了教科书和示例玩具模型之外,我们不会期望能够拥有所有可用于贝叶斯公式计算的数字,但它仍然为我们整理已知和未知并形成合理的猜测提供了一个有用的框架。
比如,对于多贝利的情境,我们可以从以下估算开始。
- 戴眼镜且符合特定描述的教授的比例:25%(每4人中有1人)
- 在德国法兰克福担任文学教授的比例:0.0002%(每500,000人中有1人)
- 戴眼镜且符合特定描述的卡车司机的比例:0.2%(每500人中有1人)
- 在德国从事卡车驾驶的比例:0.1%(每1,000人中有1人)
- 符合特定描述的一般人群中戴眼镜的比例:0.2%(每500人中有1人)
- 德国人口:8500万
这些参数都是我个人根据自己的世界观进行的估计。只有德国的人口是我可以查到的数据。这会帮助我更理性地思考多贝利提到的问题。
下一步是将这些数据放入交叉表中,这些表格展示了每种事件单独发生以及同时发生的相对频率。从总体人口开始,利用我们的百分比估算,我们可以开始为法兰克福的教授和卡车司机分别制作两个表格,以符合描述的要求(对于这一部分,您可以参照这个电子表格:this spreadsheet)。
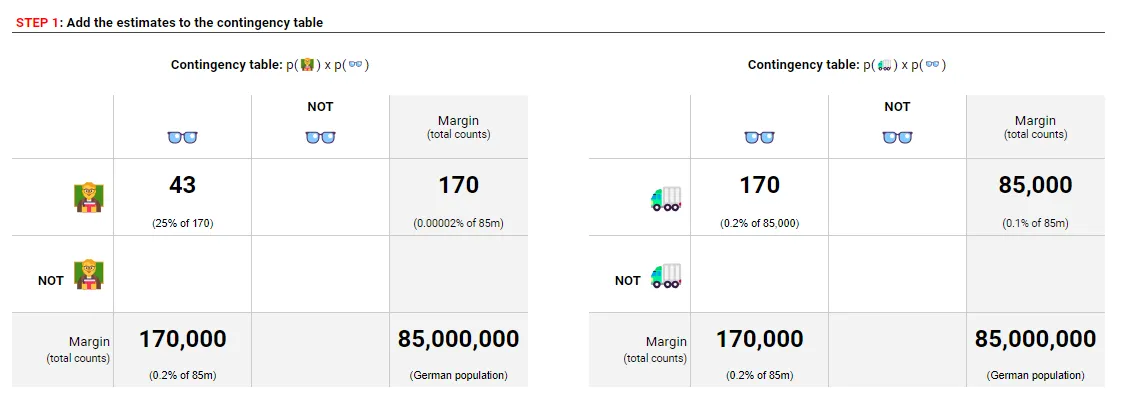
图片和资源由作者制作,查看此处以查看原始文档
这四个白色方框代表两件事件发生的四种可能情况。
- A 以及 B
- A 但是不是 B
- B 但是不是 A
- 都不是 A 也不是 B
灰色阴影部分表示每个事件的总频次,不考虑重叠,这相当于行和列的总和。基础率来自这些边缘,这就是为什么它们通常被称为边际概率。
接下来,我们就像玩数独那样填空,让每一行每一列的数字都加起来。
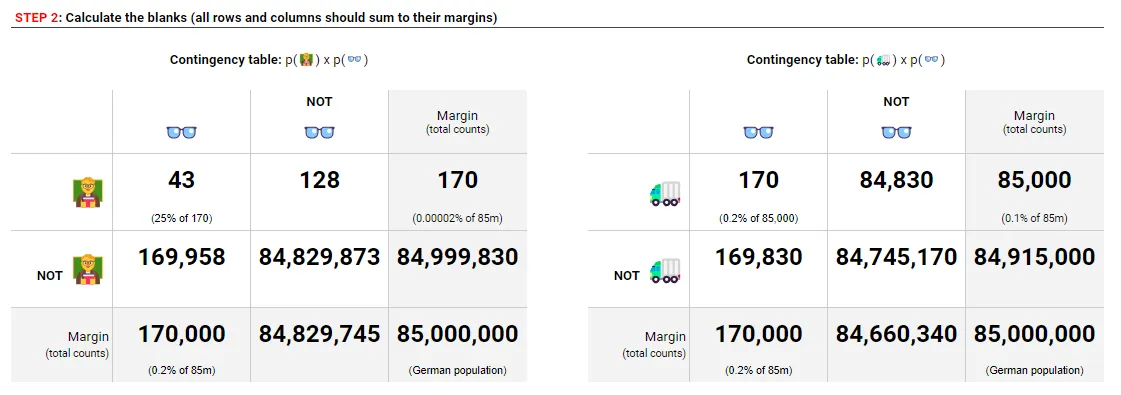
图片和资源由作者制作 - 详见此处
现在,随着我们的列联表完成,我们对基准概率和配置文件符合描述的可能性有了全面的了解。在贝叶斯公式中,所有这类概率现在都能在这里找到,可以按如下方式计算:

这张图片和这些资源都是作者创作的,详见这里
我们感兴趣的概率是上面提到的三个概率中的第三个,即根据这个描述,他们是教授或卡车司机的概率。
而且,根据我们的参数估计,我们看到卡车司机比教授更有可能符合条件,是前者的4倍可能(0.001除以0.00025)。相比之下,这与相反的情况相反,在那种情况下,描述更有可能符合教授的标准,而不是卡车司机的标准,是前者的125倍可能(0.25比0.002)!
回到马尔美西现在,回到我们一开始讨论的马尔梅斯案例,希望你对这种直觉已经有了一定的把握,基率在做出猜测时的重要性已经很清楚了吧。
当我们考虑贝叶斯公式时,实际上就是在比较我们在以下三种情况下的信念程度:
- A 选项是 轻微宿醉 的概率 | B 选项是 malmsey
- A 选项是 女巫的诅咒 的概率 | B 选项是 malmsey
- A 选项是 加强酒 的概率 | B 选项是 malmsey
因为在这种情况下,我们不知道malmsey可能指的是什么(如果我们有一些词源上的猜测,情况就会不同),我们可以说B是没有信息的,因此为了做出合理的猜测,我们只能根据A的概率来做判断。根据贝叶斯公式,我们可以看到,我们感兴趣的这个概率会随着A的基本率变化而变化。

图片为作者所作
为了完整起见,这里是我们对信念概率进行制表时可能的样子,类似于多贝利例子中的列联表。因为B不提供任何信息,我们给了“malmsey”匹配任何其他单词或概念50对50的几率。这有点小题大做,一旦我们认识到可以用基准概率来调整我们对答案的信心,就几乎不需要这样做了。不过这样做的目的是为了展示贝叶斯框架在处理更抽象问题时仍然适用。
忽略基准率在 A/B 测试中我之前写过一篇关于检察官谬误的文章(在该文中提供了其他关于基础率忽视的例子,并探讨了这对数据分析师的意义),这种谬误是一种基础率忽视的形式。
再次强调这一点,在传统A/B测试中,人们常常将测试结果出现的概率与假设为真的概率混淆。关于p值及其陷阱已有大量讨论(例如,参见十二大p值误解),在这种情况下,贝叶斯思维有助于清晰我们的推理,并有助于提高对基础率忽视(即先验)概念的警觉性,即我们对假设为真的初始信念。在这种情况下,我们对假设的_先验信念_在一开始就显得尤为重要。
我鼓励你读一下这篇文章(https://medium.com/how-to-intuit-the-prosecutors-fallacy-and-run-better-hypothesis-tests-2d8561bfc5a6),以更好地把握其中的要点。
重点- 涉及的概念包括:忽略基本率,条件概率与边际概率,贝叶斯公式,列联表(交叉表)。
- 注意不要在日常判断事件发生的可能性时将 p(B|A) 和 p(A|B) 等同起来。
- 判断新观察是否支持你的假设时,不要忽视基本率。
- 新闻我才知道:马尔维纳酒是马德拉岛上的一种加强酒。在莎士比亚的《理查三世》中,乔治·克拉伦斯,克拉伦斯公爵淹死在一桶马尔维纳酒里。
- Rolf Dobelli的《思考,清晰地》 书中包含许多日常生活中常见的思维陷阱,其中包含本文引用的教授与卡车司机之谜。书中第28章关于基础率忽略的内容十分出色,第19章关于回归均值的阐述,第34章关于指数增长的分析,第37章关于错误因果关系的讨论,以及其他许多章节都给我留下了深刻印象。每章内容精炼,仅约2-3页,这本书记载了常见的偏见和谬误,非常适合作为参考手册。
- Michael Lewis的《挽救计划》(《大空头》的作者)讲述了Kahneman,Tversky和行为经济学的发展历程。这本书引人入胜,甚至可能被改编成电影。
- David Spiegelhalter的《统计的艺术》 中包含了易于理解的贝叶斯统计学章节。
- 如何直观理解检察官谬误(并更好地进行假设检验) 是我之前写的一篇文章,当时我正在努力理解和定义p值。
- 要直观理解贝叶斯公式,Stat Quest上的这两个视频推荐观看:1. 条件概率 和 2. 贝叶斯定理。

 随时随地看视频
随时随地看视频




