在复杂的路径模型里,可能会迷失方向。照片由 [Deva Darshan] 提供,来自 [Unsplash]
数据科学家经常收集许多变量并试图找出它们之间的关系。在这个过程中,有假设和猜想是很管用的。学生为下次考试而学习的动力是否会影响他们的成绩?还是说好成绩会激励学生继续努力?究竟什么样的行为模式能让有动力的人取得好成绩呢?
为了给上述类似的问题提供一些结构,并提供一种工具来实证检验这些问题,我将解释路径模型,本文中也称为结构方程模型(SEM)。虽然在社会科学领域,如心理学中路径模型被广泛使用,但我感觉在其他领域,如数据科学和计算机科学中,它们并没有那么突出。因此,我将概述一下路径分析的主要概念,并介绍一个叫做semopy的工具,它是一个在Python中应用路径分析的工具。在本文中,我们将通过分析人工数据来展示路径模型可以解决的典型问题,并介绍调节变量和中介变量。请注意,这些数据是为展示目的而生成的,可能在某些细节上并不完全现实。
研究课题在分析数据前,我们需要知道我们在寻找什么。照片由 Ansia Lasa 拍摄,来自 Unsplash
如果我们想要分析数据,首先需要有一个明确的研究问题。在这篇文章中,我们将研究在校儿童及其成绩。我们可能对促进学习和取得好成绩的因素感兴趣,比如。这可能是他们对学校的乐趣,他们对科目的兴趣,他们在班级里的朋友数量,他们与老师的关系,他们的智力水平等等。因此,我们进入不同学校,分发关于归属感、与老师的关系、对科目的兴趣以及学校乐趣的问卷,我们对学生进行智力测试,并询问他们有多少朋友。当然,我们也会收集他们的考试成绩。
一切始于数据我们现在有了这里列出的所有变量。

接下来,我们要看看这些变量究竟如何影响成绩。我们可以对这些影响做出不同的假设,并且可以通过数据来验证这些假设。让我们从最简单的情况开始,即我们假设每个变量对成绩都有直接的影响,且独立于所有其他变量。例如,我们会假设更高的智力会导致更好的成绩,不管对主题的兴趣或学生在学校是否有乐趣的兴趣或乐趣。对于其他变量,我们也会假设它们与成绩之间存在类似的影响。从视觉上看,这种关系可以表示如下:
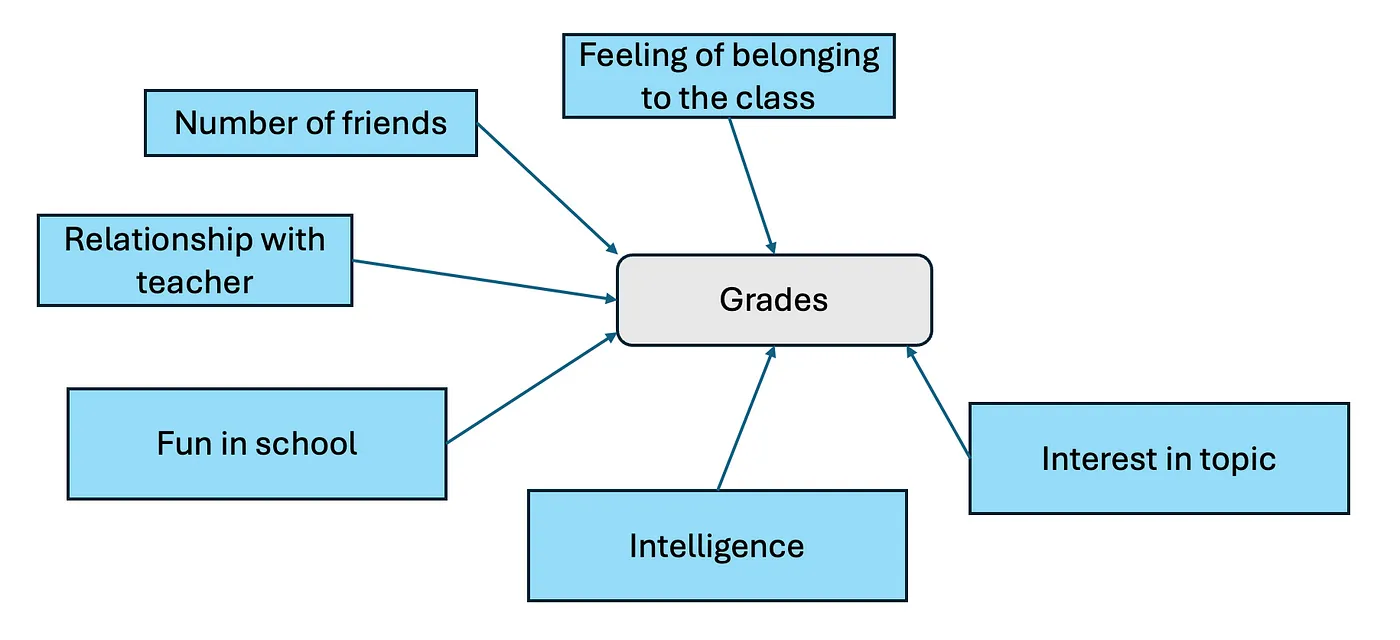
假设所有变量都直接对评分有影响。图片由作者提供。
每个箭头描述着变量间的影响。我们也可以将其表示为加权和,如下。
grades = a归属感 + b朋友数目 + c与老师的相处 + d学校的趣味 + e智力 + f对主题的兴趣
在这里,a, b, c, d, e 和 f 是权重,它们告诉我们,不同的变量对我们的成绩有多大影响。好的,这是我们设定的假设。现在我们想用数据来验证一下这个假设。假设我们有一个名为_data_的数据框,其中包含了上述所有变量的列。然后我们就可以像下面这样使用python中的semopy了:
# 下面的代码保持原样 import semopy
path = """
成绩 ~ 智力 + 对主题的兴趣
+ 归属感 + 与老师的相处
+ 在学校的感觉 + 朋友数
"""
m = semopy.Model(path)
m.fit(data)在最后几行中,我们创建了一个 semopy.Model 对象,并用数据对其进行拟合。最有趣的部分是在前面定义的 path 变量,这里我们指定了我们刚刚提到的假设,即变量 grades 是由所有其他变量组合而成。在波浪线 (~) 的左侧,我们有我们预期会受到波浪线右侧变量影响的目标变量。请注意,我们没有明确指定权重 a, b, c, d, e 和 f。这些权重实际上是我们想找出的,因此让我们运行下面的代码行以得到结果。
m.inspect()注:上述代码未进行翻译,因为它是编程上下文中直接引用的部分,需保持原样以确保准确性和功能性。
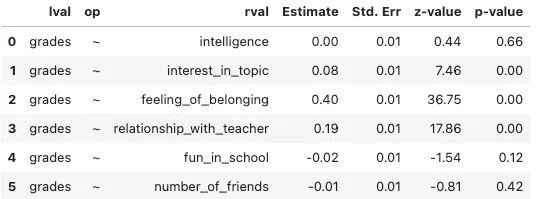
假设所有变量直接影响成绩变量。如下图所示。作者供图。
权重a、b、c、d、e和f就是我们在‘Estimate’列中看到的数值。我们能从这张表格中提取哪些信息呢?首先,我们可以看到一些权重较大,而一些则较小。例如,_feeling_of_belonging_的权重最大(0.40),说明它的影响力最强。相比之下,_Interest_in_topic_的权重则小得多(0.08)。而其他变量,如_intelligence_和_number_of_friends_的权重则几乎为零。
此外,可以看看_p-value_列。如果您熟悉统计检验,您可能已经知道这列怎么读。如果没有,请不要担心。有大量的文献教你如何理解显著性(这就是这一列所指示的内容),我鼓励您深入了解这一主题。然而,就目前而言,我们可以简单地说这一列能给你一些提示,说明找到的影响有多大可能是随机的。例如,_number_of_friends_对成绩的影响非常小(-0.01),并且非常有可能(0.42),这种影响可能是巧合。因此,我们可以认为没有显著影响,尽管权重并不完全为零。相反,如果p值非常接近于零,我们可以认为我们找到了一个并非仅仅是巧合的影响。
好的,根据我们的分析,影响成绩的变量有三个,分别是“对主题的兴趣” (0.08),“归属感” (0.40) 和“师生关系” (0.19)。其他变量没有影响。这就是我们最终的结论吗?
那不一定!请记住,semopy所做的计算受我们给定假设的影响。我们假设所有的变量都是独立的,并直接影响成绩。但实际情况可能完全不同呢?变量之间可能存在许多其他的影响方式,因此让我们提出一些不同的假设,从而探讨中介变量和调节变量的概念。
中间人
调解人可以像台球一样,一个球把另一个球推走。图片来自 Steve Mushero 和 Unsplash
而不是说 _number_offriends 和 _feeling_ofbelonging 都直接影响成绩,让我们换个角度想。如果你在班上没有朋友,你就不会有那种归属感,对吧?这种归属感的缺失可能会进而影响成绩。所以这种关系可能更像这样:
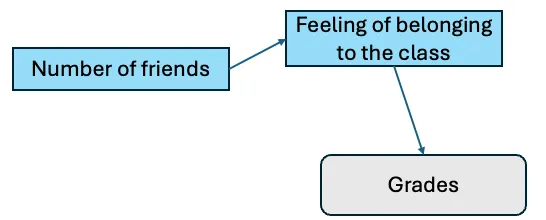
假设朋友数量影响归属感,而归属感又反过来影响成绩。图片来源:作者。
请注意,_number_offriends 对 grades 的直接的影响已经消失了,但我们假设 _number_offriends 对 归属感 有影响,而 归属感 反过来又会影响 grades。我们可以接受这个假设,并让 semopy 来验证一下。
path = """
归属感与朋友数量的关系
成绩与归属感的关系
"""
m = semopy.Model(path) # semopy模型对象
m.fit(data)这里我们说 _feeling_ofbelonging 取决于 _number_offriends,而 grades 取决于 _feeling_ofbelonging。如下所示,_feeling_ofbelonging 和 grades 之间的权重仍然是0.40,而现在在 _number_offriends 和 _feeling_ofbelonging 之间也有 0.29 的权重。看来我们的假设是正确的。朋友数量的影响最终体现在归属感上,而这又会影响成绩。

假设朋友的数量会影响归属感,结果是... 图片由作者提供。
在这里我们所建模的影响类型被称为中介作用,因为一个变量间接影响另一个变量,通过中介变量。换句话说,number_of_friends 并没有直接对成绩产生影响,而是通过归属感间接产生影响。
通过一些变量之间的中介作用,我们可以更清楚地了解它们是如何相互影响的。那些对自己未来有明确目标和规划的学生不太可能从高中辍学,但到底是什么样的行为模式能够让学生在学校里表现出色呢?是学习更多吗?还是在不理解某个话题时去寻求帮助呢?这两种行为都可以是解释明确目标如何影响学业成绩的中介因素。
版主
版主就像一个阀门,只控制一定的流量。图片来源:Igal Ness在Unsplash提供
我们刚刚看到,假设变量之间存在不同的关系有助于更有效地描述数据。也许我们也可以采用类似的方法来解释在我们的数据中,智力对成绩没有直接影响的现象。这听起来很令人惊讶,不是吗?因为通常我们期望更聪明的学生会取得更高的成绩。然而,如果一个学生对某个主题不感兴趣,他们就不会花太多时间去努力,不是吗?也许智力对成绩并没有直接的影响,但智力和兴趣的结合却可能对成绩产生影响。如果学生们对主题感兴趣,更聪明的学生通常会取得更高的成绩,但如果他们不感兴趣,就可能不会有太大的影响,因为他们可能不会投入太多精力。我们可以像这样来可视化这种关系。
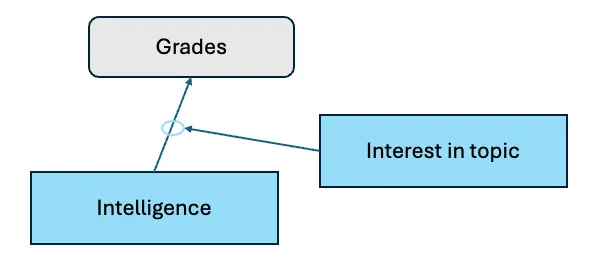
假设兴趣对主题的兴趣可以调节智力对成绩的影响。图作者提供。
也就是说,我们假设 智力 对 成绩 有影响,但这种影响受到 对这个科目的兴趣 的影响。如果兴趣高,学生或者孩子就能更好地发挥他们的智力,从而取得更高的成绩,但如果兴趣低,他们可能就表现平平。
如果我们想在semopy中测试这个假设的话,我们需要创建一个新的变量,它是_intelligence_和_interest_in_topic_的乘积。你看,这样乘法不就反映了我们刚才的想法了吗?如果_interest_in_topic_接近于零,那么整个乘积也几乎为零,不管_intelligence_的值是多少。但如果_interest_in_topic_很高,那么乘积主要取决于_intelligence_的大小。因此,我们在数据帧中计算新的一列,将其命名为_intelligence_xinterest,我们称它为“智力乘兴趣”,并用我们假设的该变量与成绩之间的关系来输入给semopy。
path = """
智力和兴趣对成绩值的影响 ~ 智力 _ x _ 兴趣
"""
m = semopy.Model(path)
m.fit(数据)我们还发现了一个效果,

这是假设智力与兴趣的乘积会影响成绩的结果。图片由作者提供。
之前,成绩 并未受到 智力 的影响,而 对这个话题的兴趣 的影响也非常小(仅为0.08)。但是如果我们把两者结合起来,我们却发现了非常大的影响,达到了0.81。看来这两者的结合更好地解释了我们的数据。
这种变量之间的相互作用被称作调节作用。我们会说,_interest_in_topic_调节了_intelligence_对_grades_关系的影响,因为_intelligence_与_grades_之间的联系强度取决于兴趣。调节作用有助于我们理解变量间的关系在不同情境或不同参与者群体间如何有所不同。例如,工作经验对薪水有正面影响,但对于男性来说,这种影响比女性更强一些。在这种情况下,性别便成了调节工作经验对薪水影响的因素。
总结一下结合所有之前的步骤,我们的新模型就是这样。

包含所有先前假设的完整模型。作者提供图片。
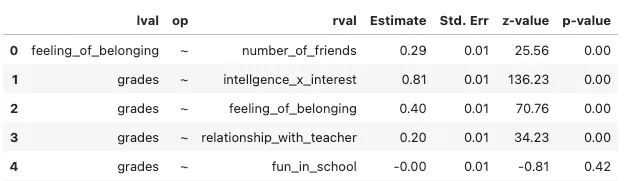
完整模型的结果。作者制作的图片。
我们现在有一个更复杂且更合理的数据结构。请注意,_fun_inschool 仍然不会对 grades 产生影响(因此我在上面的可视化中用虚线表示它)。这可能是因为数据中确实没有这种影响,或者我们还没有找到与其他变量的正确互动方式。我们甚至可能还缺少一些有趣的变量。就像 intelligence 只有与 _interest_intopic 结合才有意义一样,也许还有一个变量是理解 _fun_inschool 对成绩影响的关键。这说明,对于路径分析而言,理解数据以及你想研究的问题是很重要的。这一切都始于从理论(或有时是直觉)中得出的假设,并用数据来验证这些假设,以便更好地理解数据。
这就是路径模型所讲的内容。我们来总结一下刚才学到的内容吧。
- 路径模型允许我们测试变量之间如何相互影响的假设。
- 中介效应出现,当变量 a 不直接对变量 c 产生影响,而是影响另一个变量 b ,然后 b 再影响 c 。
- 如果变量 a 对变量 c 的影响依赖于变量 b 的值而变强或变弱,我们就称之为 调节效应。这可以通过计算变量 a 和 b 的乘积来建模。
- Semopy 可以在 Python 中使用给定的数据来测试路径模型。
我希望我已经让你相信路径模型的有用性。不过我所展示的只是刚刚开始。还有许多更复杂的假设可以通过路径模型或其他相关模型来检验,这些内容远远超出了本文的讨论范围。
参考你可以在这里找到semopy。
如果你想了解更多关于路径分析法的信息,维基百科可以是一个很好的起点。
我用这本书作为统计背景知识(不幸的是,这本书只提供德文版)
- 艾德,M.,戈利茨,M.,与施密特,M. (2015,). 统计学与研究方法。(著作)
本文的数据就是这样来的。
import numpy as np
import pandas as pd
np.random.seed(42)
N = 7500
def norm(x):
return (x - np.mean(x)) / np.std(x)
number_of_friends = [int(x) for x in np.random.exponential(2, N)]
# 假设这里问卷的范围是0到5
relationship_with_teacher = np.random.normal(3.5,1,N)
relationship_with_teacher = np.clip(relationship_with_teacher, 0,5)
fun_in_school = np.random.normal(2.5, 2, N)
fun_in_school = np.clip(fun_in_school, 0,5)
# 假设关于主题的兴趣问卷的范围是从0到10
interest_in_topic = 10-np.random.exponential(1, N)
interest_in_topic = np.clip(interest_in_topic, 0, 10)
intelligence = np.random.normal(100, 15, N)
# 将变量归一化
interest_in_topic = norm(interest_in_topic)
fun_in_school = norm(fun_in_school)
intelligence = norm(intelligence)
relationship_with_teacher = norm(relationship_with_teacher)
number_of_friends = norm(number_of_friends)
# 创建依赖变量
feeling_of_belonging = np.multiply(0.3, number_of_friends) + np.random.normal(0, 1, N)
grades = 0.8 * intelligence * interest_in_topic + 0.2 * relationship_with_teacher + 0.4*feeling_of_belonging + np.random.normal(0,0.5,N)
data = pd.DataFrame({
"成绩":grades,
"智力":intelligence,
"朋友数量":number_of_friends,
"学校乐趣":fun_in_school,
"归属感": feeling_of_belonging,
"兴趣":interest_in_topic,
"智力_x_兴趣" : intelligence * interest_in_topic,
"与老师的关系":relationship_with_teacher
})喜欢这篇文章吗?关注我吧 以便及时收到我未来文章的推送。

 随时随地看视频
随时随地看视频




