作为一种自然界中普遍存在的一种现象,布朗运动指的是颗粒在介质中(通常是气体或液体)进行的随机运动。这种现象最初是由植物学家罗伯特·布朗在1827年通过显微镜观察浸在水中的花粉粒时发现的。大约再过了八十年,科学家们才对这一现象建立了深刻的定量理解。值得一提的是,阿尔伯特·爱因斯坦的贡献为与扩散关联的布朗运动奠定了坚实的理论框架 [1, 2]。
简单来说,布朗运动的思想是轨迹是随机且不可预测的。这一思想已被广泛应用于多个科学和应用领域,其中包括金融量化,用于描述股票价格变动的随机行为。在这个故事里,我们将用Python来做基于布朗运动的股票价格模拟。
通常称为标准布朗运动(维纳过程)请注意:本文仅供教育用途,不构成任何投资、财务或其他专业建议。
股票价格的随机性依赖于每日回报率几乎符合正态分布的经验观察。这一现象背后的推动力是标准布朗运动,也就是维纳过程。对于时间 t 的股票价格变化增量 {W(t) : t ≥ 0},维纳过程具有以下特点:,
- 它从零点开始,即 W(0) = 0。
- 对于任意时间步长 dt,后续增量与当前增量之差遵循 正态分布:W(t +dt) - W(t) ~ N(0, dt)
- W(t) 的变化是连续的。
下面是一个在 Python 中实现 W(t) 的示例,以及一个可能的变化过程的图像。
import numpy as np
import numpy.random as npr
import matplotlib.pyplot as plt
# 用于计算W随时间演化的函数(例如,n=1000个时间步)
def wiener_process(dt=0.1, x0=0, n=1000):
# 初始化W
W = np.zeros(n+1)
# 生成从0到n的n+1个时间点
t = np.linspace(x0, n, n+1)
# 通过累积求和来计算每个时间步的W值
W[1:n+1] = np.cumsum(npr.normal(0, np.sqrt(dt), n))
return t, W
# 绘制W过程的函数
def plot_process(t, W):
plt.plot(t, W)
plt.xlabel('时间 t')
plt.ylabel('W(t)')
plt.title('维纳过程图')
plt.show()
t, W = wiener_process()
plot_process(t, W)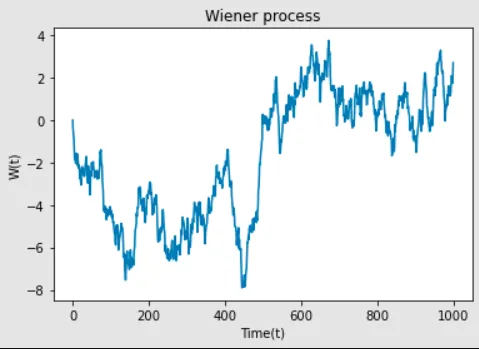
图1:根据上述Python脚本计算得出的可能轨迹W(t _ )。
股票价格行为由算术布朗运动模型描述根据维纳过程的上述特点,它理论上可以代表股票每日的价格波动,而不考虑任何看涨或看跌的趋势,即价格的上升或下降趋势。然而,由于实际股票市场不会出现这种情况,我们也需要考虑一个确定的成分,即所谓的漂移,在看涨趋势下它是正的,在看跌趋势下它是负的。
这样想来,股价在时间 (t) 时记为 (S(t)),在时间跨度 (dt) 内,(S(t)) 的变化为 (dS),可以表示为:
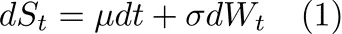
这代表了一个 算术布朗运动模型。如下所示,从方程 (1) 可以看出,两个关键量进入了确定性部分和随机部分的表达式。
- 平均收益 μ 导致漂移
- 风险/波动率 σ 与维纳过程相关的随机波动
如方程 (1) 所示,S(t) 的定性描述如图 2
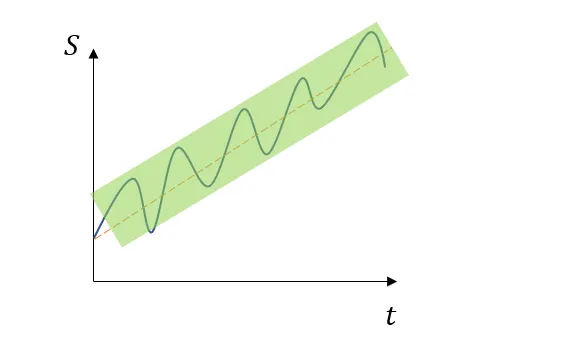
图2:股票价格的演变S(t)(实线)的示意图,在算术布朗运动模型下。线性部分代表漂移项(虚线部分),而随机部分则源自描述价格波动的维纳过程(绿色阴影区域)。
不过,公式 (1) 的一个缺点是,在此模型中股票价格可能会跌到负值。由于这种情况在现实中从未发生过,因此我们需要使用公式 (1) 的另一个版本,在这个版本中,股票遵循的是对数正态分布而不是正态分布。这可以通过 几何布朗运动 来实现。
股价模拟分析与几何布朗运动模型几何布朗运动具有以下特征等等。
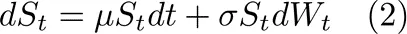
如下解法:
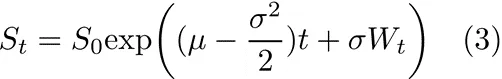
在这个形式下,由于 S(t) 遵循对数正态分布,股票价格始终保持非负。我们现在可以用方程 (3) 和以下参数模拟股票价格的变化。
- S<sup>0</sup>=S<sub>0</sub>=10 $
- μ=0.1
- σ=0.05
在时间范围 [0, T] 内(默认情况下 T = 1),根据下面这个 .py 脚本:
import numpy as np
import numpy.random as npr
import matplotlib.pyplot as plt
def simulate_geometric_brownian_motion(initial_stock_price, T=1, N=1000, mu=0.1, sigma=0.05):
# 设置时间步长 dt
dt = T/N
# 初始化随机漫步 W(t)
W = np.zeros(N+1)
# 创建 N 个时间步
t = np.linspace(0, T, N+1)
# 使用累积和来计算每个时间步上的 W 值
W[1:N+1] = np.cumsum(npr.normal(0, np.sqrt(dt), N))
# 计算股票价格 S(t)
stock_prices = initial_stock_price * np.exp((mu - 0.5 * sigma ** 2) * t + sigma * W)
return t, stock_prices
def plot_simulation(t, stock_prices):
plt.plot(t, stock_prices)
plt.xlabel('时间')
plt.ylabel('股票价格')
plt.title('股票价格的几何布朗运动模拟')
plt.show()
# 使用初始股票价格 S0 = 10 美元来计算股票价格
[t, stock_prices] = simulate_geometric_brownian_motion(10)
plot_simulation(t, stock_prices)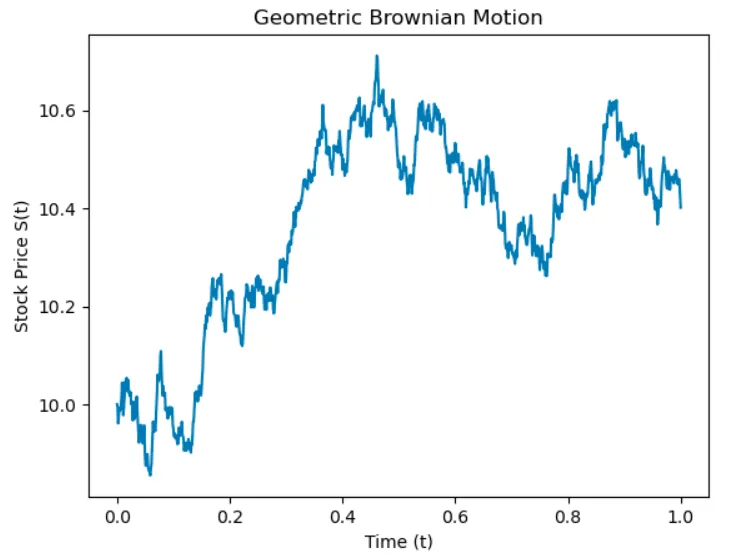
使用公式(3)并设置参数S0 = 10美元,μ = 0.1,σ = 0.05来模拟股票价格路径。
为了确认_(S(t))是否真正符合对数正态分布,具体来说,需要模拟许多条几何布朗运动的轨迹,并绘制(S(t))_的分布图。这可以通过强大的Python库Aleatory来验证,它能够模拟并可视化随机过程[3]。
使用 Aleatory 模拟几何布朗运动的过程注:Aleatory 是指与随机性相关的概念。
该模拟非常简单,因为在上述 .py 脚本中执行的所有过程都在 Aleatory 中的一个名为 GBM 的类中实现。使用任何开发环境,例如 Jupyter Notebook,都可以通过创建一个 GBM 实例来完成。
# 安装 aleatory(如果需要)
pip install aleatory
# 导入几何布朗运动类 GBM
from aleatory.processes import GBM
# 创建 GBM 对象的实例
几何布朗运动对象 = GBM(drift=1, volatility=0.5, initial=1.0, T=1.0, rng=None)以下参数,默认使用 T = 1,如下所示。
- 这里,S ₀ 设定为 1 $
- 这里,μ 设定为 1
- 这里,σ 设定为 0.5
(注:σ 和 μ 是常用的统计学符号,分别表示标准差和均值。此处的 "$" 符号用于表示特定的数学含义,而非货币单位。)
最后一个条目指的是随机数生成器的种类,默认为 None。因此,可以使用 draw 方法绘制图表。
绘制了100个点,共200步的几何布朗运动其中 n c 表示每个轨迹中的步骤数,而 N 则表示需要模拟的轨迹数量。

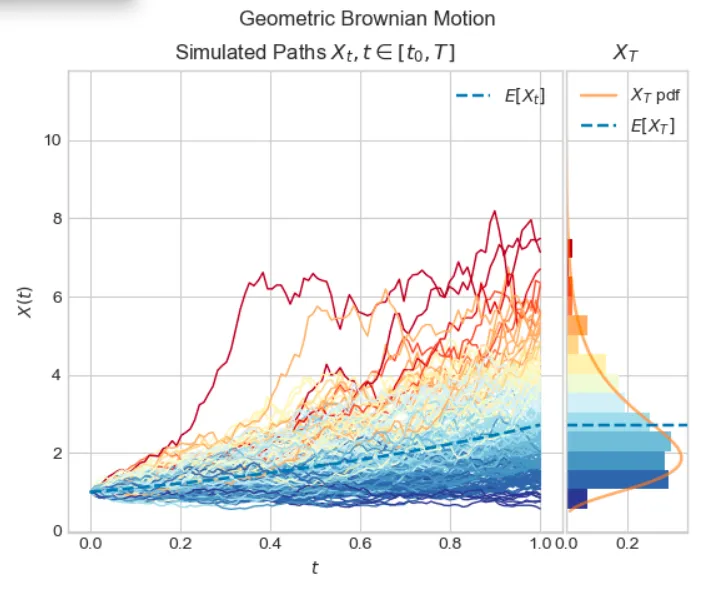
图4:使用Aleatory软件包模拟的股票价格走势(主图),以及在T=1点的分布(右图)
如图4所示的模拟,生成了若干条股票价格走势,其呈对数正态分布,这一点从其明显的偏斜可以看出来。
结论部分总之,使用布朗运动来模拟股票价格走势可以提供对市场动态以及股票潜在未来趋势的深入了解。虽然Python的Aleatory库提供了广泛的工具来进行此类模拟,但也需要注意,布朗运动只是股票波动的一个简化模型,它并不能捕捉到实际市场中的所有重要因素(如经济事件、利率变化等)。然而,结合进一步分析和实证数据,布朗运动是金融市场中做出明智决策的理想工具。
参考文献[1] 阿尔伯特·爱因斯坦, Ann. Phys.Vol. 17, 549 (1905).
[2] A. 爱因斯坦, 《电化学与物理化学杂志》 第13卷, 页41 (1907),

 随时随地看视频
随时随地看视频




