
变分自动编码器(VAEs)是一种生成式AI模型,因其能够生成逼真的图像而引起了人们的注意,但它们也可以生成引人注目的时间序列数据。标准的VAE可以被调整以捕捉时间序列数据中的周期性和序列性模式,然后用于生成可信的模拟。我建立的模型使用1-D卷积层、策略性的步长选择、灵活的时间轴和季节性相关的先验分布来模拟温度数据。
目标我利用了亚利桑那州凤凰城过去50年的[每小时ERA5温度数据]来训练模型。为了生成有用的数据,该模型必须捕捉原始数据的几个关键特征:
- 季节特征 — 夏天应该比冬天更温暖
- 昼夜特征 — 白天应该比夜晚更温暖
- 自相关性 — 数据应该平滑,连续几天的温度应该保持相似
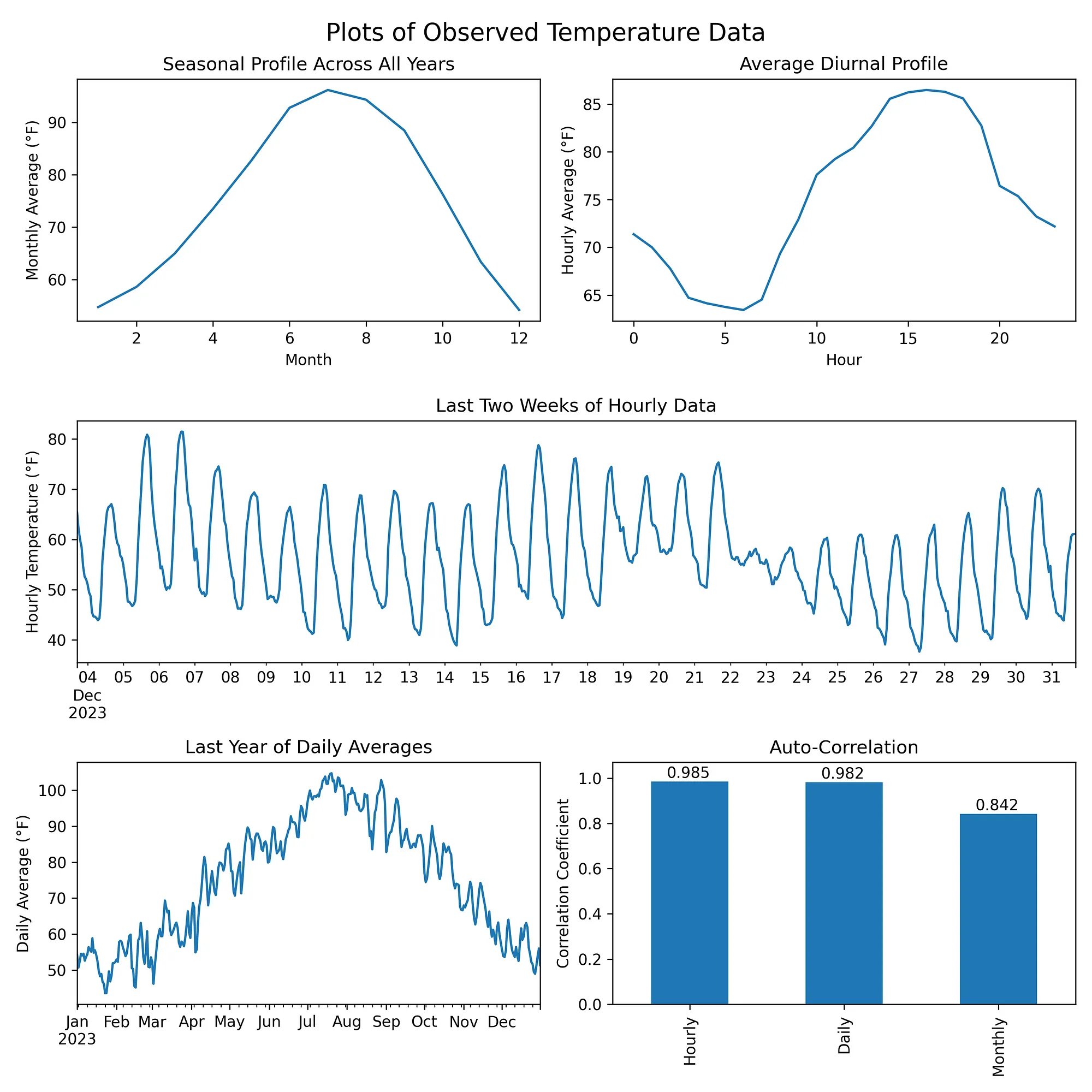
包含经过修改的哥白尼气候变化服务信息(2024年)
气候变化的影响该模型在训练数据没有长期趋势的情况下表现最佳。然而,由于气候变化,温度每十年上升约0.7 °F——这一数值源自观察到的数据,并与发布的地图所示的近期各地区的升温趋势一致的观察数据[2]。为了消除这种升温趋势,我将原始观测值每十年减少了0.7 °F,进行了线性变换。这种调整后的数据集代表了假设2024年的气候条件,历史气温可能的样子。解释这些生成的数据时,应考虑到这一点。
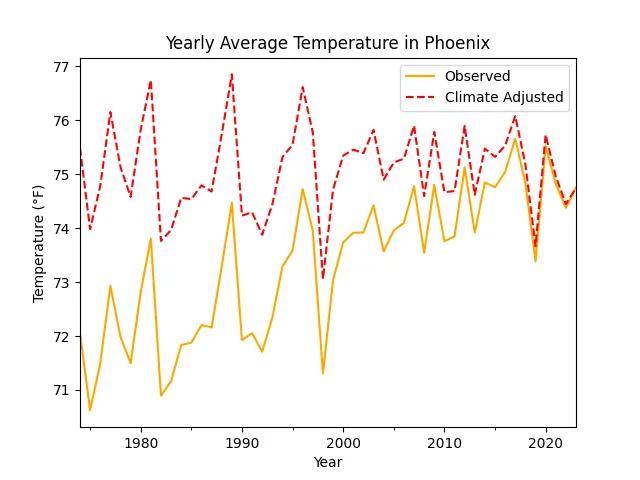
包含修改后的哥白尼气候变化服务信息 [2024]
什么是VAE?(变分自动编码器)变分自编码器(VAE)将输入数据的维度降低到一个更小的潜在空间。VAE定义了一个编码器,用于将观察到的输入转换为称为潜在变量的压缩形式。然后,一个不同的解码器试图重建原始数据。编码器和解码器被共同优化,以尽量减少信息丢失。
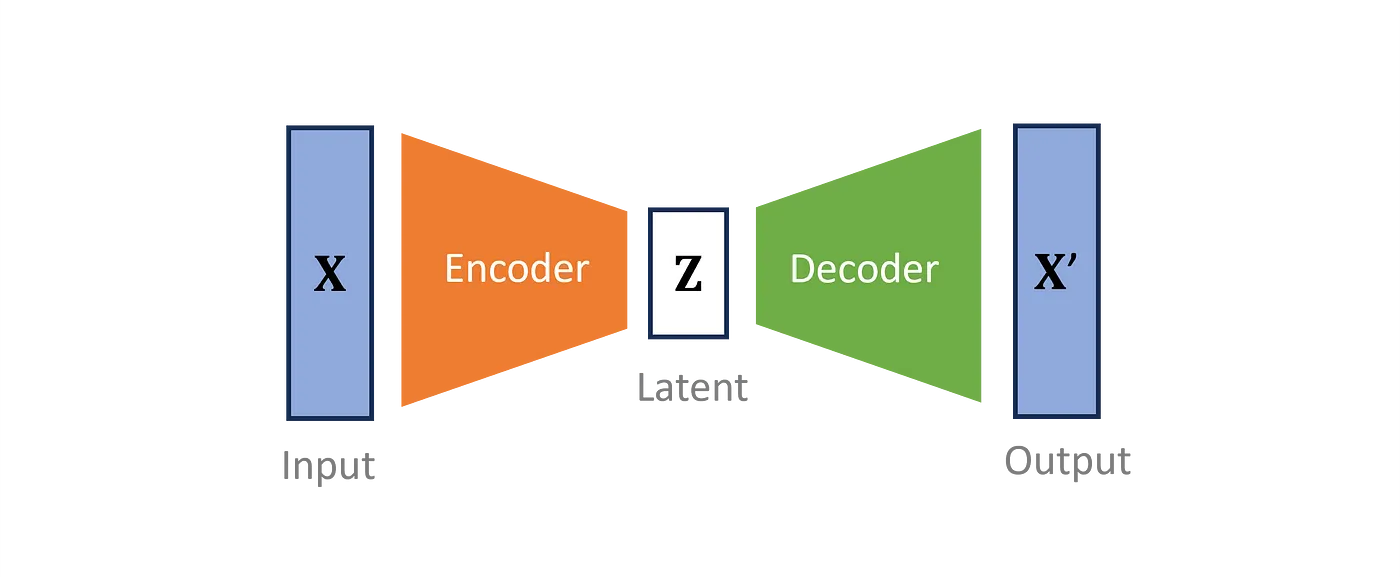
训练过程中使用的完整损失函数包括:
- 一个 重建损失:衡量经过往返变换后的数据与原始输入的匹配程度
- 一个 正则化项:衡量潜在变量的编码分布与先验概率分布的匹配程度
这两个损失项是通过变分推理推导出来的,目的是通过尝试最大化观察数据的证据下界(ELBO)。请参阅此视频的数学推导 [3]: this video
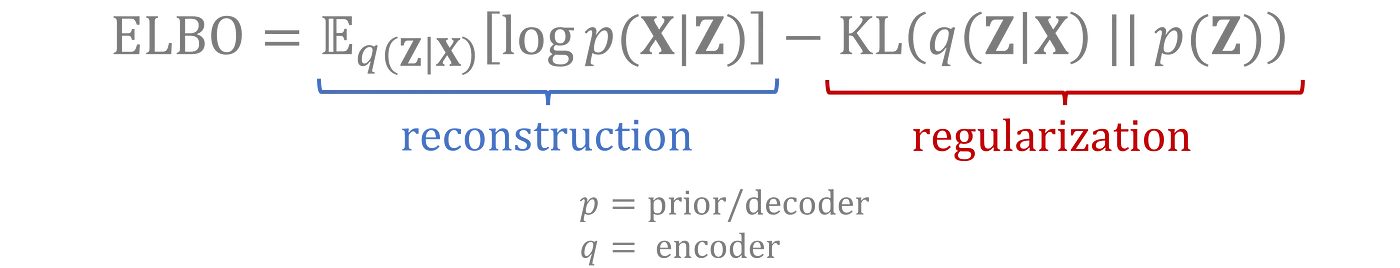
直观地讲,VAE 在训练数据上执行特征提取操作,使得这些特征(通过潜在变量表示)能够符合预先定义的分布。新数据通过从潜在分布中采样,再解码成与原始输入相似的形式生成。
请查阅 Joseph Rocca 的文章,《理解变分自编码器》(Understanding Variational Autoencoders)[4],以获得 VAE 工作原理的详细解释。
一维卷积层为了对凤凰城温度数据进行建模,我将编码器设计为一个包含一维卷积层的神经网络。每个卷积层都会将一个核——即权重矩阵——应用于输入的移位窗口。由于同一个核在整个输入中使用,卷积层被认为是移位不变的特性,并且非常适合具有重复序列模式的时间序列。

左:卷积层的矩阵运算表示 | 右:图形表示 | 通常,输入和输出通常具有多个特征变量。为了简化起见,矩阵运算展示了输入和输出之间只有一个特征的卷积情况。
解码器执行与编码器相反的任务,使用一维转置卷积层,也称为转置卷积层。潜在特征被投影到重叠序列中,以生成一个与输入高度吻合的输出时间序列。
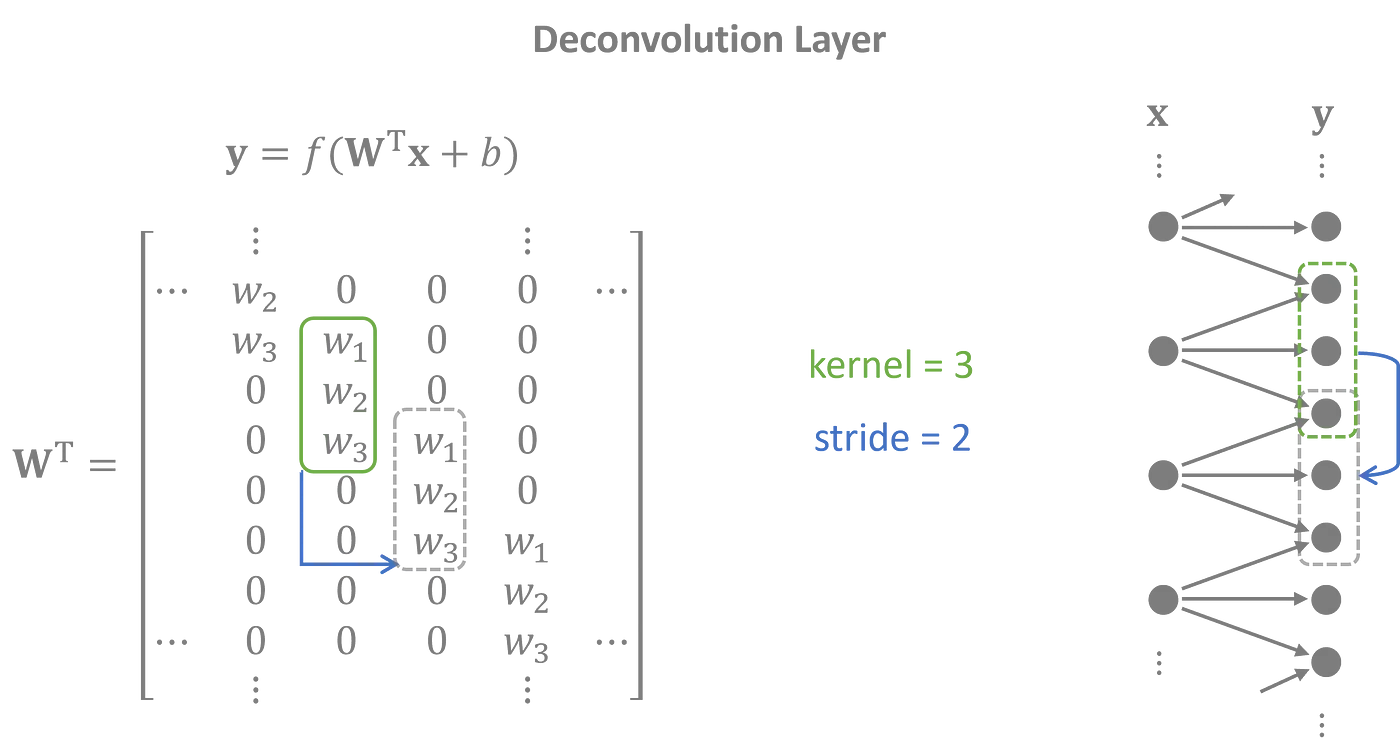
反卷积层的权重矩阵是卷积层权重矩阵的转置。
该完整模型将多个卷积和反卷积层堆叠在一起。每个中间隐藏层扩展了潜在变量的范围,使模型能够捕捉数据中的长距离效应。

步幅——移位之间的跳跃——决定了下一个层次的大小。卷积层使用步幅来减小输入的尺寸,而反卷积层使用步幅将潜在变量扩展回输入尺寸。然而,它们还具有次要的作用——捕捉时间序列中的周期性趋势。
可以策略性地选择卷积层的步幅以复制数据中的周期性模式。
卷积通过周期性地应用核,以步幅为周期重复使用相同的权重。这为训练过程提供了灵活性,可以根据输入在周期中的位置来自定义权重。
将多个层堆叠在一起会形成一个由嵌套的子卷积层构成的更长的有效周期。
考虑一个将每小时的时间序列数据提炼成特征空间的卷积网络,该空间每天有四个变量分别代表早晨、下午、傍晚和夜晚。具有步幅为4的层将为每天的每个时间段分配独特的权重,以捕捉隐藏层中的昼夜变化特征。在训练过程中,编码器和解码器学习权重以复制数据中发现的每日循环模式。
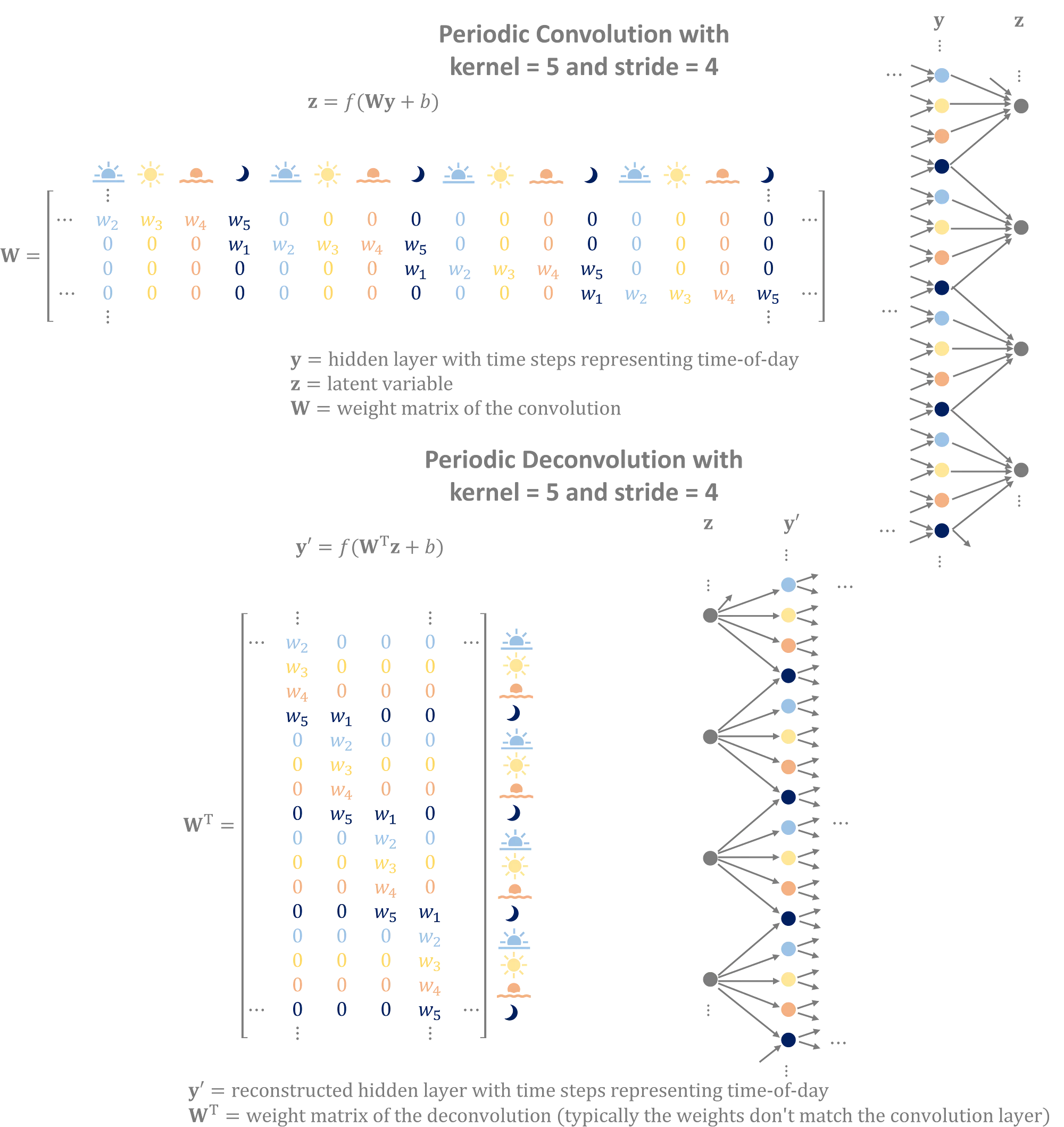
卷积利用输入的周期性以构建更优质的潜在特征。反卷积将潜在特征转换成重叠且重复的序列,以生成具有周期性模式的数据输出。
灵活的时间概念生成图像的VAE通常会用数千张预处理为具有固定宽度和高度的图像进行训练。生成的图像将具有与训练数据相同的宽度和高度。
对于凤凰数据集,我只有一个50年的时间序列。为了改进训练,我将数据拆分为序列,最终决定为每个96小时的时段分配一个潜在变量。然而,我可能希望生成比4天更长的时间序列,并且理想情况下,输出应该是平滑的,而不是在模拟中呈现出明显的96小时分段。
幸运的是,Tensorflow 允许你在神经网络中指定未约束的维度。就像神经网络可以处理任何批次大小一样,你可以构建模型来处理任意数量的时间步长。因此,我的潜变量也包括一个可以变化的时间维度。在我的模型中,输入中的每96小时在潜在空间中对应一个时间步长。
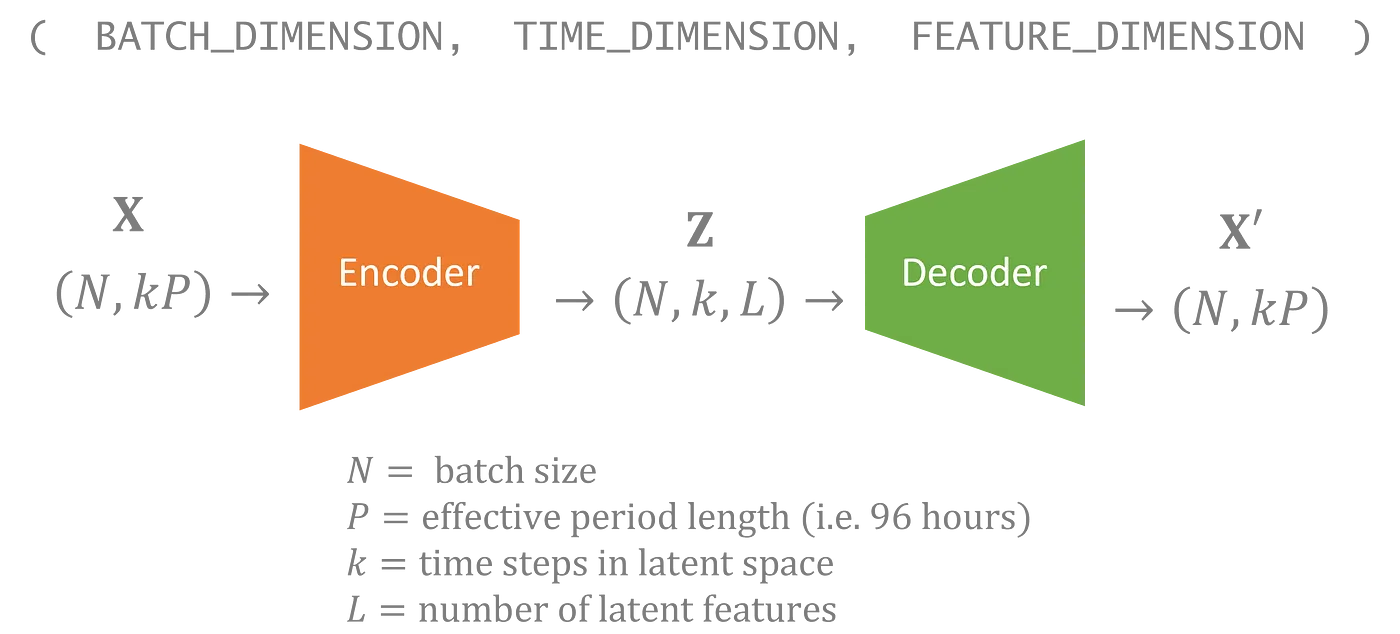
生成新数据就像从先验分布中采样潜在变量一样简单,您可以选择在时间维度上包含的步骤数量。
具有不受限制的时间维度的VAE可以生成任意长度的序列数据。
模拟输出将会有你采样的每个时间步长对应的4天,并且结果会显得平滑,因为卷积层使得输入层的信息可以扩散到相邻的时间段。
季节性依赖的先验在大多数变分自编码器(VAE)中,假设隐变量(latent variable)的每个分量都服从标准正态分布。这种分布,有时也被称为先验分布,通过采样并解码来生成新的数据。在这种情况下,我选择了一个稍微更复杂的先验分布,它依赖于一年中的特定时间。
从季节性先验分布中采样的潜变量将生成特征会随时间变化,反映出一年中不同时间段的数据。
在此前提下,一月的数据与七月的数据将有很大不同,而同一个月生成的数据将具有许多特征。
我将一年中的时间表示为一个角度,θ,其中0°是1月1日,180°是7月初,360°又回到了1月。先验分布是一个正态分布,其均值和对数方差分别为一个关于_θ_的三次三角多项式,多项式的系数是在训练过程中与编码器和解码器一起学习得到的参数。
先验分布的参数是 θ 的周期函数形式,而具有良好性质的周期函数可以使用次数足够高的三角多项式以任意所需的精度进行近似。[5]
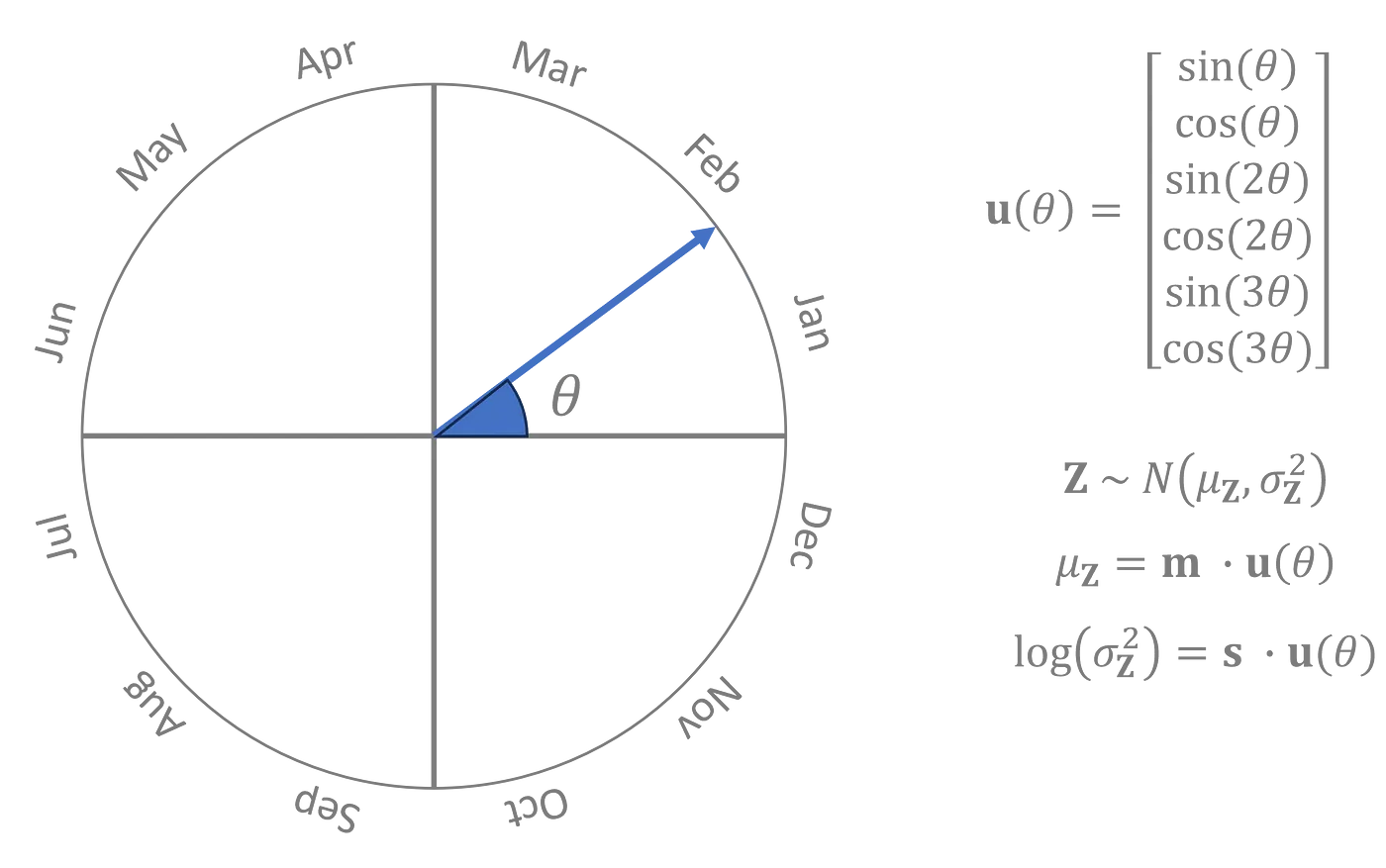
左:_θ 的可视化图 | 右:以参数 m 和 s 表示的 Z 的先验概率分布图
季节数据仅用于先验阶段,并不影响编码器和解码器。这里通过图形方式展示了所有概率依赖关系的完整集合。
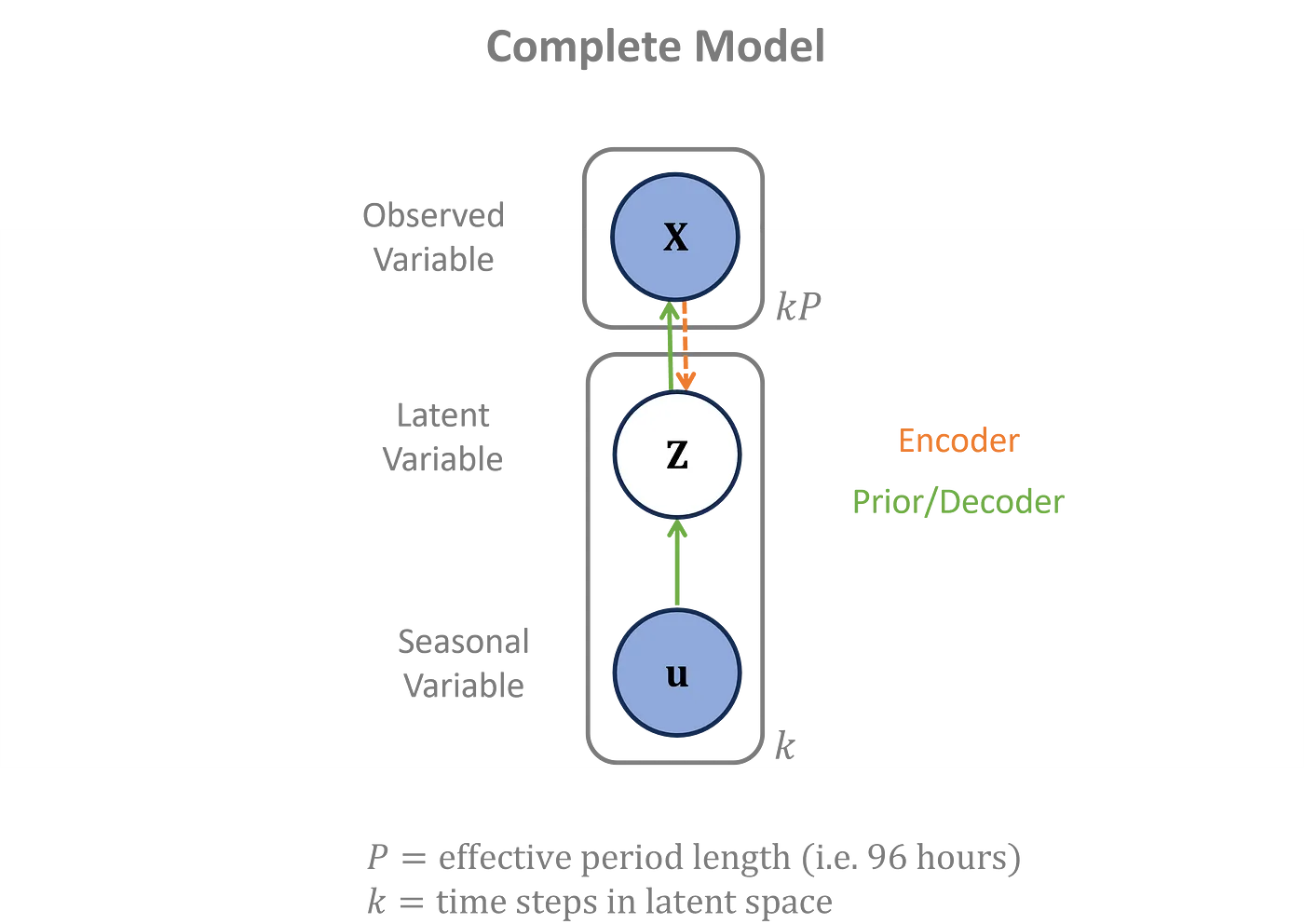
概率图模型,包括先验
实施我使用Python中的TensorFlow来训练模型。
从 tensorflow.keras 中导入 layers 和 models输入的时间维度是灵活的。在Keras中,你使用None来表示一个未指定长度的维度。
使用 'same' 填充会在输入层周围添加零,使得输出大小与输入大小除以步幅相匹配。
inputs = layers.Input(shape=(None,)) # (N, 96*k)
x = layers.Reshape((-1, 1))(inputs) # (N, 96*k, 1)
# Conv1D 参数:filters, kernel_size, strides, padding, dilation_rate
x = layers.Conv1D(40, 5, 3, 'same', activation='relu')(x) # (N, 32*k, 40)
x = layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 16*k, 40)
x = layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 8*k, 40)
x = layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 4*k, 40)
x = layers.Conv1D(40, 3, 2, 'same', activation='relu')(x) # (N, 2*k, 40)
x = layers.Conv1D(20, 3, 2, 'same')(x) # (N, k, 20)
z_mean = x[: ,:, :10] # (N, k, 10)
z_log_var = x[:, :, 10:] # (N, k, 10)
z = Sampling()([z_mean, z_log_var]) # 自定义的采样层从高斯分布中抽取样本
encoder = models.Model(inputs, [z_mean, z_log_var, z], name='encoder')Sampling() 是一个自定义层(custom layer),从具有给定均值和对数方差的正态分布中采样数据。
反卷积操作通过 Conv1DTranspose 进行。
# 输入形状:(批次大小, 时间长度除以96, 潜在特征)
inputs = layers.Input(shape=(None, 10)) # (N, k, 10)
# Conv1DTranspose 参数:filters, kernel_size, strides, padding
x = layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(inputs) # (N, 2*k, 40)
x = layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 4*k, 40)
x = layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 8*k, 40)
x = layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 16*k, 40)
x = layers.Conv1DTranspose(40, 3, 2, 'same', activation='relu')(x) # (N, 32*k, 40)
x = layers.Conv1DTranspose(1, 5, 3, 'same')(x) # (N, 96*k, 1)
outputs = layers.Reshape((-1,))(x) # 输出形状:(N, 96*k)
decoder = models.Model(inputs, outputs, name='decoder') # 解码器模型之前的预设是输入已经形式为[sin(θ), cos(θ), sin(2 θ), cos(2 θ), sin(3 θ), cos(3 θ)]。
Dense 层没有偏置项,以此防止先验分布远离零值过远或整体方差过高或过低。
# 季节性输入的形状为:(N, k, 6)
inputs = layers.Input(shape=(None, 2*3))
x = layers.Dense(20, use_bias=False)(inputs) # 形状为:(N, k, 20)
z_mean = x[:, :, :10] # 形状为:(N, k, 10)
z_log_var = x[:, :, 10:] # 形状为:(N, k, 10)
z = Sampling()([z_mean, z_log_var]) # 形状为:(N, k, 10)
prior = models.Model(inputs, [z_mean, z_log_var, z], name='seasonal_prior')损失函数包含一个重建项和一个潜在变量的正则化项。
函数 log_lik_normal_sum 用于计算观测数据在给定重构输出下的正态对数似然值。计算对数似然需要围绕解码输出的噪声分布,该分布假设为正态分布,其对数方差由 self.noise_log_var 参数表示。在训练过程中学习到的 self.noise_log_var 表示噪声分布的假设。
正则化项方面,kl_divergence_sum 计算两个高斯分布之间的 Kullback–Leibler 散度——具体来说,是隐含编码的高斯分布和先验的高斯分布之间。
class VAE(models.Model):
def __init__(self, encoder, decoder, prior, **kwargs):
# 初始化VAE模型
super(VAE, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
self.prior = prior
self.noise_log_var = self.add_weight(name='var', shape=(1,), initializer='zeros', trainable=True)
@tf.function
def vae_loss(self, data):
# 计算VAE损失
values, seasonal = data
z_mean, z_log_var, z = self.encoder(values)
reconstructed = self.decoder(z)
reconstruction_loss = -log_lik_normal_sum(values, reconstructed, self.noise_log_var)/INPUT_SIZE
seasonal_z_mean, seasonal_z_log_var, _ = self.prior(seasonal)
kl_loss_z = kl_divergence_sum(z_mean, z_log_var, seasonal_z_mean, seasonal_z_log_var)/INPUT_SIZE
return reconstruction_loss, kl_loss_z
def train_step(self, data):
# 训练步骤
with tf.GradientTape() as tape:
reconstruction_loss, kl_loss_z = self.vae_loss(data)
total_loss = reconstruction_loss + kl_loss_z
gradients = tape.gradient(total_loss, self.trainable_variables)
self.optimizer.apply_gradients(zip(gradients, self.trainable_variables))
return {'loss': total_loss}要查看完整实现代码,请访问我的GitHub页面https://github.com/davidthemathman/vae_for_time_series。
结果部分训练后的模型生成的数据与原始温度数据的季节性和日周期性特征以及自相关性相匹配。
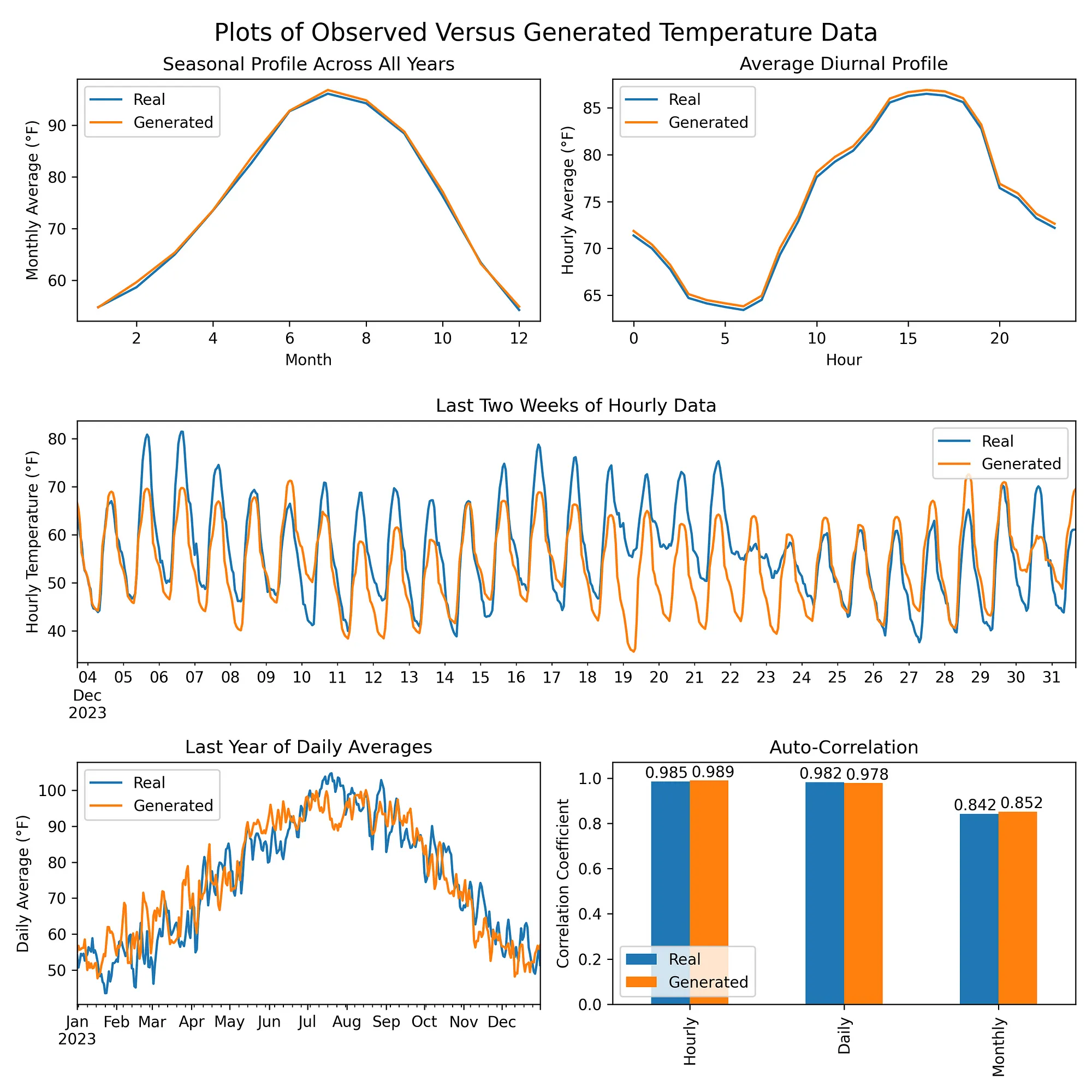
包含经修改的哥白尼气候变化服务中心信息 [2024]
结论:生成时间序列模型的构建技术是一个关键领域,其应用远不止于数据模拟。本文中提到的方法可以适应数据填补、异常识别和预测建模等应用。
通过使用1-D卷积层、战略性步长、灵活的时间输入和季节性先验,你可以构建一个VAE来复制时间序列中的复杂模式。让我们合作来完善时间序列建模的最佳实践。
在评论中分享您关于VAE和/或生成式AI模型在时间序列上的任何经验、疑问或见解。
除非另有声明,所有图片均由作者创作。
[1] Hersbach, H., Bell, B., Berrisford, P., Biavati, G., Horányi, A., Muñoz Sabater, J., Nicolas, J., Peubey, C., Radu, R., Rozum, I., Schepers, D., Simmons, A., Soci, C., Dee, D., Thépaut, J-N. (2023): ERA5 每小时单层数据,自 1940 年至今。Copernicus 气候变化服务中心 (C3S) 气候数据存储 (CDS),DOI: 10.24381/cds.adbb2d47 (2024年8月1日访问)
Lindsey, R., & Dahlman, L. (2024年1月18日). 全球温度变化。Climate.gov。https://www.climate.gov/news-features/understanding-climate/climate-change-global-temperature
[3] Sachdeva, K. (2021, 1月26日). 证据下界(ELBO)— 清晰解释! [视频资料]. YouTube. https://www.youtube.com/watch?v=IXsA5Rpp25w
[4] Rocca, J. (2019, 9月23日). 理解变分自编码器(VAE). Towards Data Science. https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73
[5] Baidoo, F. A. (2015年8月28日). 傅里叶级数的一致收敛性研究 (暑期研究计划报告). 芝加哥大学 (https://math.uchicago.edu/~may/REU2015/REUPapers/Baidoo.pdf). 注:REU指“暑期研究计划”(Research Experience for Undergraduates)。

 随时随地看视频
随时随地看视频




