每个数据科学家都应该了解的线性代数概念-原创手记-慕课网

数据科学 你对线性代数足够熟悉吗？

线性代数是所有数据科学和机器学习任务的基础。

它是将理论模型转化为实际解决方案的语言。

它体现了允许算法从数据中学习的原则。

xkcd

它们被用来

数据表示：一种结构化的方式来组织和操作数据，允许将复杂的数据集表示为矩阵
降维：像PCA这样的技术依赖于线性代数来减少变量的数量，以提高模型效率而不丢失重要信息
优化：梯度下降，机器学习的核心引擎，使用线性代数来寻找函数的最小值
特征工程：线性变换和矩阵运算从现有数据中创建新的特征
相似度度量：嵌入以向量形式存储，并用于今天的推荐系统和AI聊天机器人
以及更多！

本文将探讨一些线性代数概念、视觉解释和代码示例。

让我们直接开始吧！

代码 → Deepnote Notebook

向量
∘ 单位向量
向量运算
∘ 向量加法
∘ 标量乘法
∘ 点积
向量空间
∘ 零空间（核）
∘ 生成
∘ 基
∘ 线性独立
矩阵
∘ 矩阵作为函数
∘ 线性变换
∘ 逆矩阵
∘ 奇异矩阵
∘ 单位矩阵。
∘ 对角矩阵
∘ 正交矩阵
∘ 矩阵乘法
∘ 迹
∘ 行列式
∘ 秩
∘ 特征向量和特征值

向量

图片由作者提供

这是线性代数的基本构建块。

有三种方式来思考向量。

第一个是从 物理视角 ：向量是空间中带有方向的箭头，由长度和方向定义。平面上的向量是二维的，而我们生活空间中的向量是三维的。

第二个是从 计算机科学的角度：向量是有序的数字列表。这个列表的长度决定了维度。

第三个是从 数学家的视角 ：向量可以是任何可以相加并且可以与数字相乘的对象。

单位向量

单位向量是模长为1的向量。它常被用来表示向量的方向，而不考虑其大小。

向量运算

向量加法

来源

两个向量按分量相加形成一个新的向量。

标量乘法

标量乘法是指将向量与标量（一个数）相乘，结果是方向与原向量相同（如果标量为负，则方向相反）且大小按标量的绝对值放大的向量。

点积

形式上，它是两个向量的欧几里得大小的乘积以及它们之间夹角的余弦值，反映了向量的长度及其方向关系。

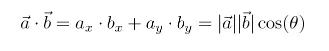
点积公式

直观地想象一下，这就像将一个向量的方向增长应用到另一个向量上，或者说“一个向量给另一个向量提供了多少推力或能量？”。结果是原始向量被增强了多少（正数、负数或零）。

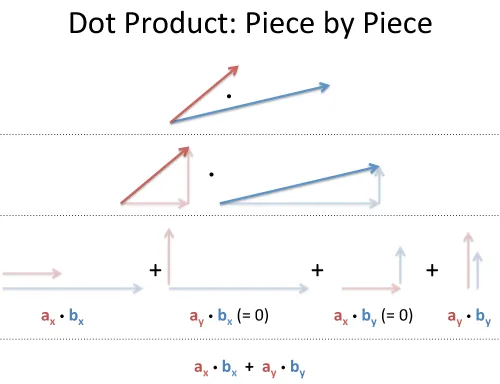
如果点积为0，它告诉我们这些向量是正交的。

来源

一个由 betterexplained 提供的有趣类比

想象红色向量是你当前的速度，蓝色向量是加速垫的方向。数字越大表示力量越大。点积就是你将获得的加速度。

使用公式，|a| 是你的初始速度，|b| 是最大加速值，你获得的加速百分比是 cos(𝛉)，总体加速效果为 |a| |b| cos(𝛉)

betterexplained

向量空间

一个向量（或线性）空间是由可以相加并可以与数字（在此上下文中称为标量）相乘（称为“标量乘法”）的向量集合组成。

为了将V称为向量空间，必须满足一系列公理。

来源

零空间（核）

零空间是一组向量，当这些向量与矩阵相乘时，结果为零向量。

它表示方程 Ax = 0 的解，其中 A 是给定的矩阵。

想象一个二维空间中有两个向量；矩阵的零空间可以被视为空间中的一个子空间，当这些向量与矩阵相乘时，会将它们压缩到原点（零向量）。

生成空间

给定一对向量 v 和 w ，你可以通过它们的线性组合到达的所有可能向量的集合。

ava + bw ，并且让 a 和 b 都是所有实数。

对于大多数向量对，它可以到达二维向量平面内的每一个点

3blue1brown 视频关于 span

当两个向量恰好在同一直线上时，它们仅限于通过原点的那条直线。

跨度的概念构成了基础概念的基础。

基底

基是一组线性独立的向量，这些向量可以张成整个向量空间。这意味着向量空间中的每一个向量都可以表示为基向量的线性组合。

可以将它们视为该空间中所有其他向量的构建块。

将单个向量视为箭头是有帮助的，但对于一组向量，可以将它们视为点。大多数基向量的组合可以覆盖整个二维空间的平面。

线性独立

一组向量是线性独立的，如果该组中的任一向量都不能表示为其他向量的线性组合（例如，x和y的线性组合可以表示为任何形如_ax + by_的表达式，其中a和b是常数）。

矩阵

矩阵是将输入和操作以行和列的形式组织的一种方式。

图片由作者提供

这里有一个2行2列的矩阵。

它们是一种数学工具，可以以结构化的方式解决问题。

矩阵作为函数

你可以把矩阵看作函数。就像一个Python函数接受输入参数，处理它们并返回输出一样，矩阵变换通过线性变换将输入向量转换为输出向量。

图片由作者提供

线性变换

来源

线性变换是在两个向量空间之间的一种映射 V → W，它保持向量加法和标量乘法的操作。

从实际意义上讲，将矩阵 A 应用于向量 x 以得到另一个向量 y （通过操作 Ax = y）是一种线性变换。

这在数据科学领域应用非常广泛：

维度缩减 : PCA 使用线性变换将高维数据映射到低维空间
数据变换 : 对数据集进行归一化或标准化是一种线性变换
特征工程 : 通过现有特征的组合创建新特征

下面是几种矩阵的形式

逆矩阵

一个矩阵与其逆矩阵相乘的结果是单位矩阵。

奇异矩阵

一个奇异矩阵是一个没有逆矩阵的方阵。这相当于说该矩阵的行列式为零或其秩小于其大小。

单位矩阵。

单位矩阵是一个方阵，其对角线上的值为1，其余位置均为0。在矩阵乘法中，它充当乘法单位元，通过乘以任何矩阵都不会改变该矩阵，就像数字1一样。

对角矩阵

对角矩阵是一种方阵，其中主对角线以外的所有元素都为零。它用于求解特征值，并用于计算行列式。

正交矩阵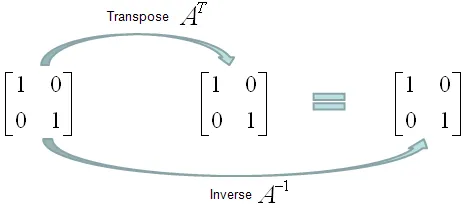

一个实数元素的方阵被认为是正交的，如果它的转置等于它的逆。

形式上，一个矩阵A是正交的，如果 A ᵀ A = A A ᵀ = I ，其中 I 是单位矩阵。

从几何角度看，一个矩阵是正交的，如果它的列和行都是正交单位向量，也就是说它们彼此垂直且长度为1。

回想一下，两个向量如果互相垂直（90度），它们的点积为0，那么这两个向量就是正交的。

矩阵乘法

你使用矩阵来进行矩阵乘法。

这里有一个来自线性代数直观指南的漂亮可视化。

来源

想象你正在将每个输入数据通过每个操作进行处理。

来源

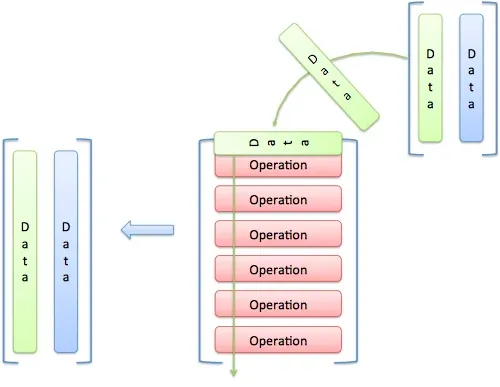
这里是一个这样的操作示例。

在进行操作后，你得到了这个。

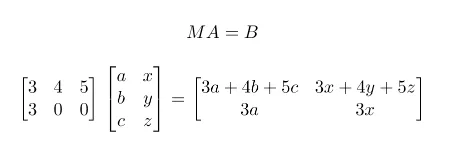
输入是一个 [3 x 2] 的矩阵，我们的操作矩阵是 [2 x 3]；结果是 [2 x 3] [3 x 2] = [2 x 2].

输入的大小必须与操作的大小匹配。

迹

矩阵的迹是其所有对角元素的和。它在基变换下保持不变，并提供了关于矩阵的重要信息，即迹是矩阵的所有特征值的和。

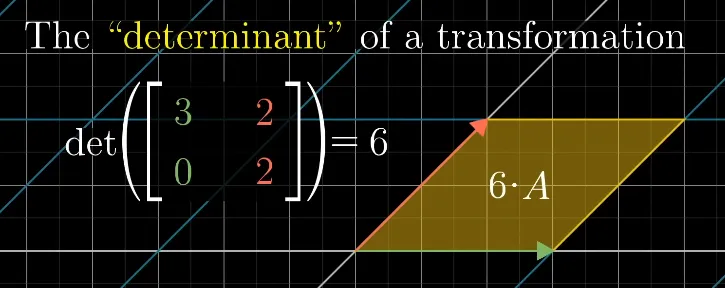
行列式

行列式是输出变换的大小。

如果输入是单位向量（面积或体积为1），那么行列式就是变换后的面积或体积的大小。

以这个矩阵为例。如果 A 的面积被缩放了 6 倍，那么这个变换的行列式就是 6。

来源

负的行列式告诉我们整个空间被翻转了。这种变换就像把一叠纸翻到另一面一样。

来源

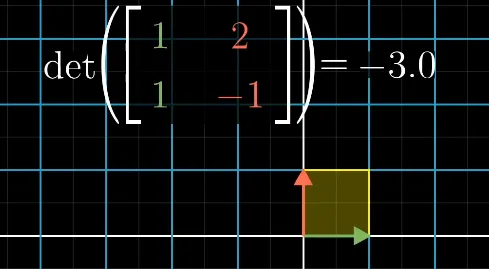
注意红色和绿色轴的方向被反转了。

行列式为0意味着矩阵是“破坏性的”，无法被逆转。类似于乘以0，信息会丢失。

行列式可以告诉我们一个矩阵是否可逆，如果 det(A) 为 0，那么逆矩阵不存在；该矩阵是奇异矩阵。

秩

矩阵中线性独立的列/行向量的最大数量。它表示由其行或列张成的向量空间的维度。

它也告诉我们在线性变换后的输出维度的数量。

当变换的输出是一条直线（即一维时），我们说该变换的秩为1。

如果所有的向量都落在某个二维平面上，我们就说这个变换的秩为2。

对于一个2x2矩阵，秩为2是其最好的状态，这被称为满秩。这意味着基向量可以遍历整个二维空间，并且行列式非零。

但对于 3x3 矩阵来说，秩为 2 表示它有所塌陷，但没有秩为 1 时那么严重。

特征向量和特征值

特征向量和特征值代表变换的“轴”。

特征向量在经过线性变换后方向不会改变。尽管方向不变，但大小可能会改变。这个大小，即特征向量被放大或缩小的程度，就是特征值。

想想当你旋转地球仪时；除了两极之外，每个地点都会朝向新的方向。而两极的方向不会改变。

这里是一个关于特征向量的视觉示例。

特征向量

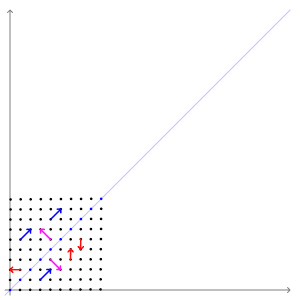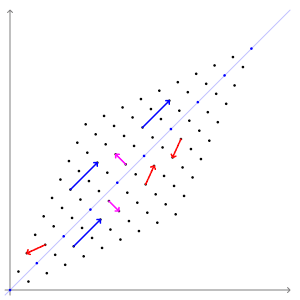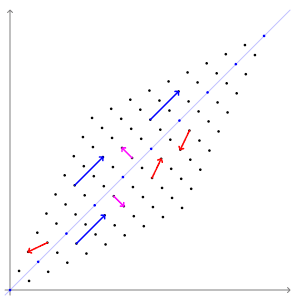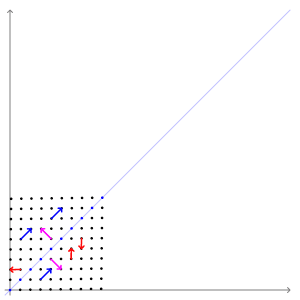
形式上，对于一个矩阵 A 和一个向量 v, 如果 Av = λv , 那么 λ 是一个特征值，而 v 是矩阵 A 的一个特征向量。

另一种说法是，方阵 A 的特征向量是那些满足 矩阵乘法 = 标量乘法 的向量。

阅读完毕！

资源

黑客攻击方法

可视化

Graphical Linear Algebra — 一种新的线性代数方法
3Blue1Brown的线性代数精华 — 精彩的动画，帮助可视化概念
inVectorize
直观数学

论文/课程/教材

保持连接！

务必关注bitgrit 数据科学出版物以保持更新！

想要与其他数据科学家讨论数据科学和人工智能的最新进展吗？加入我们的discord服务器!

跟随 Bitgrit 以了解工作坊和即将举行的竞赛的最新信息！