到本文结束时,你将能够构建自己的模型和机器学习库来做出预测。
让我们从编写一个简单的函数并讨论它开始:
def parabola_function(x):
return 3*x**2 - 4*x+5一个抛物线函数就是这样一个函数,当我们输入x坐标时,它会给出一组y坐标,我们可以将这些坐标映射成一条抛物线,例如,对于这一组x坐标。
x_point_list = np.arange(-5, 5, 0.25) # 从-5到5生成一个间隔为0.25的点列表
print(x_point_list)
----
[-5. -4.75 -4.5 -4.25 -4. -3.75 -3.5 -3.25 -3. -2.75 -2.5 -2.25
-2. -1.75 -1.5 -1.25 -1. -0.75 -0.5 -0.25 0. 0.25 0.5 0.75
1. 1.25 1.5 1.75 2. 2.25 2.5 2.75 3. 3.25 3.5 3.75]例如,如果我们给 parabolic_function 提供以下点,我们将得到:
x_point_list = np.arange(-5, 5, 0.25) # 从 -5 到 5 生成间隔为 0.25 的点列表
y_point_list = parabola_function(x_point_list)
print(y_point_list)
plt.plot(x_point_list,y_point_list) # 绘制我们的点
----
[100. 91.6875 83.75 76.1875 69. 62.1875 55.75 49.6875
44. 38.6875 33.75 29.1875 25. 21.1875 17.75 14.6875
12. 9.6875 7.75 6.1875 5. 4.1875 3.75 3.6875
4. 4.6875 5.75 7.1875 9. 11.1875 13.75 16.6875
20. 23.6875 27.75 32.1875 37. 42.1875 47.75 53.6875]最后,我们可以绘制这些点来可视化抛物线:
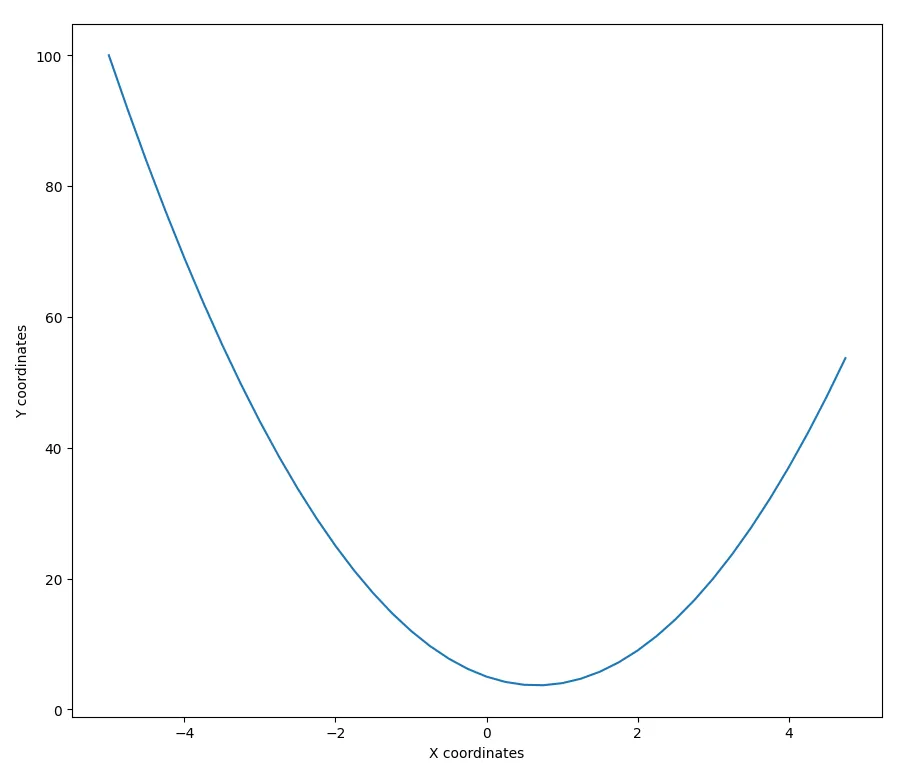
图片由作者提供。
现在,机器学习就派上用场了。具体来说,当我们想要找到上述曲线的最低点,即全局最小值时。从图上来看,这个点大概位于x轴0到2之间。
但是如果没有图表的话,我们如何确定这个点呢?
为了处理这个问题,我们引入了一个小小的“扰动”,让我们称之为 h:
h = 0.1
x = 3.0
parabola_function(x + h)
----
y = 21.430000000000007如上所示,通过将 h 添加到 x,我们可以开始探索函数的行为,并逐步向最小点靠近。我们可以在下面看到继续微调并尝试不同组合的情况:
h = 0.1
x = -4.4
parabola_function(x + h)
----
y = 77.67000000000002让我们自动化这个过程,我们的目标是使结果尽可能接近零。我们可以通过实际检查y的位置来实现这一点:推动后的新的y位置 —— 原来的y位置。另一种表示方法如下所示:
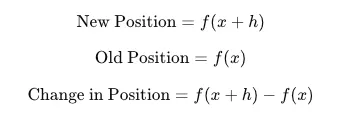
图片由作者提供。
为了自动化这个过程,我们在每次调整后计算新的 y 值和旧的 y 值之间的差值,然后除以 h 来得到步长。这有助于我们更接近最低点:
h = 0.0001
x = 2/3
(f(x+h) - f(x))/h
---
0.0002999999981767587通过重复这个过程,我们逐渐将 x 坐标靠近最小点,本例中的最小点大约是 x = 2/3。
另一种表示上述内容的方式是:
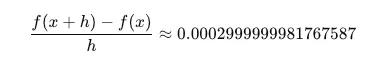
图片由作者提供。
最后我们找到了一个 x 和 h 的值,它们最能识别出最接近零的点:
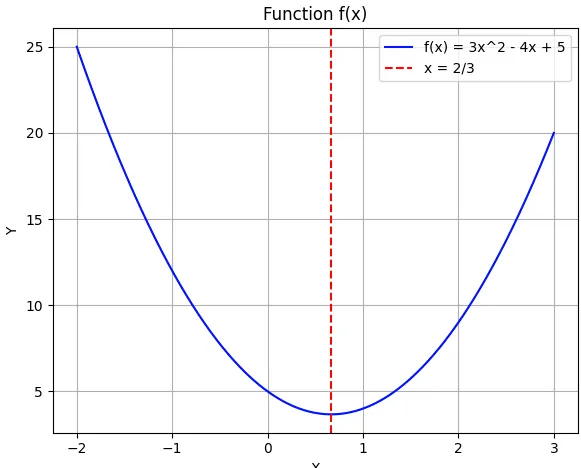
这种直觉在训练神经网络时是基础,其中算法会迭代地调整自身以最小化误差并做出更好的预测。
想想这个算法不仅仅是一个单一的数字,而是达到我们之前得到的最终状态的一系列数学运算的结果。
考虑到这一点,我们可以看到下面是如何得到 parabolic_function 的一个例子:
x = ML Framework(2.0) # 假设 x 是 2.0
y = 3 * x.times(x) # 表示 3x^2
y = y.minus(4 * x) # 表示 3x^2 - 4x
y = y.plus(5) # 表示 3x^2 - 4x + 5这里的神奇之处在于这些操作是如何自动化的。神经网络本质上是在大规模地执行这些计算,通过调整和优化自身(权重和偏置)来最小化误差并提高预测的准确性。
但是神经网络是如何计算和更新这些值的呢?关键在于我们如何表示和执行数学运算。例如,我们可以假设 x 是我们的原始输入,w 是我们赋予 x 的权重,而 b 是我们的偏置(或微调):
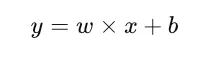
图片由作者提供。
接下来更明显的问题是:我们如何更新这些值?为此,我们需要评估我们的预测值(网络的输出)与实际值(目标输出)的接近程度。
我们通过使用当前的值进行假设预测,然后计算这个预测值与实际目标值之间的差异来实现这一点。这个差异被称为“损失”,它让我们了解我们的预测与实际值相差多少。
为了改进并解决损失差异的问题,我们需要从后向前遍历网络,并评估损失相对于每个权重的变化。这里我们可以引入深度优先搜索(DFS)的概念,以便更深入地理解我们将要进行的操作。
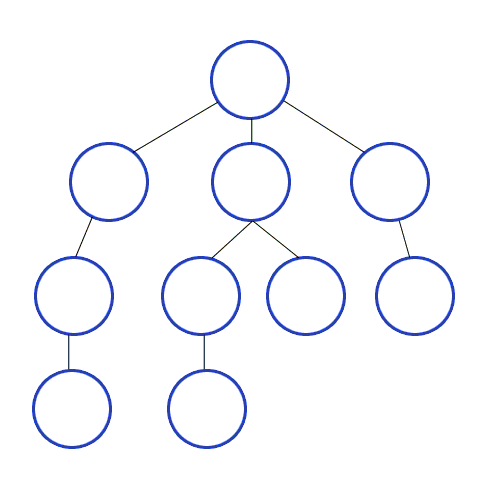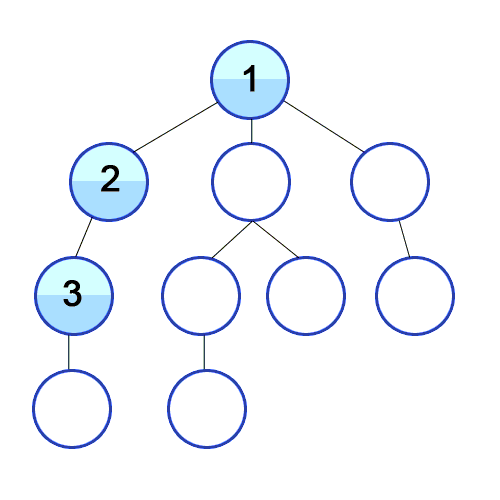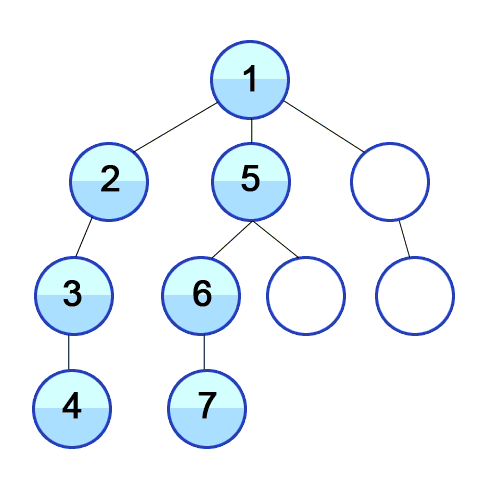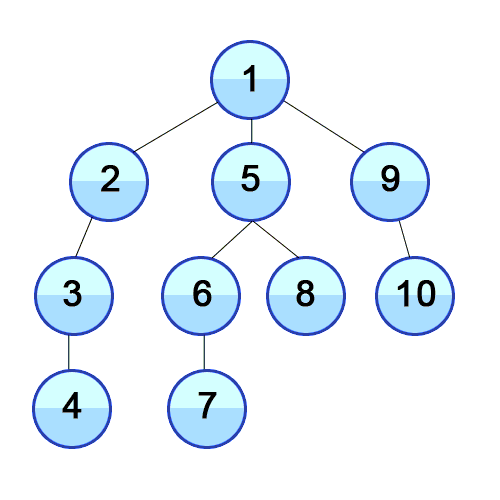
来源:Wiki Create Commons (链接 — Depth-First-Search.gif?20090326120256)
DFS 是一种递归探索算法,可以帮助我们理解神经网络中反向传播的过程。反向传播是通过逆序遍历网络来计算我们的值,确保每个数学运算都能正确完成。
我们通过“自底向上”的方式组织我们的值,类似于反向传播,本质上是在做同样的事情。这种方法被称为有向无环图(DAG)的拓扑排序。
它确保网络中的每个值都按照深度优先的顺序访问,这意味着我们在回溯之前尽可能沿着一条路径深入探索。
总体思路是我们不断调整值,最终使我们的假设预测与实际预测相匹配或接近匹配。一旦完成这一步,我们就可以有效地解决预测问题。以下是我们将要进行的概述:

图片由作者提供。
这段代码与上面的图相比会显得非常简单:
def backward(self):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(self)
self.grad = 1.0
for node in reversed(topo):
node._backward()这段代码就是我们实现反向传播所需的一切,反向传播将是设计的关键部分。现在,让我们来看一下这个概念的一个实际应用。
预测房价假设我们有一些数据,即一套一居室的房子售价为100,000美元,一套两居室的房子售价为200,000美元,一套三居室的房子售价为300,000美元。现在,我们想利用这些数据来进行预测。
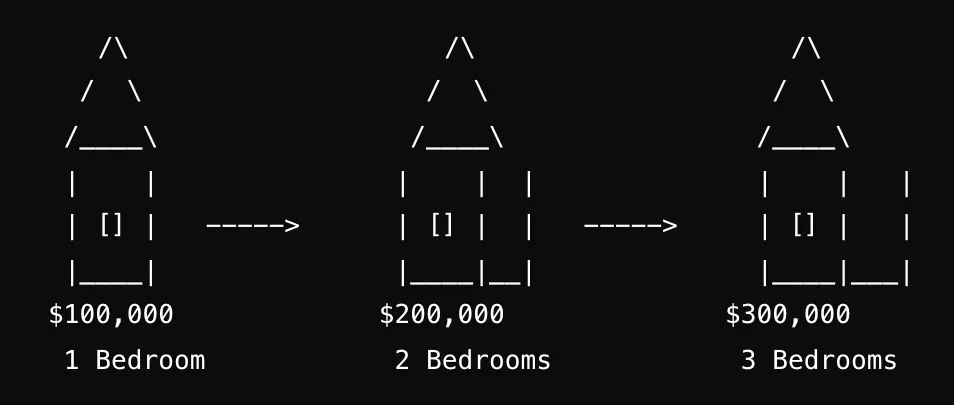
图片由作者提供。
通常,机器学习意味着我们的计算机程序或软件在没有被明确编程的情况下就能做出预测并提供输出。换句话说,我们不会编写直接计算结果的代码——相反,程序从我们提供的数据中学习,然后基于这些学习进行预测。首先,让我们先对现有的数据进行归一化和预处理。
卧室数 价格 归一化后的价格
1卧室 -----> $100,000 -----> 1.0
2卧室 -----> $200,000 -----> 2.0
3卧室 -----> $300,000 -----> 3.0现在,假设我们想用神经网络来预测一套5卧室房子的价格。目标是让神经网络从现有的数据(1卧室、2卧室和3卧室的价格)中学习,并利用这些学习结果来预测更多卧室的房子的价格。
预测价格 = 模型(卧室_5)
---
500,000所以,我们首先需要做的是创建我们的机器学习框架。可以将其视为构建一个类似于TensorFlow、PyTorch或JAX的流行库的简化版本。让我们分解一下我们需要的一些关键组件:
- value : 这基本上是我们之前讨论的内容。它是由我们的预测对损失的贡献程度所决定的梯度。
- backward : 这里存储我们实际的反向传播函数,用于将错误反向传播并通过网络更新权重。
- data : 这些是我们实际处理的值,比如房价。
- prev : 这用于跟踪我们是否已经访问过某个节点。
class ML_Framework:
def __init__(self, data, _children=()):
self.data = data
self.value = 0.0
self._backward = lambda: None
self._prev = set(_children)在这个类中,data 存储实际的数据点(如房屋价格),value 初始值为零,表示梯度,该梯度将在模型学习过程中被更新,_backward 初始设置为一个占位函数,但将会被更新为执行实际的反向传播操作,而 _prev 用于跟踪我们已经访问过的节点。
一旦我们有了框架,下一步就是定义我们的模型是什么样的。在这个例子中,我们将使用一个单层感知器。这里我不深入细节,但关键点是我们将声明我们的偏置并设置一些初始权重。
class SingleLayerNeuron:
def __init__(self, num_of_inputs):
self.weights = [ML_Framework(0.09) for _ in range(num_of_inputs)]
self.bias = ML_Framework(-0.9)
def weights_bias_parameters(self):
return self.weights + [self.bias]
def zero_value(self):
for p in self.weights_bias_parameters():
p.value = 0.0
def __call__(self, x):
cumulative_sum = self.bias
for wi, xi in zip(self.weights, x):
product = wi.times(xi)
cumulative_sum = cumulative_sum.plus(product)
return cumulative_sum我们现在可以训练我们的模型:
model = SingleLayerNeuron(1)
print("初始权重:", [w.data for w in model.weights])
print("初始偏置:", model.bias.data)
learning_rate = 0.05
epochs = 100
for epoch in range(epochs):
total_loss = 0
for i in range(num_of_model_inputs):
x_model_input = x_input_values[i]
y_desired_output = y_output_values[i]
model_prediction = model(x_model_input)
loss = squared_error_loss(model_prediction, y_desired_output)
model.zero_value()
loss.backward()
total_loss = total_loss + loss.data
for weights_bias_parameters in model.weights_bias_parameters():
weights_bias_parameters.data = weights_bias_parameters.data - (learning_rate * weights_bias_parameters.value)
mean_squared_error = total_loss / num_of_model_inputs
if epoch % 1 == 0:
print(f"Epoch {epoch}, Loss: {mean_squared_error}")
----------------
输出:
初始权重: [0.09]
初始偏置: -0.9
Epoch 0, Loss: 3.2761
Epoch 1, Loss: 2.096704
Epoch 2, Loss: 1.3418905599999997
Epoch 3, Loss: 0.8588099583999995
Epoch 4, Loss: 0.5496383733759997
Epoch 5, Loss: 0.35176855896063985
Epoch 6, Loss: 0.2251318777348095
Epoch 7, Loss: 0.14408440175027803
Epoch 8, Loss: 0.09221401712017797
Epoch 9, Loss: 0.05901697095691388
Epoch 10, Loss: 0.03777086141242487
Epoch 11, Loss: 0.02417335130395193
Epoch 12, Loss: 0.015470944834529213
Epoch 13, Loss: 0.009901404694098687
Epoch 14, Loss: 0.006336899004223174
Epoch 15, Loss: 0.004055615362702837
Epoch 16, Loss: 0.0025955938321298136
Epoch 17, Loss: 0.0016611800525630788
Epoch 18, Loss: 0.0010631552336403704
Epoch 19, Loss: 0.0006804193495298324
Epoch 20, Loss: 0.0004354683836990928
Epoch 21, Loss: 0.0002786997655674194
Epoch 22, Loss: 0.00017836784996314722
Epoch 23, Loss: 0.00011415542397641612
Epoch 24, Loss: 7.305947134490555e-05
Epoch 25, Loss: 4.675806166074016e-05
Epoch 26, Loss: 2.9925159462873704e-05
Epoch 27, Loss: 1.915210205623956e-05
Epoch 28, Loss: 1.2257345315993629e-05
Epoch 29, Loss: 7.844701002235673e-06
Epoch 30, Loss: 5.020608641430632e-06这种损失的逐渐减少展示了我们的模型预测的准确性是如何随着它继续根据输入数据调整权重和偏置而提高的。最终,训练完成后,我们可以使用训练好的模型来预测一个5卧室房子的价格:
bedroom_5 = [ML_Framework(5)]
predicted_price = model(bedroom_5)
predicted_price_denormalized = predicted_price.data * 100000
print(f"预测的5卧室房子的价格: ${predicted_price_denormalized:.2f}")
-------
预测的5卧室房子的价格: $498000.00如你所见,预测的价格与我们预期的非常接近,尽管并非完美。通过更先进的模型和技术,预测的准确性和适用性可以得到显著提升。但基本原则保持不变,即通过迭代训练过程,神经网络学会了预测的内容,并随着时间的推移和调整而不断改进。
分解
让我们稍微拆解一下过程,以便那些对技术细节感兴趣的人更好地理解。在Epoch 0,weight初始化为0.09,而bias设置为-0.9。在第一个训练周期中,模型进行预测。这个预测是通过将卧室的数量(在这个例子中是1)乘以weight(0.09),然后加上bias(-0.9)计算得出的。这个公式可以表示为:

图片由作者提供。
期望的输出——模型理想情况下应该预测的价格——是 100,000,这对应于一间卧室的房子的实际价格。然而,假设模型预测的价格是 80,000。这个预测与目标价格 100,000 相差甚远。
为了提高预测的准确性,神经网络会根据误差调整其 weights 和 bias。确定如何进行这些调整的过程称为 backpropagation。
在 反向传播 过程中,模型计算如果稍微调整 权重 和 偏置,损失(预测价格与实际价格之间的误差)会如何变化。这里就用到了我们之前讨论过的 梯度,也就是“值”。
学习率 在这个例子中设置为 0.04,控制调整的大小。模型使用这个 学习率 来确保不会做出过大的调整,这可能会使学习过程变得不稳定。
模型通过减去计算出的gradient来更新weights和bias,这有助于它在后续的周期中做出更准确的预测。通过在多个周期中重复这个过程,神经网络逐渐提高了预测房价的准确性。
致谢及进一步阅读
本文讨论的模型代码可以在这里找到: https://github.com/seanjudelyons/Single_Layer_Perceptron。这个示例使用了DFS算法作为深入链式法则的替代方案,并且大致基于单层感知器的概念。
对于对此处想法感兴趣的人,你们可能想要探索Rumelhart、Hinton和Williams(1986)的“通过反向传播错误来学习表示”。另外,也可以看看Frank Rosenblatt的“感知器”(1957),这是一篇有趣的读物。
本文很大程度上受到了Andrej Karpathy、Andrew Ng和Laurence Moroney在机器学习领域的教育努力的启发;我建议大家可以去了解他们。他们对领域的贡献在于使复杂概念对全球学习者易于理解,这一点非常宝贵。
下面是当我第一次遇到神经网络成本函数时的屏幕截图。我们已经走了很长一段路,使得这样的复杂概念能够被全世界的学习者理解。

图片由作者提供。

 随时随地看视频
随时随地看视频




