课程内容
二叉树 Binary Tree
- 对于大量的输入数据,链表的线性访问时间 太慢,不宜使用
- 树结构本身是一种天然的组织结构
- 将数据使用树结构存储后,出奇的高效
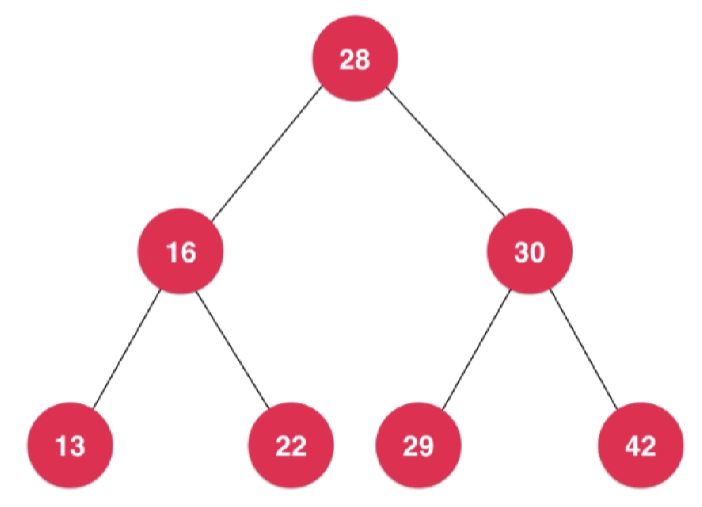
- 和链表一样,动态数据结构
- 二叉树具有唯一根节点
- 二叉树每个节点最多有两个孩子,一个孩子都没有的节点通常称为叶子节点
- 二叉树每个节点最多只有一个父亲节点,整个二叉树中只有一个节点是没有父亲节点的,就是根节点
class Node {
E e;
Node left;//左孩子
Node right;//右孩子
}
链表也具有天然的递归结构,但由于链表是线性的,所以对于链表相关的操作,使用循环的方式完全可以处理;但对于树来说,使用递归的写法要比非递归的写法要简单很多的
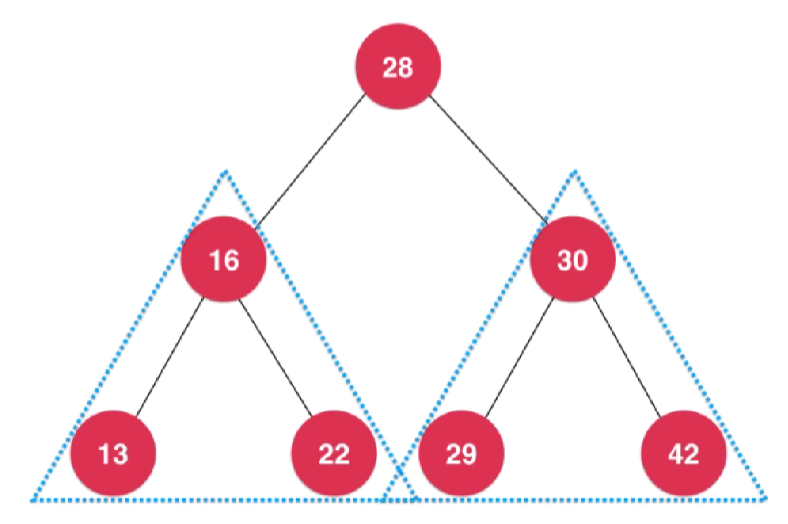
- 每个节点的左子树也是二叉树
- 每个节点的右子树也是二叉树
每一棵二叉树它的左侧和右侧又分别连接了两颗二叉树,这两颗二叉树都是节点个数更小的两颗二叉树。
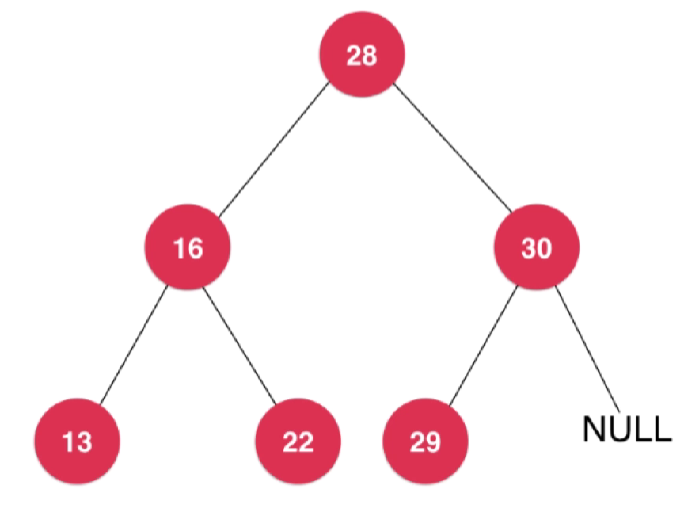
- 二叉树不一定是满二叉树,满二叉树是指除了叶子节点之外,都有两个孩子
- 一个节点也可以二叉树,只有一个节点也可以是链表
- null 空也可以是二叉树,空节点也可以是链表
二分搜索树 Binary Search Tree
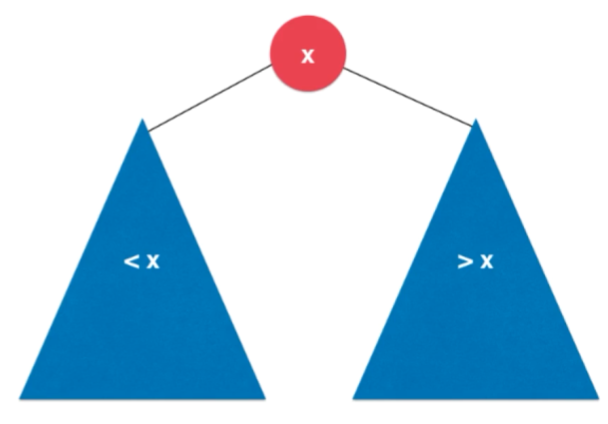
- 二分搜索树是二叉树
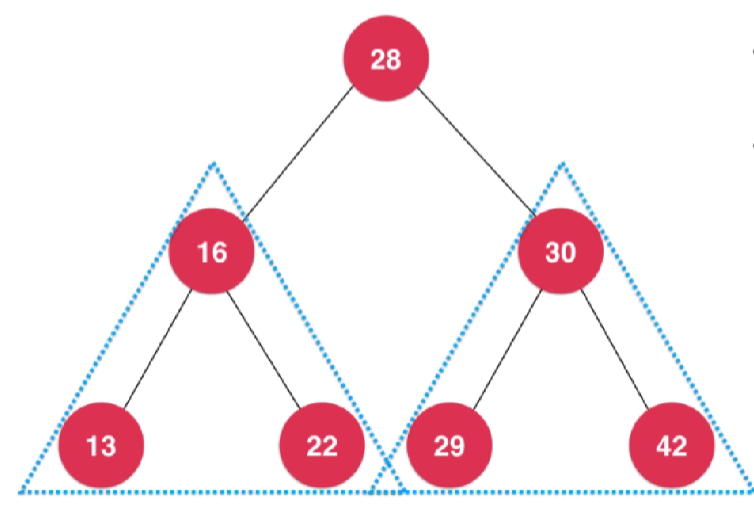
- 二分搜索树每个节点的值:
- 大于其左子树的所有节点的值
- 小于其右子树所有节点的值
- 存储的元素必须具有可比较性 (如果要加快搜索的话,就必须对数据有一定的要求)
本二分搜索树不包含重复元素,如果想包含重复元素的话,有两种实现方式
- 定义左子树小于等于节点;或者右子树大于等于节点
- 定义节点的count > 注意:数组和链表,可以有重复元素
- 遍历操作就是把所有的节点都访问一遍
- 访问的原因和业务相关
- 在线性结构性下,遍历是极其容易的

- 从根节点开始看,是不是查找的元素。如果小于根节点就在左子树中继续进行这个操作,如果大于根节点,就在右子树中继续进行操作
- 对于遍历操作,两棵子树都要顾及
- 访问节点的时机放在了访问左子树和右子树的前面
- 访问节点的时机放在了访问左子树和右子树的中间
- 二分搜索树的中序遍历结果是顺序的,正因为这种性质,二分搜索树也称为排序树
- 访问节点的时机放在了访问左子树和右子树的后面
- 应用场景:必须处理完节点的孩子节点之后再来处理这个节点,比如 为二分搜索树释放内存(Java语言有GC,所以用不到)
- 对于每一个节点都连接着左子树和右子树,在具体遍历的时候,每一个节点都有三次的访问机会,遍历完左子树之后会回到该节点;然后继续去遍历右子树,遍历完右子树后会继续回到该节点。
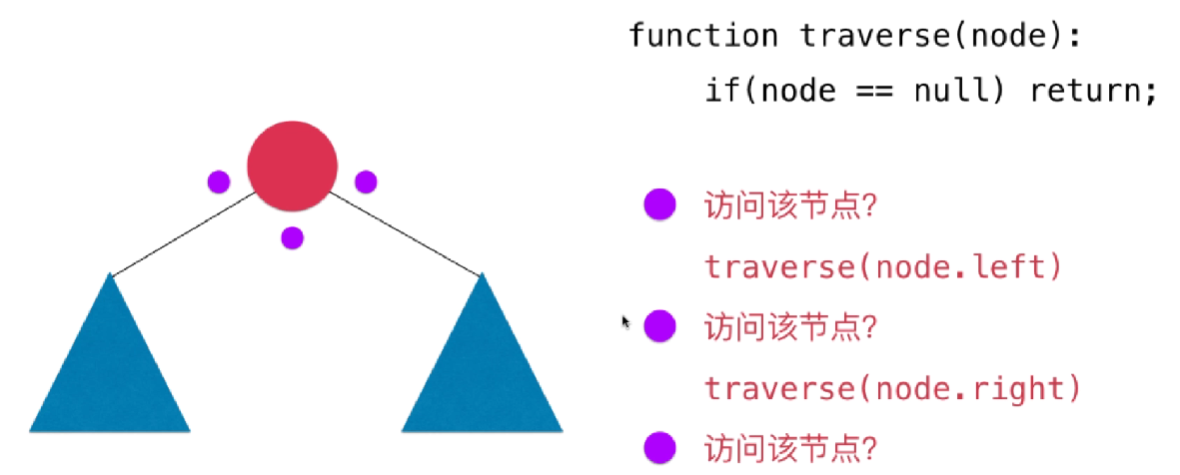
- 二分搜索树的前中后遍历其实就对应着每个节点的三个紫色的点,在哪里进行真正的访问操作
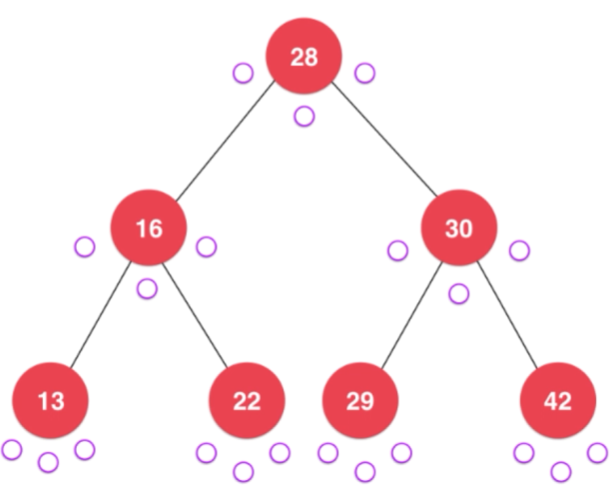
- 前序遍历就是在第一次访问节点的时候访问节点值
- 中序遍历就是在第二次访问节点的时候访问节点值
- 中序遍历就是在第三次访问节点的时候访问节点值
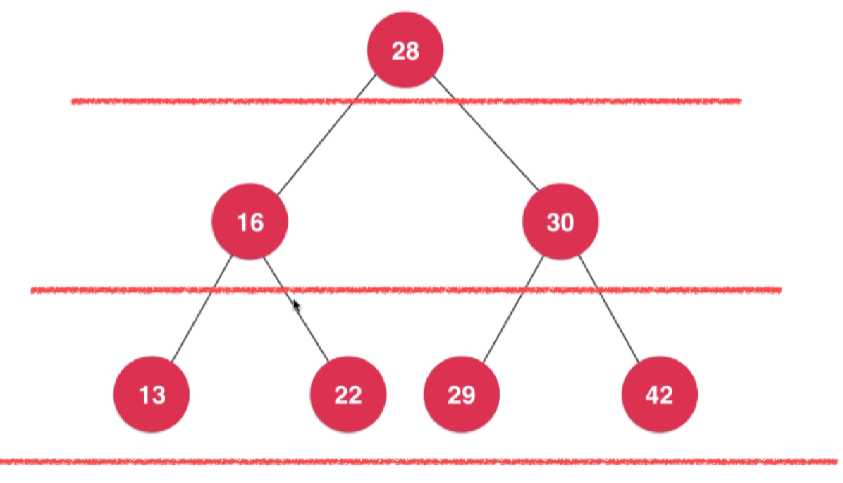
- 二分搜索树的前序、中序、后序遍历其实上都是深度优先的遍历。
- 根节点为深度为0的节点,一层一层的进行遍历
- 需要借助队列这种数据结构,从根节点开始,排队进入队列,队列中存储的就是待遍历的元素;每次遍历一个元素之后,将它的左右孩子也进行入队操作
- 广度优先遍历的意义:主要用于搜索策略上,而不是用于遍历操作上(对于遍历来说,深度优先遍历和广度优先遍历是没有区别的),常用于算法设计中-最短路径
- 找到二分搜索树中的最大值和最小值
1962年,Hibbard提出-Hibbard Deletion
-
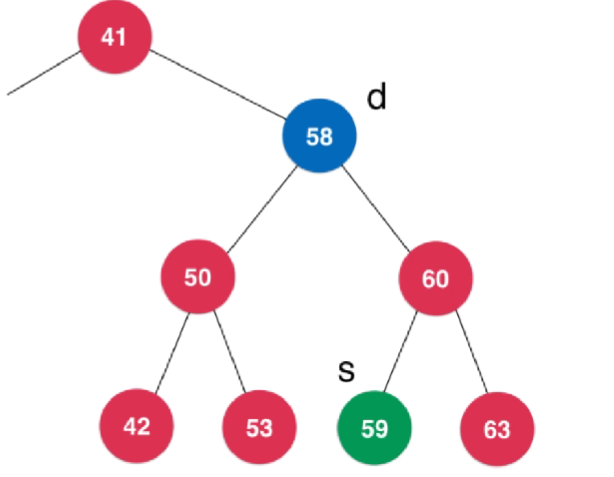
删除左右都有孩子的节点,取比要删除节点要大的最小元素节点代替被删除节点,即找要删除元素的后继
-
需要找到对于要删除元素d的右子树来说相应的最小值的点,我们称这个点为s,s是d的后继
-
s->right=delMin(d->right);
-
s->left=d->left
-
删除d,s是新的子树的根节点
-
也可以通过找d的前去p来取代d,无论是使用前驱还是后继,都能继续保持二分搜索树的性质
- 二分搜索树具有顺序性,放在二分搜索树中的所有元素都是有序的(中序遍历得到的结果就是有序的),可以非常轻易地得到最大值 minimum 和最小值 maximum,包括给定一个值拿到它的前驱 successor 和后继 predecessor,
- floor,ceil ,比如寻找45的floor和ceil,floor是比45小的最大的元素,ceil是比45大的最小的元素
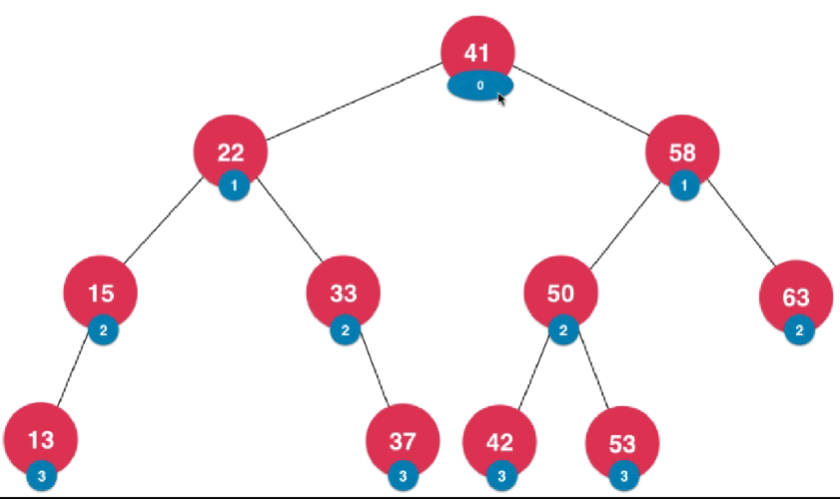
- rank,select,rank是查看元素排名第几 rank 58 求58是排名第几的元素;select是一个反向的操作,排名是第10名的元素是谁;实现rank和select最好的方式是每一个节点同时维护一个size,size表示以这个节点为根的二分搜索树有多少个元素,有了这个size之后就可以移除整体size 了
- 维护depth的二分搜索树
- 支持重复元素的二分搜索树;1. 定义左子树或右子树等于父节点即可;2.在Node作用域中定义count,记录重复元素,–后等于0,才彻底删除元素
学习收获
今天学习了经典树结构中的二叉树和二分搜索树。收获巨大。

 随时随地看视频
随时随地看视频




