学习课程:算法与数据结构高手养成-求职提升特训课
章节名称:第5章 动态规划基础 Dynamic Programming Basics
讲师:吉他熊
课程内容:
DP之所以快:每个重叠子问题,只计算一次
DP的两种模型:记忆化搜索,递推+枚举
如何找出重叠子问题
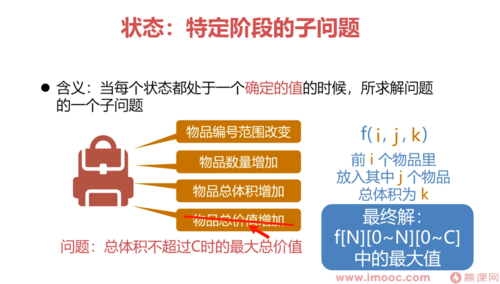
明确目标状态(能够构成解的状态)
定义子问题(从当前状态到目标状态的最优代价)
确认子问题的重复性
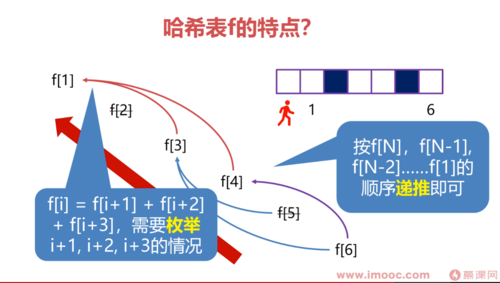
递推的优缺点
优点:只需要循环,不用担心栈溢出
缺点:不够直观(如何确定子问题求解顺序,如何确定一个子问题与其他哪些子问题相关)
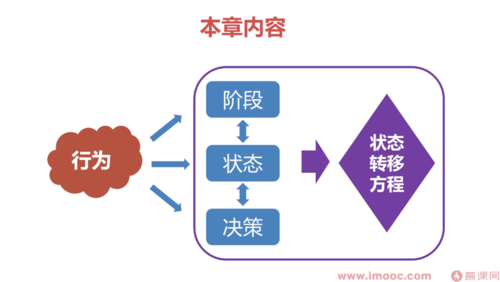
DP三要素:阶段、状态、决策
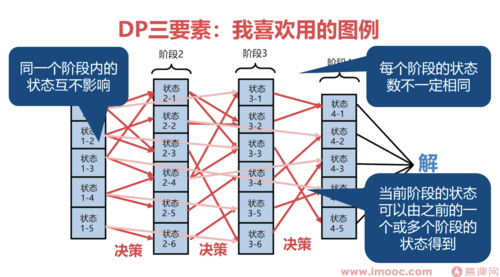
DP的核心:行为
三要素并不是割裂的,是有机统一的
将三要素联系起来的单一要素:行为
行为产生变化,变化了才有问题,才需要求解
行为的三种常见类别
取舍:给出若干个选项,选择其中一个或多个,加入当前方案,或从当前方案去掉
移动:自身属性不变,相对时空位置发生改变
更改:更改自身属性


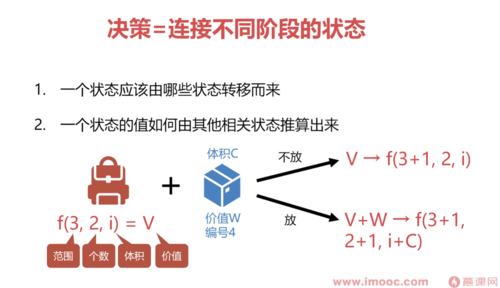
决策的注意事项
决策的变化范围不能超出阶段的限制范围
一部分状态的值无法考决策计算,而是作为初始状态,需要考初始化给他们赋值
重叠子问题是“DP效率更高的原因”,而不是“DP能得到正确结果的原因”
最优子结构+无后效性=DP能得到正确结果
最优子结构+无后效性+重叠子问题=DP能高效地得到正确结果
最优子结构
一个问题的最优解,一定由它的子问题的最优解得来
判断最优子结构
不具备最优子结构——子问题无法判断最优/存在反例
判断无后效性
唯一准则:状态之间没有循环依赖
学习收获:
DP问题很多阶段可以省略,但在分析问题的时候,这些阶段的过程不可以省掉,“学会走路前,不要急着跑”;否则很难理解或者很难去分析并解决下一个类似的DP问题
不要在分析的时候图省事,随便省略阶段,否则可能会将问题错判为不具有最优子结构
要注意区分状态定义具有后效性与问题本身具有无后效性;状态定义的后效性可以通过增加新的阶段来消除依赖;增加新的阶段意味着重叠子问题的减少,从而降低DP效率
打卡截图:

 随时随地看视频
随时随地看视频




