韩明聪,TiDB Contributor,上海交通大学 IPADS 实验室博士研究生,研究方向为系统软件。本文主要介绍了如何在 TiDB 中使用纯 SQL 训练一个机器学习模型。
前言
众所周知,TiDB 5.1 版本增加了很多新特性,其中有一个特性,即 ANSI SQL 99 标准中的 Common Table Expression (CTE)。一般来说,CTE 可以被用作一个 Statement 作用于临时的 View,将一个复杂的 SQL 解耦,提高开发效率。但是,CTE 还有一个重要的使用方式,即 Recursive CTE,允许 CTE 引用自身,这是完善 SQL 功能的最后一块核心的拼图。在 StackOverflow 中有过这样一个讨论 “Is SQL or even TSQL Turing Complete”,其中点赞最多的回复中提到这样一句话:
“ In this set of slides Andrew Gierth proves that with CTE and Windowing SQL is Turing Complete, by constructing a cyclic tag system, which has been proved to be Turing Complete. The CTE feature is the important part however – it allows you to create named sub-expressions that can refer to themselves, and thereby recursively solve problems.”
Iris Dataset
首先要选择一个简单的机器学习模型和任务,我们先尝试 sklearn 中的入门数据集 iris dataset。这个数据集共包含 3 类 150 条记录,每类各 50 个数据,每条记录都有 4 项特征:花萼长度、花萼宽度、花瓣长度、花瓣宽度,可以通过这 4 个特征预测鸢尾花卉属于 iris-setosa,iris-versicolour,iris-virginica 中的哪一品种。
当下载好数据后(已经是 CSV 格式),我们先将数据导入到 TiDB 中。
mysql> create table iris(sl float, sw float, pl float, pw float, type varchar(16));
mysql> LOAD DATA LOCAL INFILE 'iris.csv' INTO TABLE iris FIELDS TERMINATED BY ',' LINES TERMINATED BY '\n' ;
mysql> select * from iris limit 10;+------+------+------+------+-------------+| sl | sw | pl | pw | type |+------+------+------+------+-------------+| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa || 4.9 | 3 | 1.4 | 0.2 | Iris-setosa || 4.7 | 3.2 | 1.3 | 0.2 | Iris-setosa || 4.6 | 3.1 | 1.5 | 0.2 | Iris-setosa || 5 | 3.6 | 1.4 | 0.2 | Iris-setosa || 5.4 | 3.9 | 1.7 | 0.4 | Iris-setosa || 4.6 | 3.4 | 1.4 | 0.3 | Iris-setosa || 5 | 3.4 | 1.5 | 0.2 | Iris-setosa || 4.4 | 2.9 | 1.4 | 0.2 | Iris-setosa || 4.9 | 3.1 | 1.5 | 0.1 | Iris-setosa |+------+------+------+------+-------------+10 rows in set (0.00 sec)
mysql> select type, count(*) from iris group by type;+-----------------+----------+| type | count(*) |+-----------------+----------+| Iris-versicolor | 50 || Iris-setosa | 50 || Iris-virginica | 50 |+-----------------+----------+3 rows in set (0.00 sec)
Softmax Logistic Regression
这里我们选择一个简单的机器学习模型 —— Softmax 逻辑回归,来实现多分类。(以下的图与介绍均来自百度百科)
在 Softmax 回归中将 x 分类为类别 y 的概率为: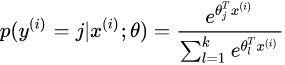
代价函数为:

可以求得梯度:

因此可以通过梯度下降方法,每次更新梯度:
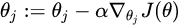
Model Inference
我们先写一个 SQL 来实现 Inference,根据上面定义的模型和数据,输入的数据 X 共有五维(sl, sw, pl, pw 以及一个常数 1.0),输出使用 one-hot 编码。mysql> create table data( x0 decimal(35, 30), x1 decimal(35, 30), x2 decimal(35, 30), x3 decimal(35, 30), x4 decimal(35, 30), y0 decimal(35, 30), y1 decimal(35, 30), y2 decimal(35, 30));
参数共有 3 类 * 5 维 = 15 个:mysql>insert into dataselect sl, sw, pl, pw, 1.0, case when type='Iris-setosa'then 1 else 0 end, case when type='Iris-versicolor'then 1 else 0 end, case when type='Iris-virginica'then 1 else 0 endfrom iris;
先全部初始化为 0.1,0.2,0.3(这里选择不同的数字是为了方便演示,也可以全部初始化为0.1):mysql> create table weight( w00 decimal(35, 30), w01 decimal(35, 30), w02 decimal(35, 30), w03 decimal(35, 30), w04 decimal(35, 30), w10 decimal(35, 30), w11 decimal(35, 30), w12 decimal(35, 30), w13 decimal(35, 30), w14 decimal(35, 30), w20 decimal(35, 30), w21 decimal(35, 30), w22 decimal(35, 30), w23 decimal(35, 30), w24 decimal(35, 30));
mysql> insert into weight values ( 0.1, 0.1, 0.1, 0.1, 0.1, 0.2, 0.2, 0.2, 0.2, 0.2, 0.3, 0.3, 0.3, 0.3, 0.3);
下面我们写一个 SQL 来统计对所有的 Data 进行 Inference 后结果的准确率。
为了方便理解,我们先给一个伪代码描述这个过程:
weight = ( w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24)for data(x0, x1, x2, x3, x4, y0, y1, y2) in all Data: exp0 = exp(x0 * w00, x1 * w01, x2 * w02, x3 * w03, x4 * w04) exp1 = exp(x0 * w10, x1 * w11, x2 * w12, x3 * w13, x4 * w14) exp2 = exp(x0 * w20, x1 * w21, x2 * w22, x3 * w23, x4 * w24) sum_exp = exp0 + exp1 + exp2 // softmax p0 = exp0 sum_exp p1 = exp1 sum_exp p2 = exp2 sum_exp // inference result r0 = p0 > p1 and p0 > p2 r1 = p1 > p0 and p1 > p2 r2 = p2 > p0 and p2 > p1 data.correct = (y0 == r0 and y1 == r1 and y2 == r2)return sum(Data.correct) count(Data)
在上述代码中,我们对 Data 中的每一行元素进行计算,首先求三个向量点乘的 exp,然后求 softmax,最后选择 p0, p1, p2 中最大的为 1,其余为 0,这样就完成了一个样本的 Inference。如果一个样本最后 Inference 的结果与它本来的分类一致,那就是一次正确的预测,最后我们对所有样本中正确的数量求和,即可得到最后的正确率。
下面给出 SQL 的实现,我们选择把 data 中的每一行数据都和 weight (只有一行数据) join 起来,然后计算每一行数据的 Inference 结果,再对正确的样本数量求和:
可以看到上述 SQL 几乎是按步骤实现了上述伪代码的计算过程,得到结果:select sum(y0 = r0 and y1 = r1 and y2 = r2) count(*)from (select y0, y1, y2, p0 > p1 and p0 > p2 as r0, p1 > p0 and p1 > p2 as r1, p2 > p0 and p2 > p1 as r2 from (select y0, y1, y2, e0/(e0+e1+e2) as p0, e1/(e0+e1+e2) as p1, e2/(e0+e1+e2) as p2 from (select y0, y1, y2, exp( w00 * x0 + w01 * x1 + w02 * x2 + w03 * x3 + w04 * x4 ) as e0, exp( w10 * x0 + w11 * x1 + w12 * x2 + w13 * x3 + w14 * x4 ) as e1, exp( w20 * x0 + w21 * x1 + w22 * x2 + w23 * x3 + w24 * x4 ) as e2 from data, weight) t1 )t2 )t3;
下面我们就对模型的参数进行学习。+-----------------------------------------------+| sum(y0 = r0 and y1 = r1 and y2 = r2)/count(*) |+-----------------------------------------------+| 0.3333 |+-----------------------------------------------+1 row in set (0.01 sec)
Model Training
Notice:这里为了简化问题,不考虑 “训练集”、“验证集” 等问题,只使用全部的数据进行训练。
我们还是先给出一个伪代码,然后根据伪代码写出一个 SQL:
weight = ( w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24)for iter in iterations: sum00 = 0 sum01 = 0 ... sum23 = 0 sum24 = 0 for data(x0, x1, x2, x3, x4, y0, y1, y2) in all Data: exp0 = exp(x0 * w00, x1 * w01, x2 * w02, x3 * w03, x4 * w04) exp1 = exp(x0 * w10, x1 * w11, x2 * w12, x3 * w13, x4 * w14) exp2 = exp(x0 * w20, x1 * w21, x2 * w22, x3 * w23, x4 * w24) sum_exp = exp0 + exp1 + exp2 // softmax p0 = y0 - exp0 sum_exp p1 = y1 - exp1 sum_exp p2 = y2 - exp2 sum_exp sum00 += p0 * x0 sum01 += p0 * x1 sum02 += p0 * x2 ... sum23 += p2 * x3 sum24 += p2 * x4 w00 = w00 + learning_rate * sum00 Data.size w01 = w01 + learning_rate * sum01 Data.size ... w23 = w23 + learning_rate * sum23 Data.size w24 = w24 + learning_rate * sum24 Data.size
看上去比较繁琐,因为我们这里选择把 sum, w 等向量给手动展开。
设置学习率和样本数量
迭代一次:mysql> set @lr = 0.1;Query OK, 0 rows affected (0.00 sec)mysql> set @dsize = 150;Query OK, 0 rows affected (0.00 sec)
得到的结果是一次迭代后的模型参数:select w00 + @lr * sum(d00) @dsize as w00, w01 + @lr * sum(d01) @dsize as w01, w02 + @lr * sum(d02) @dsize as w02, w03 + @lr * sum(d03) @dsize as w03, w04 + @lr * sum(d04) @dsize as w04 , w10 + @lr * sum(d10) @dsize as w10, w11 + @lr * sum(d11) @dsize as w11, w12 + @lr * sum(d12) @dsize as w12, w13 + @lr * sum(d13) @dsize as w13, w14 + @lr * sum(d14) @dsize as w14, w20 + @lr * sum(d20) @dsize as w20, w21 + @lr * sum(d21) @dsize as w21, w22 + @lr * sum(d22) @dsize as w22, w23 + @lr * sum(d23) @dsize as w23, w24 + @lr * sum(d24) @dsize as w24from (select w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, p0 * x0 as d00, p0 * x1 as d01, p0 * x2 as d02, p0 * x3 as d03, p0 * x4 as d04, p1 * x0 as d10, p1 * x1 as d11, p1 * x2 as d12, p1 * x3 as d13, p1 * x4 as d14, p2 * x0 as d20, p2 * x1 as d21, p2 * x2 as d22, p2 * x3 as d23, p2 * x4 as d24 from (select w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, x0, x1, x2, x3, x4, y0 - e0/(e0+e1+e2) as p0, y1 - e1/(e0+e1+e2) as p1, y2 - e2/(e0+e1+e2) as p2 from (select w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, x0, x1, x2, x3, x4, y0, y1, y2, exp( w00 * x0 + w01 * x1 + w02 * x2 + w03 * x3 + w04 * x4 ) as e0, exp( w10 * x0 + w11 * x1 + w12 * x2 + w13 * x3 + w14 * x4 ) as e1, exp( w20 * x0 + w21 * x1 + w22 * x2 + w23 * x3 + w24 * x4 ) as e2 from data, weight) t1 )t2 )t3;
下面就是核心部分,我们使用 Recursive CTE 来进行迭代训练:+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+| w00 | w01 | w02 | w03 | w04 | w10 | w11 | w12 | w13 | w14 | w20 | w21 | w22 | w23 | w24 |+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+| 0.242000022455130986666666666667 | 0.199736070114635900000000000000 | 0.135689102774125773333333333333 | 0.104372938417325687333333333333 | 0.128775320011717430666666666667 | 0.296128284590438133333333333333 | 0.237124925707748246666666666667 | 0.281477497498236260000000000000 | 0.225631554555397960000000000000 | 0.215390025342499213333333333333 | 0.061871692954430866666666666667 | 0.163139004177615846666666666667 | 0.182833399727637980000000000000 | 0.269995507027276353333333333333 | 0.255834654645783353333333333333 |+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+----------------------------------+1 row in set (0.03 sec)
核心的思路是,每次迭代的输入都是上一次迭代的结果,然后我们再加一个递增的迭代变量来控制迭代次数,大体的架构:mysql> set @num_iterations = 1000;Query OK, 0 rows affected (0.00 sec)
接着,我们把一次迭代的 SQL 和这个迭代的框架结合起来(为了提高计算精度,在中间结果里加入了一些类型转换):with recursive cte(iter, weight) as(select 1, init_weightunion allselect iter+1, new_weightfrom cte where ites < @num_iterations)
这个版本和上面迭代一次的版本的区别在于两点:with recursive weight( iter, w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24) as(select 1, cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast (0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30)), cast(0.1 as DECIMAL(35, 30))union allselect iter + 1, w00 + @lr * cast(sum(d00) as DECIMAL(35, 30)) @dsize as w00, w01 + @lr * cast(sum(d01) as DECIMAL(35, 30)) @dsize as w01, w02 + @lr * cast(sum(d02) as DECIMAL(35, 30)) @dsize as w02, w03 + @lr * cast(sum(d03) as DECIMAL(35, 30)) @dsize as w03, w04 + @lr * cast(sum(d04) as DECIMAL(35, 30)) @dsize as w04 , w10 + @lr * cast(sum(d10) as DECIMAL(35, 30)) @dsize as w10, w11 + @lr * cast(sum(d11) as DECIMAL(35, 30)) @dsize as w11, w12 + @lr * cast(sum(d12) as DECIMAL(35, 30)) @dsize as w12, w13 + @lr * cast(sum(d13) as DECIMAL(35, 30)) @dsize as w13, w14 + @lr * cast(sum(d14) as DECIMAL(35, 30)) @dsize as w14, w20 + @lr * cast(sum(d20) as DECIMAL(35, 30)) @dsize as w20, w21 + @lr * cast(sum(d21) as DECIMAL(35, 30)) @dsize as w21, w22 + @lr * cast(sum(d22) as DECIMAL(35, 30)) @dsize as w22, w23 + @lr * cast(sum(d23) as DECIMAL(35, 30)) @dsize as w23, w24 + @lr * cast(sum(d24) as DECIMAL(35, 30)) @dsize as w24 from (select iter, w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, p0 * x0 as d00, p0 * x1 as d01, p0 * x2 as d02, p0 * x3 as d03, p0 * x4 as d04, p1 * x0 as d10, p1 * x1 as d11, p1 * x2 as d12, p1 * x3 as d13, p1 * x4 as d14, p2 * x0 as d20, p2 * x1 as d21, p2 * x2 as d22, p2 * x3 as d23, p2 * x4 as d24 from (select iter, w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, x0, x1, x2, x3, x4, y0 - e0/(e0+e1+e2) as p0, y1 - e1/(e0+e1+e2) as p1, y2 - e2/(e0+e1+e2) as p2 from (select iter, w00, w01, w02, w03, w04, w10, w11, w12, w13, w14, w20, w21, w22, w23, w24, x0, x1, x2, x3, x4, y0, y1, y2, exp( w00 * x0 + w01 * x1 + w02 * x2 + w03 * x3 + w04 * x4
) as e0,
exp(
w10 * x0 + w11 * x1 + w12 * x2 + w13 * x3 + w14 * x4
) as e1,
exp(
w20 * x0 + w21 * x1 + w22 * x2 + w23 * x3 + w24 * x4
) as e2
from data, weight where iter < @num_iterations) t1
)t2
)t3
having count(*) > 0
)
select * from weight where iter = @num_iterations;
- 在 data join weight 后,我们增加一个 where iter < @num_iterations 用于控制迭代次数,并且在最后的输出中增加了一列 iter + 1 as ite;
- 最后我们还增加了 having count(*) > 0 ,避免当最后没有输入数据时,aggregation 还是会输出数据,导致迭代不能结束。
然后我们得到结果:
啊这……recursive cte 竟然不允许在 recursive part 里有子查询!不过把上面的子查询全部都合并到一起也不是不可以,那我手动合并一下,然后再试一下:ERROR 3577 (HY000): In recursive query block of Recursive Common Table Expression 'weight', the recursive table must be referenced only once, and not in any subquery
ERROR 3575 (HY000): Recursive Common Table Expression 'cte' can contain neither aggregation nor window functions in recursive query block
不允许子查询我可以手动改 SQL,但是不允许用 aggregate function 我是真的没办法了!
在这里我们只能宣布挑战失败…诶,为啥我不能去改一下 TiDB 的实现呢?
根据 proposal 中的介绍,recursive CTE 的实现并没有脱离 TiDB 基本的执行框架,咨询了 @wjhuang2016 之后,得知之所以不允许使用子查询和 aggregate function 的原因应该有两点:
MySQL 也不允许
如果允许的话,有很多的 corner case 需要处理,非常的复杂
下面我们再次执行一遍:
+------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+
| iter | w00 | w01 | w02 | w03 | w04 | w10 | w11 | w12 | w13 | w14 | w20 | w21 | w22 | w23 | w24 |
+------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+
| 1000 | 0.988746701341992382020000000002 | 2.154387045383744124308666666676 | -2.717791657467537500866666666671 | -1.219905459264249309799999999999 | 0.523764101056271250025665250523 | 0.822804724410132626693333333336 | -0.100577045244777709968533333327 | -0.033359805866941626546666666669 | -1.046591158370568595420000000005 | 0.757865074561280001352887284083 | -1.511551425752124944953333333333 | -1.753810000138966371560000000008 | 3.051151463334479351666666666650 | 2.566496617634817948266666666655 | -0.981629175617551201349829226980 |
+------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+-----------------------------------+-----------------------------------+----------------------------------+----------------------------------+-----------------------------------+
成功了!我们得到了迭代 1000 次后的参数!
下面我们用新的参数来重新计算正确率:
这次正确率到达了 98%。+-------------------------------------------------+
| sum(y0 = r0 and y1 = r1 and y2 = r2) / count(*) |
+-------------------------------------------------+
| 0.9867 |
+-------------------------------------------------+
1 row in set (0.02 sec)
Conclusion
我们这次成功使用纯 SQL 在 TiDB 中训练了一个 Softmax logistic regression model,主要利用了 TiDB v5.1 版本的 Recursive CTE 功能。在测试的过程中,我们发现了目前 TiDB 的 Recursive CTE 不允许存在 subquery 和 aggregate function,我们简单修改了 TiDB 的代码,绕过了这个限制,最终成功训练出了一个模型,并在 iris dataset 上得到了 98% 的准确率。Discussion
- 经过一些测试后,发现 PostgreSQL 和 MySQL 均不支持在 Recursive CTE 使用聚合函数,可能实现起来确实存在一些难以处理的 corner case,具体大家可以讨论一下。
- 本次的尝试,是手动把所有的维度全部展开,实际上我还写了一个不需要展开所有维度的实现(例如 data 表的 schema 是 (idx, dim, value)),但是这种实现方式需要 join 两次 weight 表,也就是在 CTE 里需要递归访问两次,这还需要修改 TiDB Executor 的实现,所以就没有写在这里。但实际上,这种实现方式更加的通用,一个 SQL 可以处理所有维度数量的模型(我最初想尝试用 TiDB 训练 MINIST)。

 随时随地看视频
随时随地看视频




