之前因为工作原因接触了很多有意思的算法知识,为了巩固大家的算法基础和编程能力,笔者总结了8道算法题, 供大家学习参考. 接下来我们来看看题目.
1. 有一个数组arr = [a1, a2, a3, b1, b2, b3, c1, c2, c3…], 通过算法将数组进行拆分, 转化为如下格式的数组a1, b1, c1], [a2, b2, c2], [a3, b3, c3]并实现通用公式.
参考答案:
/**
* arr 待排序数组
* result 计算的结果数组
*/
function rangeArr(arr = [], result = []) {
arr.forEach(item => {
let i = /\d*$/.exec(item)[0]
result[i] ? result[i].push(item) : (result[i] = [item])
})
return result.filter(Boolean)
}
2. 假设集合A={a, b},集合B={0, 1, 2},则两个集合的笛卡尔积为{(a, 0), (a, 1), (a, 2), (b, 0), (b, 1), (b, 2)}。求当A={a, b, …, n}, B={0, 1, 2, …, n}时的笛卡尔积.
笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尓积,又称直积,表示为X × Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员 。
参考答案:
/*
* @Author: Mr Jiang.Xu
* @Date: 2019-08-31 00:05:33
* @Last Modified by: Mr Jiang.Xu
* @Last Modified time: 2019-08-31 00:05:33
*/
function cartesian(arr) {
if (arr.length < 2) return arr[0] || [];
return [].reduce.call(arr, function (col, set) {
let res = [];
col.forEach(c => {
set.forEach(s => {
let t = [].concat(Array.isArray(c) ? c : [c]);
t.push(s);
res.push(t);
})
});
return res;
});
}
3. 原生js实现一个Set数据类型, 并实现集合的差集, 并集, 补集, 交集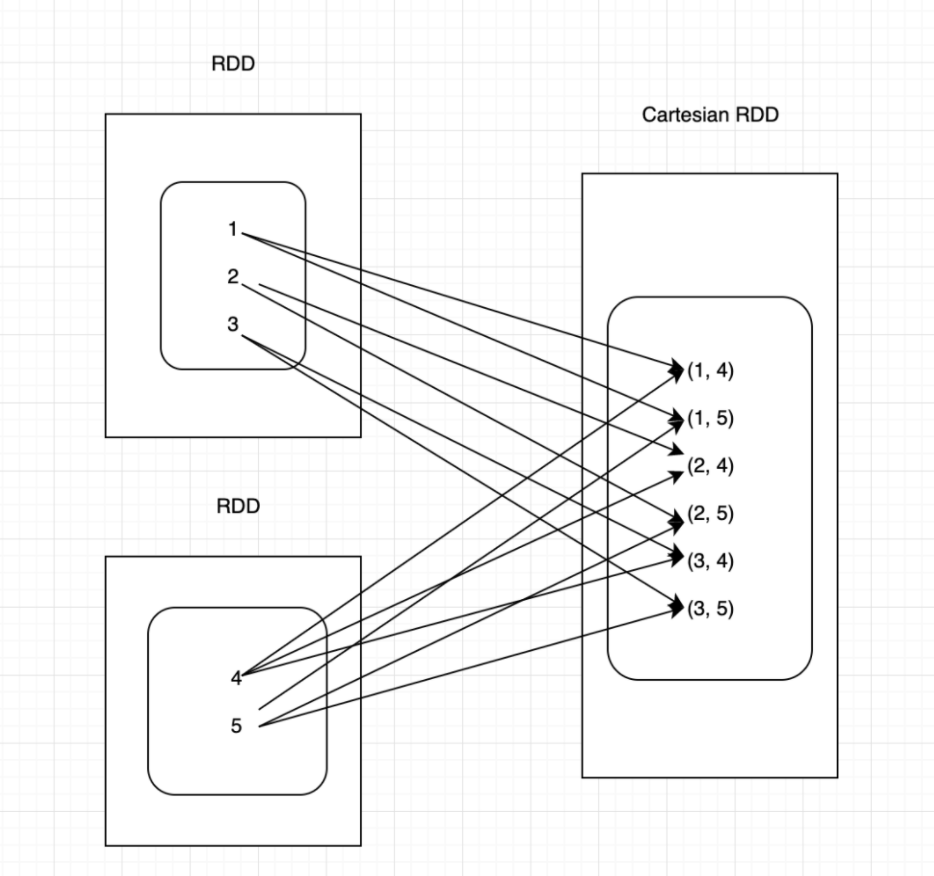
// 创建集合,并实现交集,差集,补集,并集
function MySet() {
let items = {}
// 判断值是否存在
this.has = function(val) {
return val in items
}
// 添加
this.add = function(val) {
if(!this.has(val)) {
items[val] = val
return true
}
return false
}
// 移除
this.remove = function(val) {
if(this.has(val)) {
delete items[val]
return true
}
return false
}
// 清空
this.clear = function() {
items = {}
}
// 大小
this.size = function() {
return Object.keys(items).length
}
// 取值
this.values = function() {
return Object.keys(items)
}
// 并集
this.union = function(otherSet) {
let unionSet = new Set()
let values = this.values()
for(let i=0; i < values.length; i++) {
unionSet.add(values[i])
}
values = otherSet.values()
for(let i=0; i < values.length; i++) {
unionSet.add(values[i])
}
return unionSet
}
// 交集
this.intersection = function(otherSet) {
let intersectionSet = new Set()
let values = this.values()
for(let i=0; i<values.length; i++) {
if(otherSet.has(values[i])) {
intersectionSet.add(values[i])
}
}
return intersectionSet
}
// 差集
this.difference = function(otherSet) {
let differenceSet = new Set()
let values = this.values()
for(let i = 0; i < values.length; i++) {
if(!otherSet.has(values[i])) {
differenceSet.add(values[i])
}
}
return differenceSet
}
// 子集
this.subset = function(otherSet) {
if(this.size() > otherSet.size()) {
return false
}else {
let values = this.values()
for(let i=0; i<values.length; i++) {
if(!otherSet.has(values[i])) {
return false
}
}
return true
}
}
}
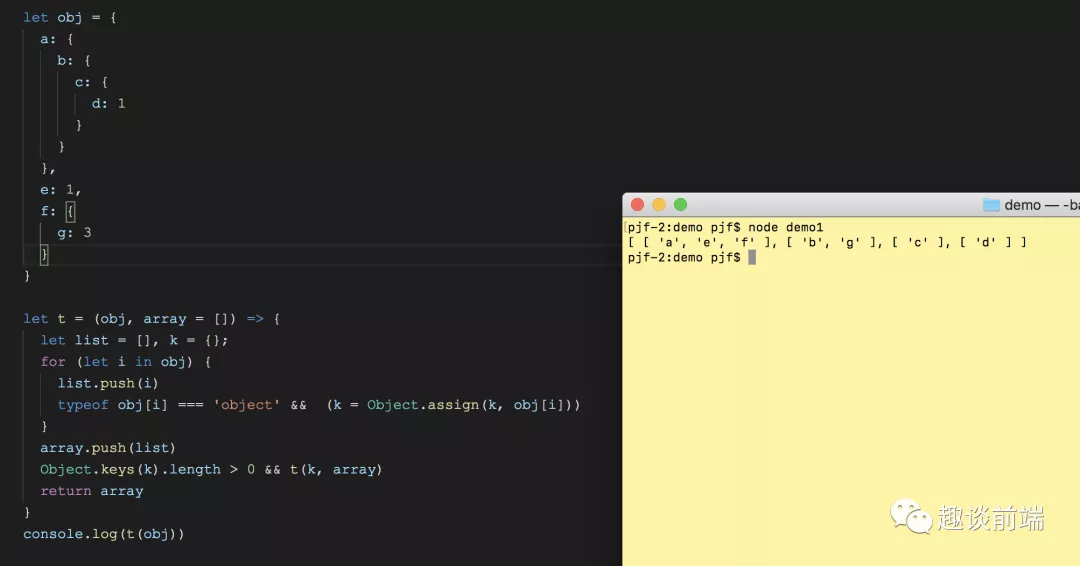
4. 给定一个任意嵌套结构的对象如下,使用你熟悉的算法,将对象的属性按照层级输出到一个数组中.如下:

参考答案: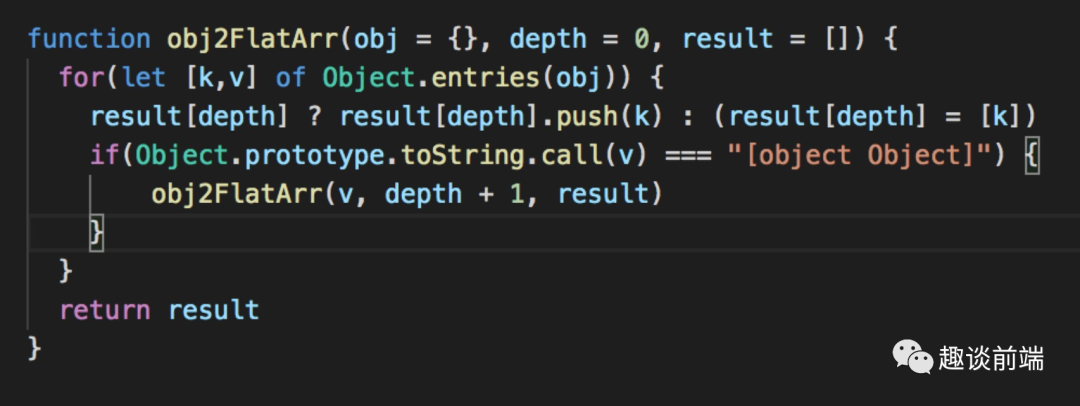
更多优质答案:
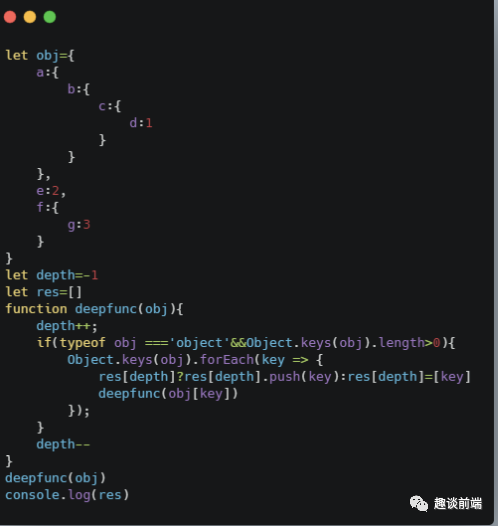
5.找出数字数组中出现多次的数字,比如[1,2,2,3,4,5,4] => [2,4]

其他优质答案:
对这个问题的进一步扩展,比如说我不仅要求重复的数字,我还要计算出出现次数最多的数字呢?笔者写了一个方法,供大家参考: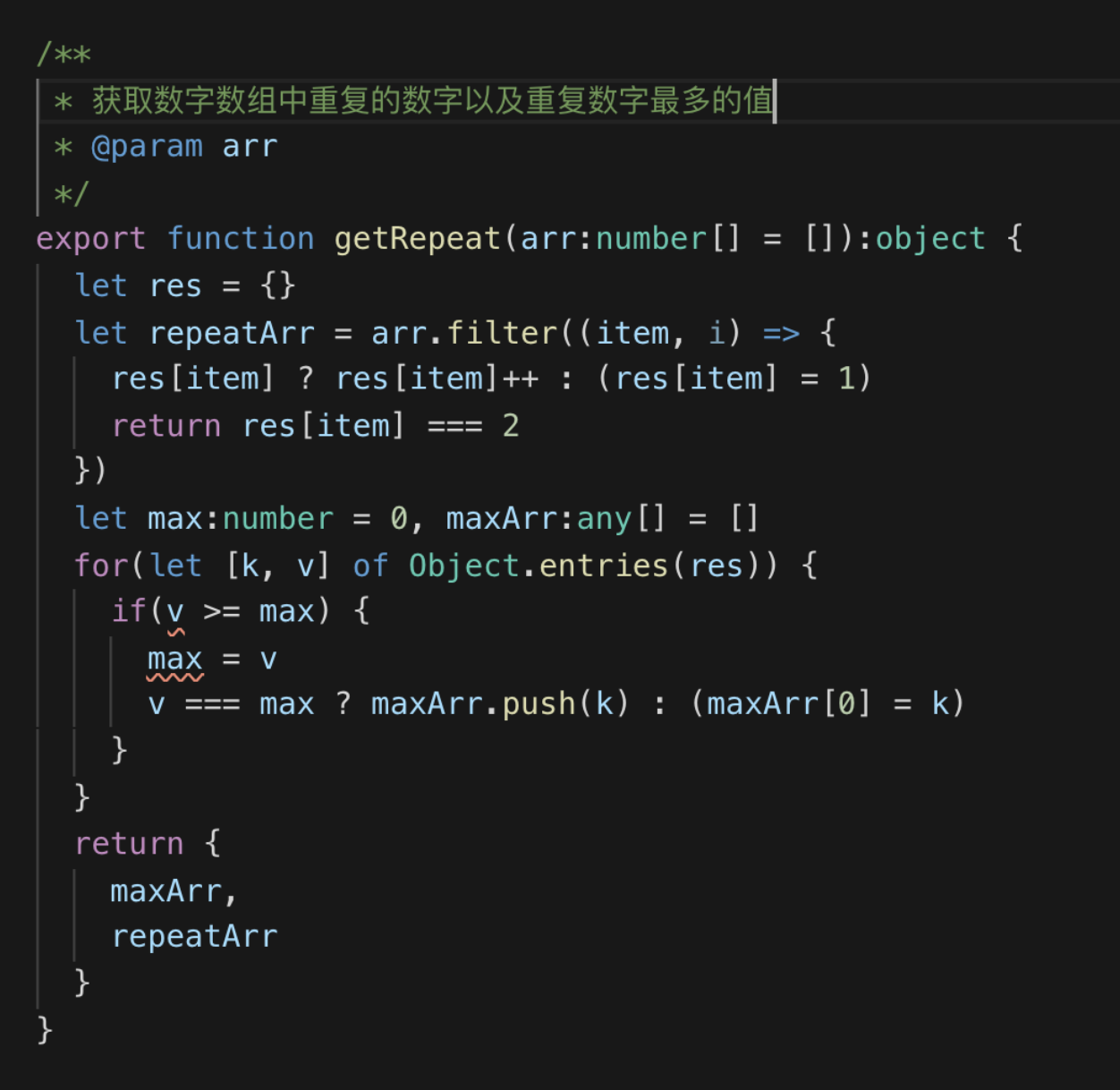
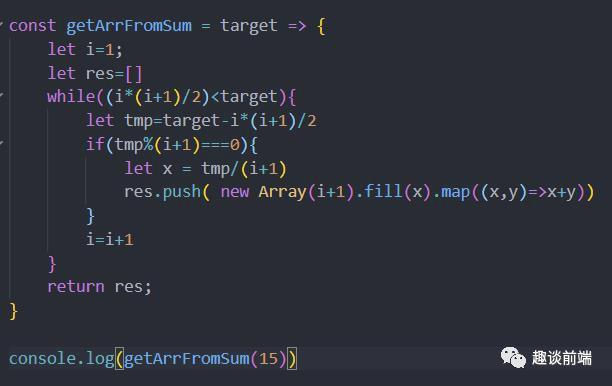
6. 输入一个正数N, 输出所有和为N的连续正数序列. 例如输入15, 结果: [[1, 2, 3, 4, 5], [4, 5, 6], [7, 8]].
[优质解法]
7. 已知圆的半径为1, 用javascript算法, 实现每次都返回不同的坐标值, 且坐标值都在圆内.
[参考解法]
function generateRandomPos() {
// 缓存已存在坐标
const cache = {}
// 圆形边界
const boundRect = [-1, 1]
// 生成在-1到1的随机值
const random = () => boundRect[+(Math.random() > 0.5)] * Math.random()
return generate()
function generate() {
// 生成x,y坐标
let x = random(),
y = random()
// 根据勾股定理,xy的平方和应小于等于1(圆形坐标关系),并且之前没有生成同样的坐标
if(Math.pow(x, 2) + Math.pow(y, 2) <= 1 && !cache[`${x}${y}`]) {
return cache[`${x}${y}`] = [x, y]
}else {
return generate()
}
}
}
8. 用原生javasctript实现一个虚拟dom及其基本渲染api.
[参考解法]
实现步骤:
- 用 JavaScript 对象结构表示 DOM 树的结构;然后用该对象构建一个真正的 DOM 树,插到文档中
- 当状态变更的时候,重新构造一棵新的对象树。然后用新的树和旧的树进行比较,记录两棵树的差异
- 把第二步所记录的差异应用到步骤1所构建的真正的DOM树上,视图更新
Virtual DOM 本质就是在 JS 和 DOM 之间做了一个缓存, 实现代码如下:
// 定义虚拟元素
function Element (tagName, props, children) {
this.tagName = tagName
this.props = props
this.children = children
}
// 渲染方法
Element.prototype.render = function () {
let el = document.createElement(this.tagName) // 根据tagName构建
let props = this.props
for (let propName in props) { // 设置节点的DOM属性
let propValue = props[propName]
el.setAttribute(propName, propValue)
}
let children = this.children || []
children.forEach(function (child) {
let childEl = (child instanceof Element)
? child.render() // 如果子节点也是虚拟DOM,递归构建DOM节点
: document.createTextNode(child) // 如果字符串,只构建文本节点
el.appendChild(childEl)
})
return el
}
// 更新逻辑
Element.prototype.updateElement = function (root, newEl, oldEl, index = 0) {
if (!oldEl){
root.appendChild(newEl.render());
} else if (!newEl) {
root.removeChild(root.childNodes[index]);
} else if ((typeof newEl !== typeof oldEl) ||
(typeof newEl === 'string' && newEl !== oldEl) ||
(newEl.type !== oldEl.type)) {
if (typeof newEl === 'string') {
root.childNodes[index].textContent = newEl;
} else {
root.replaceChild(newEl.render(), root.childNodes[index]);
}
} else if (newEl.tagName) {
let newLen = newEl.children.length;
let oldLen = oldEl.children.length;
for (let i = 0; i < newLen || i < oldLen; i++) {
this.updateElement(root.childNodes[index], newEl.children[i], oldEl.children[i], i)
}
}
}






 随时随地看视频
随时随地看视频