演示地址:点击查看演示
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。因此各个阶段决策的选取不能任意确定,它依赖于当前面临的状态,又影响以后的发展。当各个阶段决策确定后,就组成一个决策序列,因而也就确定了整个过程的一条活动路线.这种把一个问题看作是一个前后关联具有链状结构的多阶段过程就称为多阶段决策过程,这种问题称为多阶段决策问题。在多阶段决策问题中,各个阶段采取的决策,一般来说是与时间有关的,决策依赖于当前状态,又随即引起状态的转移,一个决策序列就是在变化的状态中产生出来的,故有“动态”的含义,称这种解决多阶段决策最优化的过程为动态规划方法。
本期内容:动态规划
动态规划是一种将复杂问题分解成很多子问题并将子问题的求解结果存储起来避免重复求解的一种算法。
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决。动态规划算法的基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
动态规划(dynamic programming)是一种算法设计技术,在20世纪50年代由一位卓越的美国数学家 Richard Bellman所发明的。
一个问题能够使用动态规划算法求解时具有的两个主要性质:
- 第一,交叠子问题
动态规划算法的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受,而搜索算法在时间上却无法承受,所以我们舍空间而取时间
- 第二,最优子结构(最优化原理)
最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
本期通过比较递归法、记忆化搜索算法和打表算法的时间复杂度,讨论动态规划的主要性质–交叠的子问题。
1、动态规划问题中的术语
阶段: 把所给求解问题的过程恰当地分成若干个相互联系的阶段,以便于求解,过程不同,阶段数就可能不同.描述阶段的变量称为阶段变量。在多数情况下,阶段变量是离散的,用k表示。此外,也有阶段变量是连续的情形。如果过程可以在任何时刻作出决策,且在任意两个不同的时刻之间允许有无穷多个决策时,阶段变量就是连续的。
状态: 状态表示每个阶段开始面临的自然状况或客观条件,它不以人们的主观意志为转移,也称为不可控因素。在上面的例子中状态就是某阶段的出发位置,它既是该阶段某路的起点,同时又是前一阶段某支路的终点。
无后效性: 我们要求状态具有下面的性质:如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响,所有各阶段都确定时,整个过程也就确定了。换句话说,过程的每一次实现可以用一个状态序列表示,在前面的例子中每阶段的状态是该线路的始点,确定了这些点的序列,整个线路也就完全确定。从某一阶段以后的线路开始,当这段的始点给定时,不受以前线路(所通过的点)的影响。状态的这个性质意味着过程的历史只能通过当前的状态去影响它的未来的发展,这个性质称为无后效性 。
决策: 一个阶段的状态给定以后,从该状态演变到下一阶段某个状态的一种选择(行动)称为决策。在最优控制中,也称为控制。在许多问题中,决策可以自然而然地表示为一个数或一组数。不同的决策对应着不同的数值。描述决策的变量称决策变量,因状态满足无后效性,故在每个阶段选择决策时只需考虑当前的状态而无须考虑过程的历史。
决策变量的范围称为允许决策集合 。
策略: 由每个阶段的决策组成的序列称为策略。对于每一个实际的多阶段决策过程,可供选取的策略有一定的范围限制,这个范围称为允许策略集合
2、交叠子问题(或重叠子问题)
同分治法(Divide and Conquer)一样,动态规划也是将子问题的求解结果进行合并,其主要用在当子问题需要一次又一次地重复求解时,将子问题的求解结果存储到一张表中(称为动态规划表)以免重复计算。因此当没有公共的(交叠的、重叠的)子问题时动态规划算法并不适用,因为没有必要将一个不再需要的结果存储起来。例如,二分搜索(折半查找)就不具有重叠的子问题性质。
我们以下面的递归求解斐波那契数列的问题为例子,就会发现有很多子问题一次又一次地被重复求解。
/*求解斐波那契数列的递归算法 */
int fib(int n) {
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
下图是求解fib(5)的递归树:
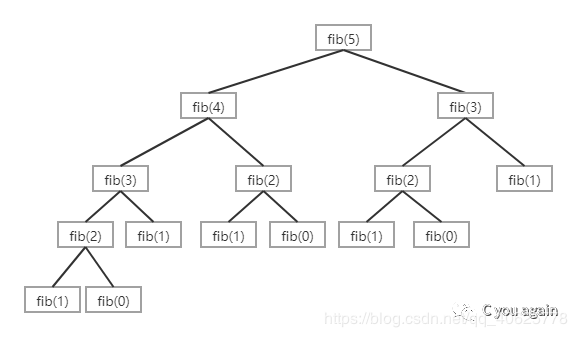
从上面的递归树我们可以发现fib(3)被调用了2次。如果我们在第1次计算fib(3)时将fib(3)的结果存储起来,这样我们在第2次调用fib(3)时就可以使用先前存储的值,而不需要再次计算fib(3)了。下面是两种存储fib(3)值的方法,这两种方法都可以重复使用存储的值:
1、记忆化搜索方法(自顶向下)
说明:所谓顶就是我们要求解的问题,这里就是fib(n)。
采用这种方法,只需对递归程序进行一点小小的修改,即在计算某个值时,先查询一个表。这个表可以使用数组来实现,初始时把数组的值全部初始为NIL(比如-1或0等值,这个值是计算过程中不会出现的那些值)。任何时候当我们需要求解一个子问题时,我们首先查询这个表,如果这个表中有我们预先对该子问题求解的结果,则我们直接返回表中的这个值,否则我们就对子问题进行计算,并把计算结果存入这个表中,以便在后续计算中可以重复使用。
下面的程序是求解第n个斐波那契数的记忆化搜索版本:
/* 求解第n个斐波那契数的记忆化搜索程序 */
#include<stdio.h>
#define NIL -1
#define MAX 100
int lookup[MAX]; /* 用数组实现的查找表 */
/* 将查找表初始化为NIL */
void _initialize() {
int i;
for (i = 0; i < MAX; i++)
lookup[i] = NIL;
}
/* 求解第n个斐波那契数 */
int fib(int n) {
if (lookup[n] == NIL) {/* 如果为NIL,表明第n项没有求解过 */
if (n <= 1)
lookup[n] = n; /* 求解第n项,并把求解结果存入查找表 */
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n]; /* 如果不为NIL,表明第n项求解过,直接返回 */
}
int main() {
int n = 40;
_initialize();
printf("Fibonacci number is %d ", fib(n));
return 0;
}
2、打表法(自底向上)
用打表法求解一个问题时,使用自底向上的方式进行计算并返回表格中的最后一项。例如,同样是计算第n个斐波那契数,首先计算fib(0),然后计算fib(1),再计算fib(2),计算fib(3),直到fib(n)。因此,我们采用的是自底向上的方式逐一建立子问题的求解结果表的。
下面是打表法求解第n个斐波那契数的程序。(所谓打表法,就是把计算结果制成表格,然后打印结果,简称打表法,也称制表法。)
/* 打表法 */
#include<stdio.h>
int fib(int n) {
int f[n + 1];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
int main() {
int n = 9;
printf("Fibonacci number is %d ", fib(n));
return 0;
}
打表法和记忆化搜索法都是把子问题的求解结果存入表格。在记忆化搜索方法中,我们只是在需要时往查询表中添加记录,而在打表法中,从第1项记录开始,所有计算结果一项一项地添加到表中。与打表法不同,记忆化搜索方法无需将所有计算结果添加到查询表中。
人们往往从时间复杂度和空间复杂度两个方面来衡量某个算法的优劣性,但在实际生活中,如果对某个算法的要求不是特别高,我们一般只考虑算法的时间复杂度。下面通过比较递归法、记忆化搜索方法、打表法在求解第n项斐波那契数时的时间开销来分析算法的优劣性。
递归方法:
#include<stdio.h>
#include<time.h>
/* 求解斐波那契数列的递归算法 */
int fib(int n) {
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main() {
int n = 40;
clock_t begin, end;
double time_spent;
begin = clock(); /* 开始时间 */
printf("Fibonacci number is %d\n", fib(n));
end = clock(); /* 结束时间 */
time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
printf("Time Taken %lf\n", time_spent);
return 0;
}
运行结果: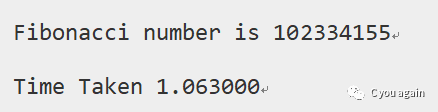
注意:上面的时间在不同的机器上是不同的
记忆化搜索方法:
/* 求解第n个斐波那契数的记忆化搜索程序 */
#include<stdio.h>
#include<time.h>
#define NIL -1
#define MAX 100
int lookup[MAX]; /* 用数组实现的查找表 */
/* 将查找表初始化为NIL */
void _initialize() {
int i;
for (i = 0; i < MAX; i++)
lookup[i] = NIL;
}
/* 求解第n个斐波那契数 */
int fib(int n) {
if (lookup[n] == NIL) {/* 如果为NIL,表明第n项没有求解过 */
if (n <= 1)
lookup[n] = n; /* 求解第n项,并把求解结果存入查找表 */
else
lookup[n] = fib(n - 1) + fib(n - 2);
}
return lookup[n]; /* 如果不为NIL,表明第n项求解过,直接返回 */
}
int main() {
int n = 40;
clock_t begin, end;
double time_spent;
_initialize();
begin = clock(); /* 开始时间 */
printf("Fibonacci number is %d\n", fib(n));
end = clock(); /* 结束时间 */
time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
printf("Time Taken %lf\n", time_spent);
return 0;
}
运行结果: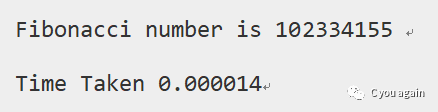
注意:上面的时间在不同的机器上是不同的
打表法:
#include<stdio.h>
#include<time.h>
/* 打表法 */
#include<stdio.h>
int fib(int n) {
int f[n + 1];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
f[i] = f[i - 1] + f[i - 2];
return f[n];
}
int main() {
int n = 40;
clock_t begin, end;
double time_spent;
begin = clock(); /* 开始时间 */
printf("Fibonacci number is %d\n", fib(n));
end = clock(); /* 结束时间 */
time_spent = (double)(end - begin) / CLOCKS_PER_SEC;
printf("Time Taken %lf\n", time_spent);
return 0;
}
运行结果: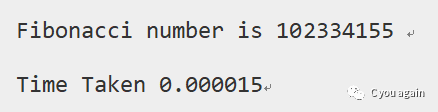
注意:上面的时间在不同的机器上是不同的
通过比较三种方法所花费的时间,很明显递归方法比记忆化搜索方法和打表法这两种采用动态规划方法所花费的时间都大很多。
3、最优子结构
对于一个给定的问题,当该问题可以由其子问题的最优解获得时,则该问题具有“最优子结构”性质。
例如,“最短路径”问题具有如下的“最优子结构”性质:
如果一个结点x在从起点u到终点v的最短路径上,则从u到v的最短路径由从u到x的最短路径和从x到v的最短路径构成。像Floyd-Warshall(弗洛伊德—沃舍尔)和Bellman-Ford(贝尔曼—福特)算法就是典型的动态规划的例子。
另外,“最长路径”问题不具有“最优子结构”性质。我们这里所说的最长路径是两个节点之间的最长简单路径(路径没有环),由CLRS(Thomas H. Cormen,Charles E. Leiserson,Ronald L. Rivest,Clifford Stein)编写的《算法导论》(Introduction to Algorithms)这本书中给出了下面的无权图。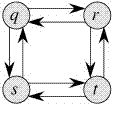
从q到t有两条最长的路径:q→r→t与q→s→t。与最短路径不同,这些最长路径没有“最优子结构”性质。例如,最长路径q→r→t不是由q 到r的最长路径和r到t的最长路径构成的,因为从q到r的最长路径是 q→s→t→r,从r到t的最长路径是r→q→s→t。
经典例题:数字三角形
题目描述:
下图给出了一个数字三角形,从三角形的顶部到底部有很多条不同的路径,对于每条路径,把路径上面的数加起来可以得到一个和,你的任务就是找到最大的和。
注意:路径上的每一步只能从一个数走到下一层上和它最近的左边的那个数或者右边的那个数。
输入:
输入一个正整数N (1 < N <= 100),给出三角形的行数,下面的N行给出数字三角形,数字三角形上的数的范围都在0和100之间。
输出:
输出最大的和。
样例输入:
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
样例输出:
30
解题思路:
动态规划通常用来求最优解。能用动态规划解决的求最优解问题,必须满足最优解的每个局部解也都是最优的。以上题为例,最佳路径中的每个数字到底部的那一段路径,都是从该数字出发到底部的最佳路径。
实际上,递归的思想在编程时未必要实现为递归函数。在上面的例子中,有递推公式: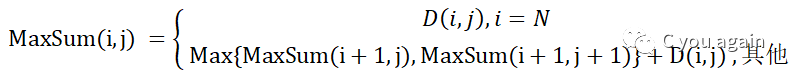
不需要写递归函数,从最后一行的元素开始向上逐行递推,就能求得最终 dp[1][1]的值。程序如下:
#include<stdio.h>
#include<string.h>
#define MAX_NUM 1000
int D[MAX_NUM + 10][MAX_NUM + 10]; /* 存储数字三角形 */
int N; /* 数字三角形的行数 */
int dp[MAX_NUM + 10][MAX_NUM + 10]; /* 状态数组 */
int max(int x, int y) {
return x > y ? x : y;
}
int main() {
int i, j;
scanf("%d", &N);
memset(dp, 0, sizeof(dp));/* 状态数组全部初始化为0 */
for (i = 1; i <= N; ++i)
for (j = 1; j <= i; ++j)
scanf("%d", &D[i][j]); /* 输入数字三角形 */
for (j = 1; j <= N; j++) { /* 处理最底层一行 */
dp[N][j] = D[N][j]; /* 最底层一行状态数组的值即为该数字本身 */
}
for (i = N - 1; i >= 1; i--) { /* 从倒数第二层开始直至最顶层 */
for (j = 1; j <= i; j++) {
dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + D[i][j];
}
}
printf("%d\n", dp[1][1]); /* 顶点(1,1)即为最大值 */s
return 0;
}
如下图所示,方框里的数字是能取得的最大值。相信大家看完这个图,对动态规划的理解不那么困难了。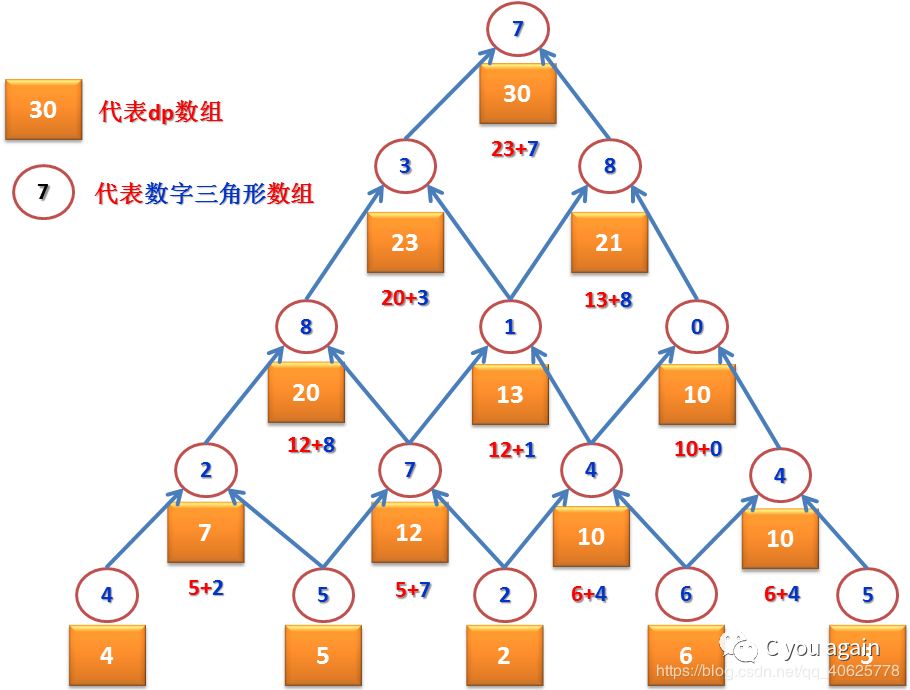
实际上,因为dp[i][j]的值在用来计算出dp[i-1][j]后已经无用,所以可以将计算出的dp[i-1][j]的值直接存放在dp[i][j]的位置。这样,计算出 dp[N-1][1]替换原来的 dp[N][1],计算出 dp[N-1][2]替换原来的dp[N][2]…计算出 dp[N-1][N-1]替换原来的 dp[N][N-1],dp数组实际上只用最后一行,就能够存放上面程序中本该存放在dp[N-1]那一行的全部结果。同理,再一行行向上递推,dp数组只需要最后一行就可以存放全部中间计算结果,最终的结果(本该是dp[1][1])也可以存放在dp[N][1])。因此,实际上dp不需要是二维数组,一维数组就足够了。
改写后的程序如下:
#include<stdio.h>
#include<string.h>
#define MAX_NUM 1000
int D[MAX_NUM + 10][MAX_NUM + 10]; /* 存储数字三角形 */
int N; /* 数字三角形的行数 */
int *dp; /* 状态数组 */
int max(int x, int y) {
return x > y ? x : y;
}
int main() {
int i, j;
scanf("%d", &N);
for (i = 1; i <= N; ++i)
for (j = 1; j <= i; ++j)
scanf("%d", &D[i][j]); /* 输入数字三角形 */
dp = D[N]; /* dp指向第N行 */
for (i = N - 1; i >= 1; i--) { /* 从倒数第二层开始直至最顶层 */
for (j = 1; j <= i; j++) {
dp[j] = max(dp[j], dp[j + 1]) + D[i][j];
}
}
printf("%d\n", dp[1]); /* (1,1)即为最大值 */
return 0;
}
这种用一维数组取代二维数组进行递推、节省空间的技巧叫“滚动数组”。上面的程序虽然节省了空间,但是没有降低时间复杂度,时间复杂度依然是O(N^2)的,从程序使用了两重循环就可以看出。
4、总结
许多求最优解的问题可以用动态规划来解决。用动态规划解题,首先要把原问题分解为若干个子问题,这一点和前面的递归方法类似。区别在于,单纯的递归往往会导致子问题被重复计算,而用动态规划的方法,子问题的解一旦求出就会被保存,所以每个子问题只需求解一次。
子问题经常和原问题形式相似,有时甚至完全一样,只不过规模从原来的n变成n-1, 或从原来的n×m变成n×(m-1)。找到子问题,就意味着找到了将整个问题逐渐分解的办法,因为子问题可以用相同的思路一直分解下去,直到最底层规模最小的子问题可以一目了然地看出解(像上面数字三角形的递推公式中,当i=N时,解就可以直接得到)。每一层子问题的解决会导致上一层子问题的解决,逐层向上,就会导致最终整个问题的解决。如果从最底层的子问题开始,自底向上地推导出一个个子问题的解,那么编程时就不需要写递归函数了。

 随时随地看视频
随时随地看视频




