翻译《计算机科学与数学》第一章第六节：证明“当且仅当”

许多数学定理这样断言两个陈述在逻辑上相等，即一个陈述成立当且仅当另一个陈述成立。有一个几千年来被熟知的例子：当且仅当两个三角形的两边及两边的夹角相等，这两个三角形的边长相等。

‌

短语”当且仅当“经常出现，通常被简写为”iff“。

1.6.1 方法一：证明每个陈述蕴含另一个

陈述”P当且仅当Q“等同于两个表述”P蕴含Q“和”Q当且仅当P“。

所以通过证明两个蕴含式来证明”当且仅当“：

‌

1. 写下，”我们证明P蕴含Q，反之亦然“。

2. 写下，”首先，我们证明P蕴含Q“。通过章节1.5中的方法证明。

3. 写下，”现在，我们证明Q蕴含P“。再通过章节1.5中的方法证明。

   
   

1.6.2 方法二：构建一系列当且仅当

为了证明当且仅当Q为真，P为真：

‌

1. 写下，”我们构建一系列当且仅当的蕴含式“。

2. 证明 P 等价于第二个陈述，第二个陈述等同于第三个陈述，以此类推直到Q。

‌

这个方法有时候比方法一需要更多聪明才智，但是结果可能得到一个简短优雅的证明。

‌

例子

‌

一系列值x1,x2,...,xnx_1,x_2,...,x_nx1,x2,...,xn 的标准差被定义为：

‌

μ 是平均值或者值的平均数：

定理 1.6.1。当且仅当所有的值等于平均值，一系列值 x1,...,xnx_1,...,x_nx1,...,xn 的标准差等于0.

‌

例如，当且仅当每个人的得分确切地等于班级平均值，考试分数的标准差为0。

‌

证明。我们构建一系列“当且仅当”的蕴含式，以标准差（1.3）等于0开始：

现在因为对于平方根为0的某个数而言，0是唯一的数值，所以等式（1.4）成立，当且仅当

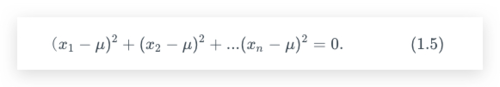
实数的配方总是为非负数，所以等式左边的每一项是非负数。这就意味着（1.5）成立，当且仅当

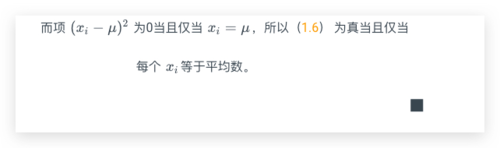
                    （1.5）左手边的每一项是0.                                 （1.6）