纯CSS实现动态图片的九宫格布局

起因

最近碰到这样一个需求，要实现一个“九宫格图片”展示，设计师给过来的稿子是酱的

是的，九宫格对应的是九种样式。

---

天不怕，地不怕，就怕设计有想法。

当一看到这样的需求，很多人的第一反应应该是会JS一把梭，通过一系列的判断条件来修改图片宽高或者更改DOM元素的class。的确，这么复杂的样式难免让人望而却步，这个需求通过JS是可以完成的【PS：废话，JS啥干不了】，但是如果只是分享JS如何实现的话，未免太小儿科了。

---

纯CSS实现

作为一个极客，当然一开始是想用纯CSS实现的，相信很多前端对JS非常熟悉甚至精通，但对CSS敢说精通的肯定是少之又少，其中一个原因在于很多人碰到类似这样的复杂样式设计的时候想的都是通过JS修改，所以很多人对CSS的掌握程度还不够深入。其实CSS是非常强大的，有必要深入掌握和研究，在此笔者强烈安利《CSS揭秘》这本书，也正是因为这本书才让笔者对CSS有了更深的认识。

---

需求分析

写代码之前先来分析下这个需求：

• 宽高：

1. 1张图【宽320，高320】[2倍稿尺寸]
2. 2张图时【宽332，高332】
3. 3张图、4张图、6张图，7张图、9张图时【宽220，高220】
4. 5张图、8张图时【第4、第5张宽高332】，【其余220】

• 间距：

1. 2张时，【最后一张】只有left方向margin
2. 3张时，【第2张】左右margin
3. 4张时，【第2张】和【最后一张】都只有left方向的margin，【3，4】有top方向的margin
4. 5张时，【最后一张】只有left方向margin
5. 6张、7张时，【第2张、第4张】有左右margin，从【第4张起】top有
6. 8张时，【第2张、第4张】时左右margin，从【第4张起】top有，【最后一张】只有left
7. 9张时，【第2张、第4张、第8张】有左右margin

• 圆角10：

1. 1张图时【都有】圆角
2. 2张图时、3张图-【第1张左上、左下】，【最后一张右上，右下】
3. 4张图时【第1张左上】，【第2张右上】，【第3张左下】，【最后一张右下】
4. 5张图时【第1张左上】，【第3张右上】，【第4张左下】，【最后一张右下】
5. 6张图时【第1张左上】，【第3张右上】，【第4张左下】，【最后一张右下】
6. 7张图时【第1张左上】，【第3张右上】，【第7张左下、右下】
7. 8张图时【第1张左上】，【第3张右上】，【第7张左下】，【最后一张右下】
8. 9张图时【第1张左上】，【第3张右上】，【第7张左下】，【最后一张右下】
   上文就是张数对应的样式。是不是很吓人。实际上，仔细看这个需求就会发现——样式是有一定规律的。

---

归纳法

大家在中学的时候都学过数学的归纳法，就是一个命题先求出n=1的时候成立，然后假设n=k成立，证明n=k+1也成立，从而证得命题在n=k 【k=任意实数】的时候都成立。接下来就是要借用下这个归纳法的技巧来寻找需求中隐藏的规律。

---

宽高

仅列出宽高332的情况及对应的图片索引的时候不难看出当图片索引为：

1. 3n+1且是倒数第2张时
2. 3n+1且是最后一张时
   以上两种情况图片的宽高均应为320；
   剩余两种情况是：
3. 只有一张时宽高320；
4. 其余的情况和索引宽高都为220；
   根据这个规律写出相应的CSS代码为：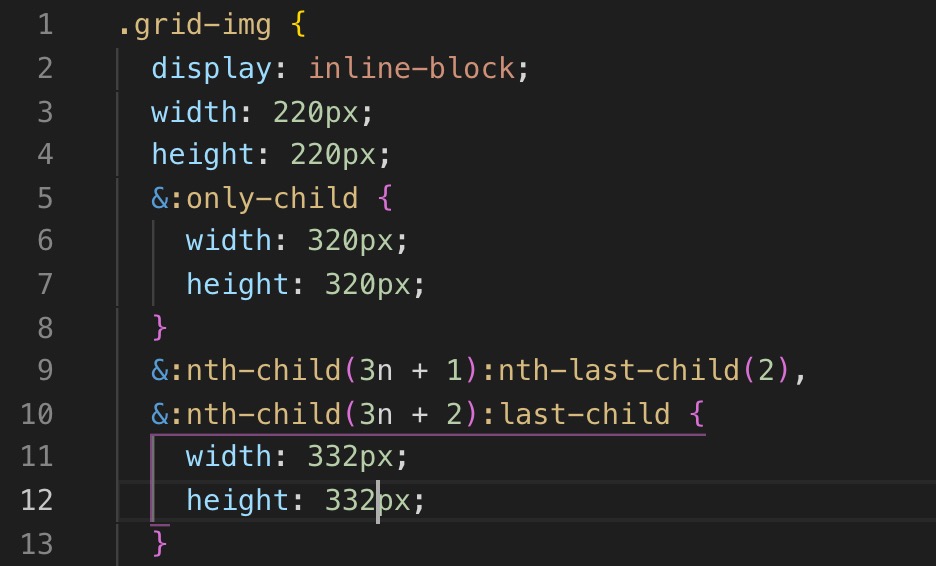
   
   这里主要用到就是CSS的伪类选择器，其实伪类选择器知道人不少，但是很少有人知道伪类选择器是可以联合使用，这里使用的技巧便是《CSS揭秘》中所介绍的伪类选择器联合使用来定位到具体元素，nth-child正向查找，nth-last-child逆向查找，联合意味着取交集，这样便能实现类似【3n+1且是倒数第2张】这样的需求。

---

间距/布局

经过刚刚的分析之后，相信大家已经有了一个基本的认识，这里就不再具体分析，直接上代码




间距规律相对简单，只需处理一些边界情况即可。

---

圆角

圆角算是比较复杂的:

---

最终的代码

至此，我们的九宫格代码就已全部介绍完毕。完整代码如下：

---

DEMO