作者简介
浩彬老撕,R语言中文社区特邀作者。
决策树算法概述
决策树算法,顾名思义,就一颗用于分类的树状决策结构。事实上,决策树算法在业界中的应用是十分的广泛,这不仅仅是因为该算法其具有良好的分类能力更重要的是它具有较强的可解释性,并且直观易懂等特点。实际上,基于决策树的逻辑结构是与人类在现实社会环境中的决策逻辑十分的类似,例如浩彬老撕就在某天在思考一个人生三大问:


该思考过程可以以如下的文字简单表达:
(1) 今天是否周末?如果不是周末则不去,如果是周末则继续思考下一个问题;
(2) 本周的工作是否完成?如果还没有完成则不去,如果已经完成则继续思考下一个问题;
(3) 今天是晴天吗?如果不是晴天则不去,如果是晴天则继续思考下一个问题;
(4) 今天能不能在电影院找到好位置?如果不能找到好位置则不去,如果能找到好位置则决定去电影院看电影;
该思考过程假如以一颗决策树的形式来表达的话就是如下形式:
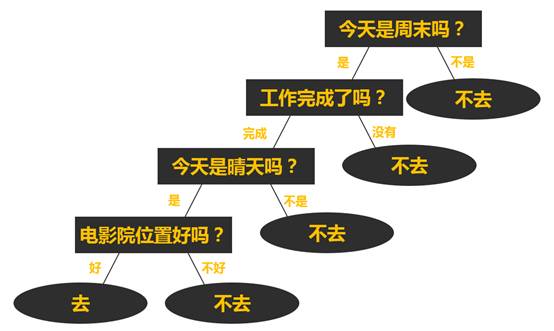
在这个看电影的决策逻辑中,实际上是浩彬老撕通过自己的历史多次看电影的的经历总结而成。决策树算法这种形式实际上是一种根据训练数据集,通过一系列测试问题(形如“今天是周末吗?”)从而输出分类目标进行判断的过程。
决策树这样的表达形式非常的直观且容易理解,一般地,一颗决策树是由一个根节点,若干个内部节点以及若干个叶子节点组成,根节点和内部节点代表相应的测试条件,而叶子节点则代表最终输出结果:
(1) 根节点:根节点位于最上层,代表第一个测试条件,一颗决策树有且只有一个根节点,根节点没有入边,拥有零条或以上的出边;
(2) 内部节点:位于根节点之下,代表一种测试条件。中间节点有一条入边,拥有两条或以上的出边;
(3) 叶子节点:决策树的终端节点,代表决策树的判定结果。叶子节点只有一条入边而没有出边;
可以看到,这种树状的表达形式实际上与前面提到的If-Then规则可以进行相互转换的,其中从根节点出发,到任意一个叶子节点,将形成一条规则:If“今天是周末吗”=“False”,Then“不去”。值得注意的是,通过决策树所形成的规则应当是互斥且完备的,即对于任意一个样本数据,有且只有一条规则与其一一对应输出分类结果。
决策树的生成
在实际应用过程中,我们不仅仅只针对一个样本,我们是希望从大量的数据中找到规律,因此接下来的问题是我们如何通过对大量样本的数据,借助于决策树算法把内在的蕴含逻辑归纳出来。回想一下,决策树是通过测试条件进行属性划分的方法,因此决策树的生成首先需要回答的两个问题:
(1) 如何选择测试条件进行分裂?
(2) 什么情况下可以选择结束分裂?
一般而言,我们分类的目标就是希望“一是一,二是二”,因此我们希望原始数据集在通过一个测试条件的划分为两个或以上的数据集时,划分后的数据集能够显得更加的“纯”,即划分后的任一子集都尽可能地属于同一个类别。
关于子集的“纯度”,我们可以通过如下例子理解:
在1936年,我们的“渔夫”(R.A.Fisher)提供了一个可能是机器学习领域中最著名的分类数据集——鸢尾花数据集。

分别从山鸢尾花以及多色鸢尾中各取13个样本,分别利用X(花瓣长度)以及Y(萼片宽度)进行划分,可以看到利用花瓣长度这个特征可以完全准确地把两种类型的鸢尾花分辨出来,而利用萼片宽度这个特征进行划分后,还是存在混合的情况。我们可以认为利用特征X划分后的子集,“纯度”更高.
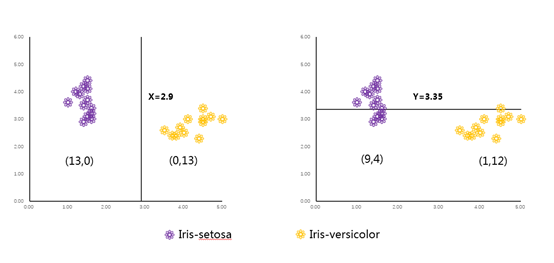
显然,在树模型生成的过程中,对于每一次的划分,我们应该选择可以到令子集纯度更高的划分条件进行。而随着数据集的不断划分,我们的子集纯度越来越高,直至该节点下的样本都属于同一类别。那么什么时候应该终止分裂?一个直觉性的答案显然可以是“该节点下的所有样本都属于同一类别(不需要再进行划分)”或“该节点下的所有样本属性都一样(继续划分下去也不能改善结果)”。下图展示了决策树的生长过程:
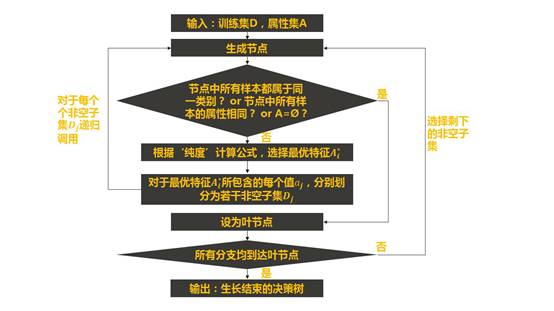
从上面的决策树生长流程图我们可以发现,决策树的生长重点在于其中的“纯度”计算公式,也就是怎么选择最优特征过程,接下啦,我们将简单介绍各个不同决策树算法的划分方法。
(1)ID3系列算法:使用信息熵作为集合纯度的评估
假设我们的样本集合D中含m类样本,其中每一类样本的比例分别为
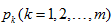
则集合D的信息熵我们定义为:
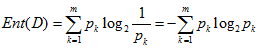
计算时,定义有0log0=0.
ENT(D)越大,集合D的不纯程度越高越小;ENT(D)越小 集合D的纯度越高。因此也有一些文献中提到信息熵用以衡量样本集合的“不纯”纯度。
关于信息熵的通俗介绍,可查看文章:如何通俗地理解决策树中的信息熵
(2)CART算法:使用GINI系数作为集合纯度的评估:
对于集合 D,其纯度的对应计算公式为:
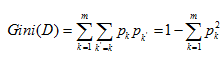
其中m为目标变量的类别个数。与信息熵类似,基尼指数越低,代表集集合的纯度越高。当该节点只含有一个类别时,基尼指数取得最小值0.
由于每个算法的内容比较多,本期只简单介绍一下决策树概念性问题,在下一期,将为大家详细介绍决策树中最为经典的ID3系列算法。

 随时随地看视频
随时随地看视频




