【动态规划】多重背包问题-原创手记-慕课网

说明

前面已经介绍完了01背包和完全背包，今天介绍最后一种背包问题——多重背包。

这个背包，听起来就很麻烦的样子。别慌，只要你理解了前面的两种背包问题，拿下多重背包简直小菜一碟。

如果没有看过前两篇01背包和完全背包的文章，强烈建议先阅读一下，因为本文跟前两篇文章关联性很强。

多重背包

有N种物品和一个容量为T的背包，第i种物品最多有M[i]件可用，价值为P[i]，体积为V[i]，求解：选哪些物品放入背包，可以使得这些物品的价值最大，并且体积总和不超过背包容量。

对比一下完全背包，其实只是多了一个限制条件，完全背包问题中，物品可以选择任意多件，只要你装得下，装多少件都行。

但多重背包就不一样了，每种物品都有指定的数量限制，所以不是你想装，就能一直装的。

举个栗子：有A、B、C三种物品，相应的数量、价格和占用空间如下图：

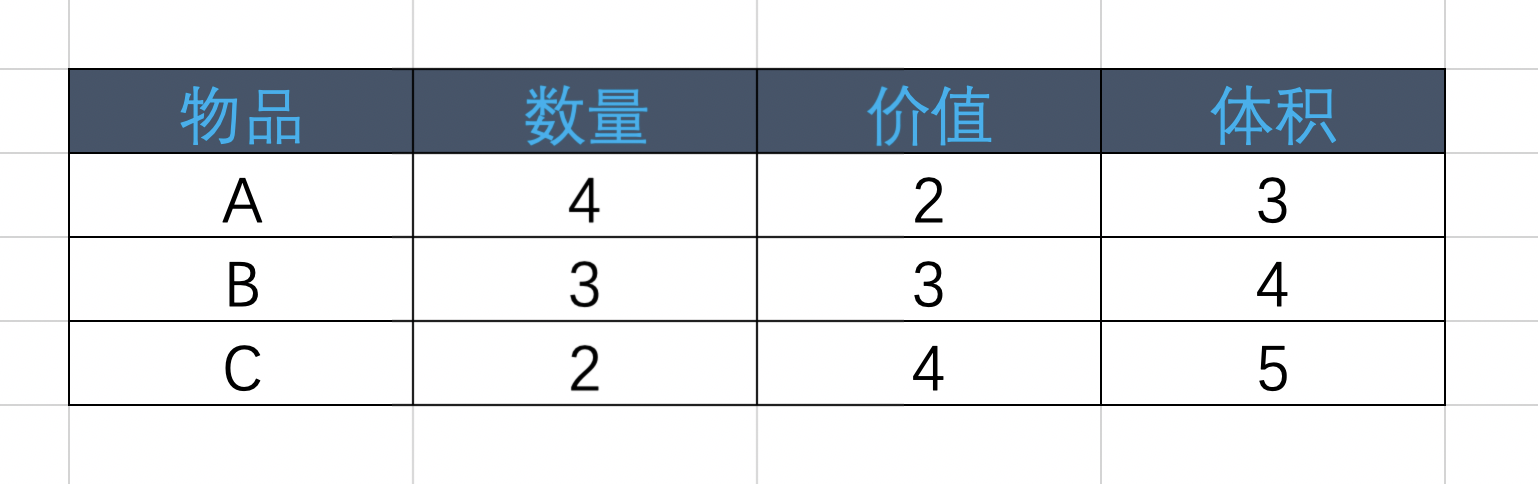
跟完全背包一样，贪心算法在这里也不适用，我就不重复说明了，大家可以回到上一篇中看看说明。

递归法

还是用之前的套路，我们先来用递归把这个问题解决一次。

用ks(i,t)表示前i种物品放入一个容量为t的背包获得的最大价值，那么对于第i种物品，我们有k种选择，0 <= k <= M[i] && 0 <= k * V[i] <= t，即可以选择0、1、2…M[i]个第i种物品，所以递推表达式为：

ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; （0 <= k <= M[i] && 0 <= k * V[i] <= t）

同时，ks(0,t)=0;ks(i,0)=0;

对比一下完全背包的递推关系式：

ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; （0 <= k * V[i] <= t）

简直一毛一样，只是k多了一个限制条件而已。

使用上面的栗子，我们可以先写出递归解法：

public static class MultiKnapsack {
    private static int[] P={0,2,3,4};
    private static int[] V={0,3,4,5};
    private static int[] M={0,4,3,2};
    private static int T = 15;

    @Test
    public void soleve1() {
        int result = ks(P.length - 1,T);
        System.out.println("最大价值为：" + result);
    }

    private int ks(int i, int t){
        int result = 0;
        if (i == 0 || t == 0){
            // 初始条件
            result = 0;
        } else if(V[i] > t){
            // 装不下该珠宝
            result = ks(i-1, t);
        } else {
            // 可以装下
            // 取k个物品i，取其中使得总价值最大的k
            for (int k = 0; k <= M[i] && k * V[i] <= t; k++){
                int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
                if (tmp2 > result){
                    result = tmp2;
                }
            }
        }
        return result;
    }
}

同样，这里的数组P/V/M分别添加了一个元素0，是为了减少越界判断而做的简单处理，运行如下：

最大价值为：11

对比一下完全背包中的递归解法：

private int ks(int i, int t){
    int result = 0;
    if (i == 0 || t == 0){
        // 初始条件
        result = 0;
    } else if(V[i] > t){
        // 装不下该珠宝
        result = ks(i-1, t);
    } else {
        // 可以装下
        // 取k个物品i，取其中使得总价值最大的k
        for (int k = 0; k * V[i] <= t; k++){
            int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
            if (tmp2 > result){
                result = tmp2;
            }
        }
    }
    return result;
}

仅仅多了一个判断条件而已，所以只要弄懂了完全背包，多重背包就不值一提了。

最优化原理和无后效性的证明跟多重背包基本一致，所以就不重复证明了。

动态规划

参考完全背包的动态规划解法，就很容易写出多重背包的动态规划解法。

自上而下记忆法

ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; （0 <= k <= M[i] && 0 <= k * V[i] <= t）

public static class MultiKnapsack {
    private static int[] P={0,2,3,4};
    private static int[] V={0,3,4,5};
    private static int[] M={0,4,3,2};
    private static int T = 15;

    private Integer[][] results = new Integer[P.length + 1][T + 1];

    @Test
    public void solve2() {
        int result = ks2(P.length - 1,T);
        System.out.println("最大价值为：" + result);
    }

    private int ks2(int i, int t){
        // 如果该结果已经被计算，那么直接返回
        if (results[i][t] != null) return results[i][t];
        int result = 0;
        if (i == 0 || t == 0){
            // 初始条件
            result = 0;
        } else if(V[i] > t){
            // 装不下该珠宝
            result = ks2(i-1, t);
        } else {
            // 可以装下
            // 取k个物品，取其中使得价值最大的
            for (int k = 0; k <= M[i] && k * V[i] <= t; k++){
                int tmp2 = ks2(i-1, t - V[i] * k) + P[i] * k;
                if (tmp2 > result){
                    result = tmp2;
                }
            }
        }
        results[i][t] = result;
        return result;
    }
}

这里其实只是照葫芦画瓢。

自下而上填表法

同样也可以使用填表法来解决，此时需要将数组P、V、M额外添加的元素0去掉。

除了k的限制不一样之外，其他地方跟完全背包的解法完全一致：

public static class MultiKnapsack {
    private static int[] P={2,3,4};
    private static int[] V={3,4,5};
    private static int[] M={4,3,2};
    private static int T = 15;

    private int[][] dp = new int[P.length + 1][T + 1];

    @Test
    public void solve3() {
        for (int i = 0; i < P.length; i++){
            for (int j = 0; j <= T; j++){
                for (int k = 0; k <= M[i] && k * V[i] <= j; k++){
                    dp[i+1][j] = Math.max(dp[i+1][j], dp[i][j-k * V[i]] + k * P[i]);
                }
            }
        }
        System.out.println("最大价值为：" + dp[P.length][T]);
    }
}

跟01背包问题一样，完全背包的空间复杂度也可以进行优化，具体思路这里就不重复介绍了，可以翻看前面的01背包问题优化篇。

优化后的状态转移方程为：

ks(t) = max{ks(t), ks(t - Vi) + Pi}

public static class MultiKnapsack {
    private static int[] P={2,3,4};
    private static int[] V={3,4,5};
    private static int[] M={4,3,2};
    private static int T = 15;

    private int[] newResults = new int[T + 1];

    @Test
    public void resolve4() {
        int result = ksp(P.length,T);
        System.out.println(result);
    }

    private int ksp(int i, int t){
        // 开始填表
        for (int m = 0; m < i; m++){
            // 考虑第m个物品
            // 分两种情况
            // 1： M[m] * V[m] > T 则可以当做完全背包问题来处理
            if (M[m] * V[m] >= T) {
                for (int n = V[m]; n <= t ; n++) {
                    newResults[n] = Math.max(newResults[n], newResults[n - V[m]] + P[m]);
                }
            } else {
                // 2： M[m] * V[m] < T 则需要在 newResults[n-V[m]*k] + P[m] * k 中找到最大值，0 <= k <= M[m]
                for (int n = V[m]; n <= t ; n++) {
                    int k = 1;
                    while (k < M[m] && n > V[m] * k ){
                        newResults[n] = Math.max(newResults[n], newResults[n - V[m] * k] + P[m] * k);
                        k++;
                    }
                }
            }
            // 可以在这里输出中间结果
            System.out.println(JSON.toJSONString(newResults));
        }
        return newResults[newResults.length - 1];
    }
}

输出如下：

[0,0,0,0,2,2,2,4,4,4,6,6,6,8,8,8]
[0,0,0,0,2,3,3,4,5,6,6,7,8,9,9,10]
[0,0,0,0,2,3,4,4,5,6,7,8,8,9,10,11]
11

这里有一个较大的不同点，在第二层循环中，需要分两种情况考虑，如果 M[m] * V[m] >= T ，那么第m个物品就可以当做完全背包问题来考虑，而如果 M[m] * V[m] < T，则每次选择时，需要从 newResults[n-V[m]*k] + P[m] * k（0 <= k <= M[m]）中找到最大值。

代码很简单，但要理解却并不容易，为了加深理解，再画一张图：

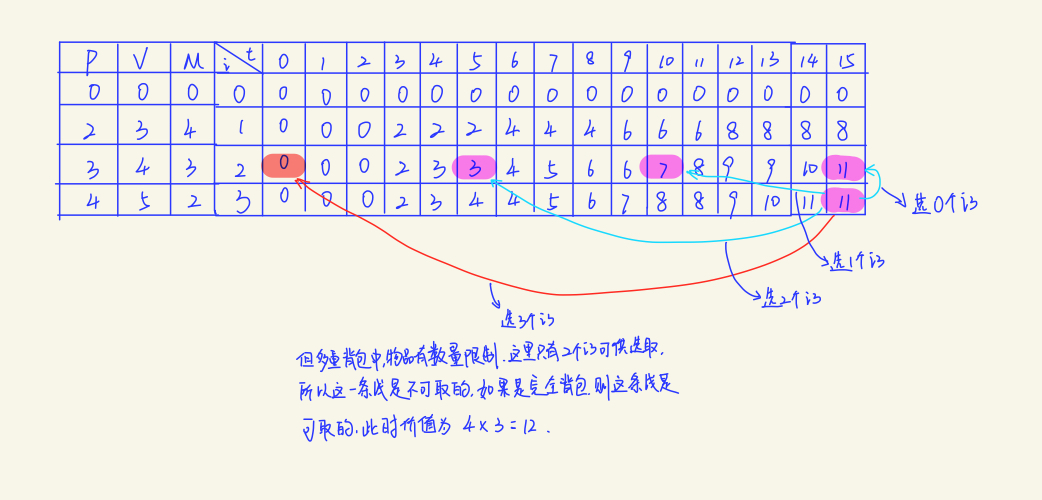
多重背包问题同样也可以转化成01背包问题来求解，因为第i件物品最多选 M[i] 件，于是可以把第i种物品转化为M[i]件体积和价值相同的物品，然后再来求解这个01背包问题。

总结

多重背包问题跟完全背包简直如出一辙，仅仅是比完全背包多一个限制条件而已，如果你回过头去看看前一篇文章，就会发现这篇文章简直就是抄袭。。

关于多重背包问题的解析到此就结束了，三个经典的背包问题到这里就告一段落了。

如果有疑问或者有什么想法，也欢迎关注我进行留言交流：