数据规模
对105的数据进行选择排序,结果计算机假死?
#include <iostream>
#include <cmath>
#include <ctime>
using namespace std;
int main(){
for(int x=1;x<=9;x++){
int n=pow(10,x);
clock_t startTime=clock();
int sum=0;
for(int i=0;i<n;i++)
sum+=i;
clock_t endTime=clock();
cout<<"10^"<<x<<":"<<double(endTime-startTime)/CLOCKS_PER_SEC<<" s"<endl;
}
return 0;
}
如果要想在1s之内解决问题:

空间复杂度
- 多开一个辅助的数组:O(n)
- 多开一个辅助的二维数组:O(n2)
- 多开常数空间:O(1)
- 递归调用是有空间代价的
- 递归的深度是多少,整个递归所占的空间复杂度就是多少
- 递归调用是把递归调用前的函数状态压入系统栈中的
空间复杂度O(1)
int sum1(int n){
assert(n>=0);
int ret=0;
for( int i=0;i<=n;i++)
ret+=i;
return ret;
}
空间复杂度O(n)
int sum2(int n){
assert(n>=0);
if(n==0)
return 0;
return n+sum2(n-1);
}
时间复杂度
时间复杂度:算法中某个特定步骤的执行次数/对于总执行时间的估算成本,随着「数据规模」的增大时,增长的形式。
- n表示数据规模
- Of(n))表示运行算法所需要执行的指令数,和f(n)成正比。
- 因为常数的存在。
- 在学术界,严格地讲,O(f(n))表示算法执行的上界
- 归并排序算法的时间复杂度是O(nlogn)的,同时也是O(n2)
- 在业界,我们就使用O来表示算法执行的最低上界
- 我们一般不会说归并排序是O(n2)的
- 并不是所有的双层循环都是O(n^2)的
O(1)
void swapTwoInts(int &a,int &b){
int temp=a;
a=b;
b=temp;
}
O(n)
int sum( int n){
int ret=0;
for( int i=0:i<=n;i++)
ret+=i;
return ret;
}
void reverse( string &s){
int n=s.size();
for(int i=0;i<n/2;i++)
swap(s[i],s[n-1-i]);
}
//1/2*n次swap操作:O(n)




复杂度实验来确定复杂度
我们自以为写出了一个O(nlogn)的算法,但实际是O(n2)的算法?
- 数据规模的概念
- 如果要想在1s之内解决问题:
- O(n2)的算法可以处理大约104级别的数据;
- O(n)的算法可以处理大约108级别的数据;
- O(nlogn)的算法可以处理大约107级别的数据
- 如果要想在1s之内解决问题:
- 复杂度试验
- 实验,观察趋势
- 每次将数据规模提高两倍,看时间的变化
// O(N) 两倍增加
int findMax( int arr[], int n ){
assert( n > 0 );
int res = arr[0];
for( int i = 1 ; i < n ; i ++ )
if( arr[i] > res )
res = arr[i];
return res;
}
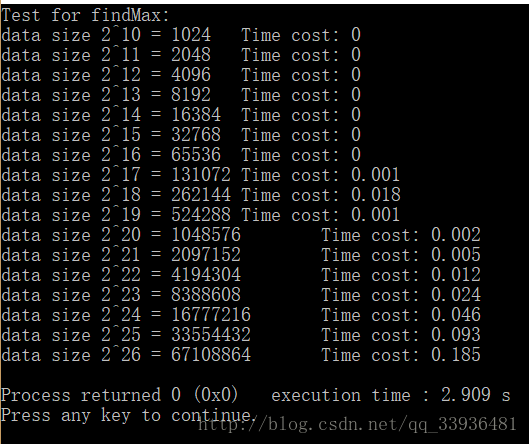
- 随后,O(n^2),数据规模乘二,时间复杂度乘4……
- 随着数据的增加,可以看到O(logN)
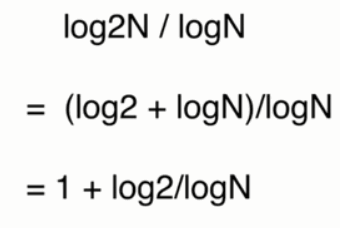
递归算法时间复杂度分析
- 不是有递归的函数就一定是O(nlogn)
- 深入:主定理

均摊复杂度(Amortized Time)
均摊分析和平均情况时间复杂度,前者是一个序列的操作取平均值,后者是针对不同输入来计算平均值
**动态数组(Vector)**每一个操作增加一个元素,删除一个元素相应的复杂度,就需要Amortized Time
动态栈,动态队列类似(数组)
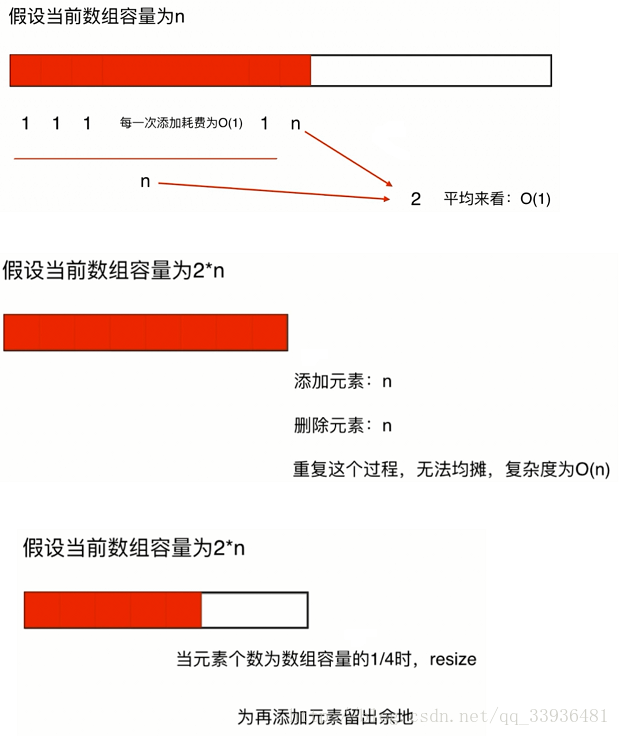
复杂度震荡
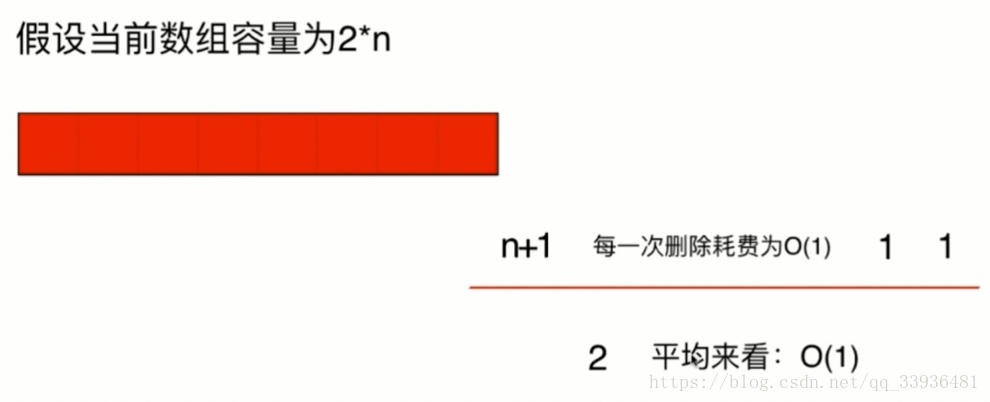
当我们进行resize操作时,也就是在有值的数组还剩一半的时候,我们需要减去剩下的一半空数组;但是当我们再要添加一个元素时,我们也要增加一半的数组的容量,这步操作时间复杂度是O(n),如果我们在这个临界点不停的添加元素,删除元素的话,此时也就无法进行均摊,时间复杂度为0(n)
所以,我们为了避免复杂度震荡,可以尝试这种策略:当元素个数为数组容量的四分之一时,resize。这样可以为再添加的元素留出余地,这时,平均来看,我们的时间复杂度还是O(1)的
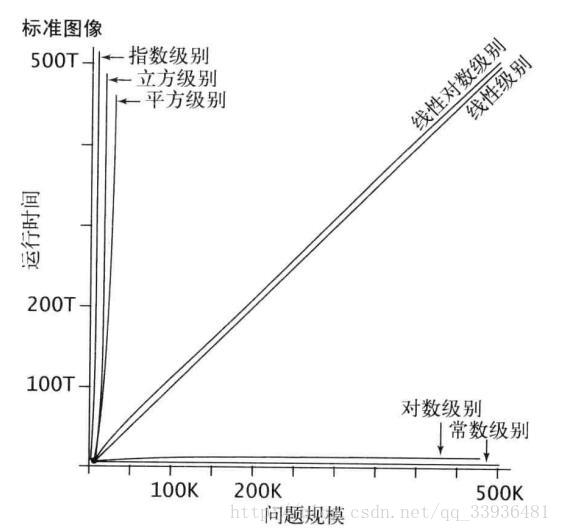
常见算法

a,b,c,d是常数(依据于具体算法),可见,随着数据的增加,是和n的变化幅度有关系的。
O()描述的是一个量级上的差距,当n达到一个数值时,时间复杂度低的算法一定比时间复杂度高的算法快,n越大优化效果越明显,相反的,大部分时间复杂度高的算法前面的常数占有优势,所以我们在处理数据规模小到一定程度,可以使用常数小的时间复杂度高的算法(插入排序法),优化效率大约在10%到15%左右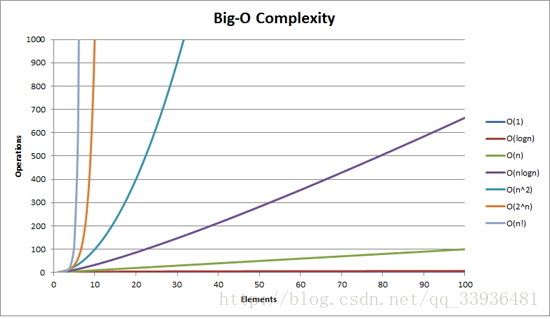

关于大O更详细的解释 https://stackoverflow.com/questions/487258/what-is-a-plain-english-explanation-of-big-o-notation
- 如果一个算法有两部分的话,以以量级最高的时间复杂度为主导。
- O( nlogn+n)=O( nlogn)
- O( nlogn+n2)=O(n2)
- O(AlogA+B)
- O(AlogA+B2)
- 对邻接表实现的图进行遍历:
- 时间复杂度:O(V+E)
- V是图中顶点个数,E是图中边的个数。V和E没有关系。如果是稠密图,完全图,E近乎V^2,同时也是邻接矩阵遍历图的复杂度.
- 算法复杂度在有些情况是用例相关的
问题

- n个字符串,每个字符串进行排序(nlogn)->所以n*nlogn
- 字典序排序nlogn
- 错误的思考
- 将字符串长度和数组长度混淆,数组中每个字符串有多长和数组有多少个字符串,无关系

- 排序算法nlogn表示比较的次数,整形数组通常只需要nlogn次比较,时间复杂度O(1)。字符串比较要依据字典序,所以时间复杂度O(s)
面试准备
要求:
- 算法思路
- 算法素质
- 思考方向(方式)
- 算法优秀不代表技术优秀(算法只是技术的一部分)
- 算法考虑问题全面
- 对问题的理解深入
- 对问题的独到见解:优化,代码规范,容错性
如果是非常难的问题,对你的竞争对手来说,也是难的。关键在于你所表达出的解决问题的思路。甚至通过表达解题思路的方向,得出结论:这个问题的解决方案,应该在哪一个领域,我可以通过查阅或者进一步学习解决问题。
技术面试只是面试的一部分。面试不仅仅是考察你的技术水平,还是了解你的过去以及形成的思考行为方式。
技术:
- 参与项目,项目达到需求,然后完善
- 工作人士,研究生,本科生(毕业设计,其他课程设计)
- 实习找不到
- 在线教育
- 自己做应用,做得恶心?自己用(计划表,备忘录,播放器)
- 自己解决小问题:小爬虫,数据分析,词频统计
- 总结书籍代码
- 博客分享,github
常见问题
- 项目经历和项目中遇到的实际问题
- 你遇到的印象最深的bug是什么?
- 面向对象
- 设计模式
- 网络相关;安全相关;内存相关;并发相关;…
- 系统设计;scalability
- 通过过去了解你的思考行为方式
- 遇到的最大的挑战?
- 犯过的错误?
- 遭遇的失败?
- 最享受的工作内容?
- 遇到冲突的处理方式?
- 做的最与众不同的事儿?
- 问面试官
- 整个小组的大概运行模式是怎样的?
- 整个项目的后续规划是如何的?
- 这个产品中的某个问题是如何解决的?
- 为什么会选择某些技术?标准?
- 我对某个技术很感兴趣,在你的小组中我会有怎样的机会深入这种技术?
- 学习《算法导论》对于智商一般的人来说,切忌完美主义。挫败感。(最好的就是理解一个算法后,再带着目的去深入理解推导)
- 《算法导论》强调理论证明
- 信息学竞赛(ACM)和算法面试有差距
- 高级数据结构和算法面试提及的概率很低
- 红黑树
- 计算几何
- B-Tree
- 数论
- 斐波那契堆
- FFT
面试准备范围:
- 不要轻视基础算法和数据结构,而只关注“有意思”的题目
- 各种排序算法
- 基础数据结构和算法的实现:如堆、二叉树、图…
- 基础数据结构的使用:如链表、栈、队列、哈希表、图、Trie、并查集.…
- 基础算法:深度优先、广度优先、二分查找、递归.…
- 基本算法思想:递归、分治、回溯搜索、贪心、动态规划…
算法面试问题整体思路:
注意题目中的条件
给定一个有序数组…
- 有一些题目中的条件本质是暗示:
- 设计一个O(nlogn)的算法
- 无需考虑额外的空间
- 数据规模大概是10000
- 有序-二分查找法
- logn 分治法,搜索树,数据排序
- 开辟额外空间来换取时间上的优化
- 数据量小 O(N^2)
- 暴力法
LeetCode 3 Longest Substring Without Repeating Characters
在一个字符串中寻找没有重复字母的最长子串
如”abcabcbb”,则结果为”abc”
如”bbbbb”,则结果为"b”
- 对于字符串s的子串s[i.j]
- 使用O(n2)的算法遍历i,j,可以得到所有的子串s[i…j]
- 使用O(length(si…j]))的算法判断s[i…j]中是否含有重复字母
- 复杂度O(n3),对于n=100的数据,可行
优化算法
- 遍历常见的算法思路
- 遍历常见的数据结构
- 空间和时间的交换(哈希表)
- 预处理信息(排序)
- 在瓶颈处寻找答案:O(nlogn)+O(n2);O(n3)
实际编写(健壮性)
- 极端条件的判断
- 数组空?字符串为空?数量为0?指针为NULL?
- 变量名
- 模块化,复用性
面试过程(沟通):
把这个过程看作是和面试官一起探讨一个问题的解决方案。
对于问题的细节和应用环境,可以和面试官沟通。
这种沟通本身很重要,它暗示着你思考问题的方式。
对一组数据进行排序(快速排序吗?)
- 这组数据有什么样的特征?
- 有没有可能包含有大量重复的元素?
- 如果有这种可能的话,三路快排是更好地选择。
- 是否大部分数据距离它正确的位置很近?是否近乎有序?
- 如果是这样的话,插入排序是更好地选择。
- 是否数据的取值范围非常有限?比如对学生成绩排序。
- 如果是这样的话,计数排序是更好地选择。
- 对排序有什么额外的要求?是否需要稳定排序?
- 如果是的话,归并排序是更好地选择。
- 数据的存储状况是怎样的?是否是使用链表存储的?
- 如果是的话,归并排序是更好地选择。
- 数据的存储状况是怎样的?数据的大小是否可以装载在内存里?
- 数据量很大,或者内存很小,不足以装载在内存里,需要使用外排序算法
- 有没有可能包含有大量重复的元素?
算法实践
- 选择合适的online judge
- 不要偏向于程序设计竞赛的OJ
- Codefroces(俄罗斯)
- topcoder(美国)
- codechef(印度)
- 选择面向面试的OJ
- LeetCode(面试问题)
- HackerRank(分类详细)
- codewars
- 不要偏向于程序设计竞赛的OJ
学习和实践做题要平衡
- (intel)初始序列为18625473的一组数采用堆排序,当建堆(小根堆)完毕时,堆所对应的二叉树中序遍历序列为:()
- A.83251647
- B.32851467
- C.38251674
- D.82351476
- (ali)一组记录排序码为(5、11、7、2、3、17),则利用堆排序方法建立的初始堆为()
- A.(11、5、7、2、3、17)
- B.(11、5、7、2、17、3)
- C.(17、11、7、2、3、5)
- D.(17、11、7、5、3、2)
- E.(17、7、11、3、5、2)
- F(17、7、11、3、2、5)
- (baidu)在图采用邻接表存储时,求最小生成树的Prim算法的时间复杂度为()
- O(n)
- O(n+e)
- O(n/2)
- O(n/3)
- (乐视)对一个含有20个元素的有序数组做二分查找,数组起始下标为1,则查找A[2]的比较序列的下标为()
- A.9、5、4、2
- B.10、5、3、2
- C.9、6、2
- D.20、10、5、3、2

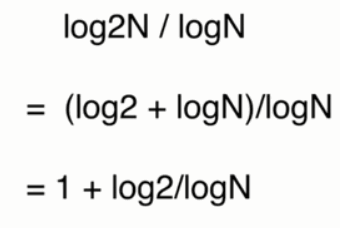




 随时随地看视频
随时随地看视频




