有时,我们想用新技术解决旧技术的包袱,问题是新技术会带来更多的包袱。新技术的一个问题是,人们还不知道它到底有多糟糕。 -《选择乏味的技术》
此手记基于慕课网liuyubobobo老师的线代课程,感谢老师
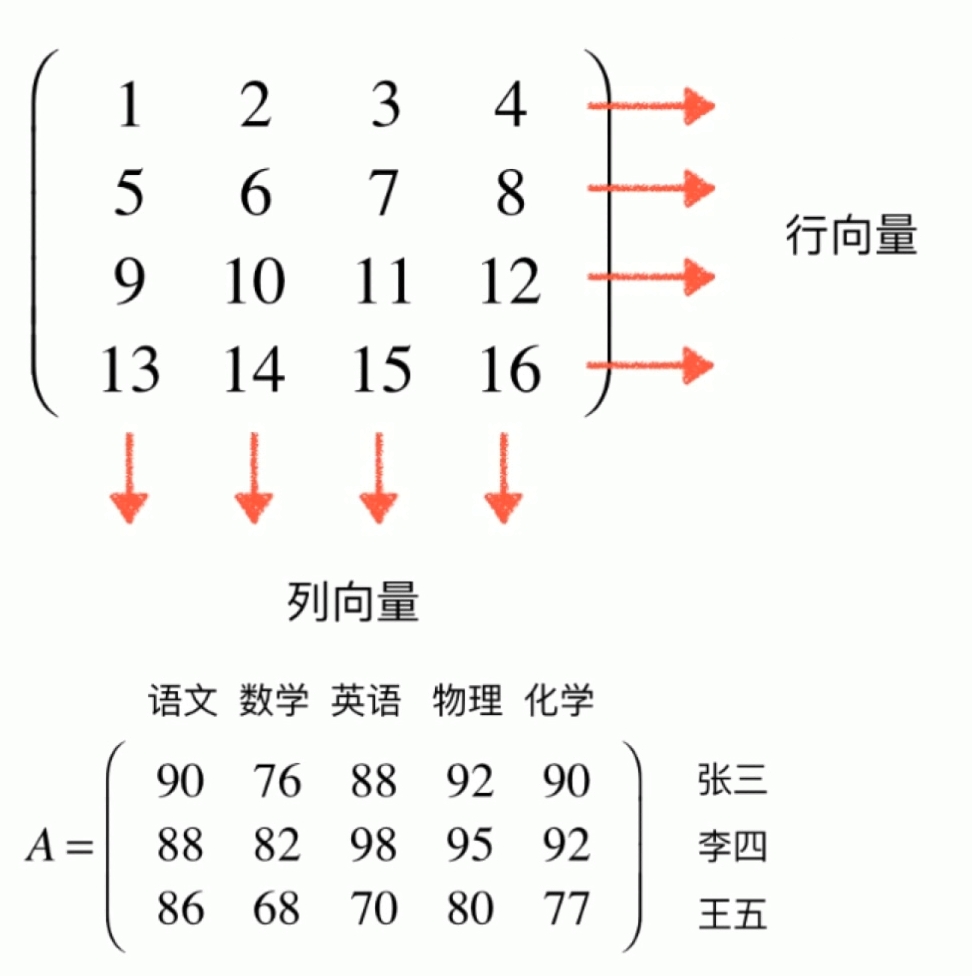
- 大概来说:矩阵是对向量的拓展,一个矩阵表示一组向量
- 行数=列数->方阵
- 方阵有很多特殊的性质
运算

- 基本运算性质
- A+B=B+A
- (A+B)+C=A+(B+C)
- 存在矩阵O,满足:A+O=A
- 存在矩阵-A,满足:A+(-A)=O
- -A唯一,-A=-1·A
- (ck)A=c(kA)
- (c+k)·A=c·A+k·A
- k·(A+B)=k·A+k·B
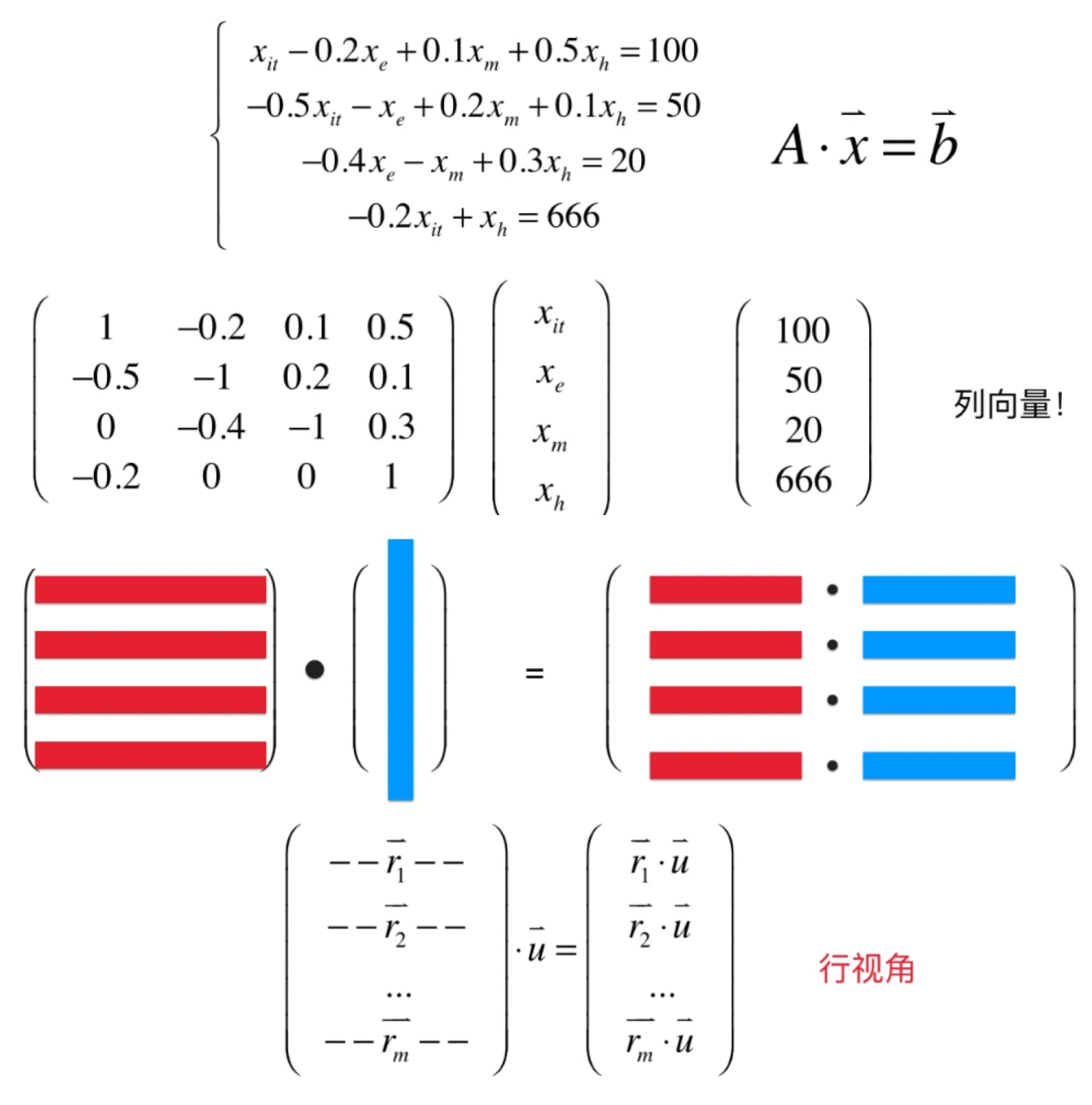
矩阵和向量想乘
- 矩阵A的列数必须和向量u的元素个数一致!
- 矩阵A的行数没有限制
- 矩阵T实际上将向量a转换成了向量b!可以把矩阵理解成向量的函数!
矩阵和矩阵的乘法
- 矩阵A的列数必须和矩阵B的行数一致!
- A是m(行数)*k(列数)的矩阵;B是k(行数)*n(列数)的矩阵,则结果矩阵为m(行数)*n(列数)的矩阵
- 矩阵乘法不遵守交换律!AB≠BA 很有可能根本不能相乘,即使可以相乘,結果也不一樣!
- 矩阵乘法遵守:
- (A·B)·C=A·(B·C)
- A·(B+C)=A·B+A·C
- (B+C)-A=B·A+C·A
- 对任意rc的矩阵A,存在cx的矩阵O,满足:A*O(cx)=O(rx),反之亦然。
- 矩阵的行数列数相等时,可幂。只有方阵才可以进行矩阵的幂运算!
- (A+B)2 ≠ A2+2AB+B2
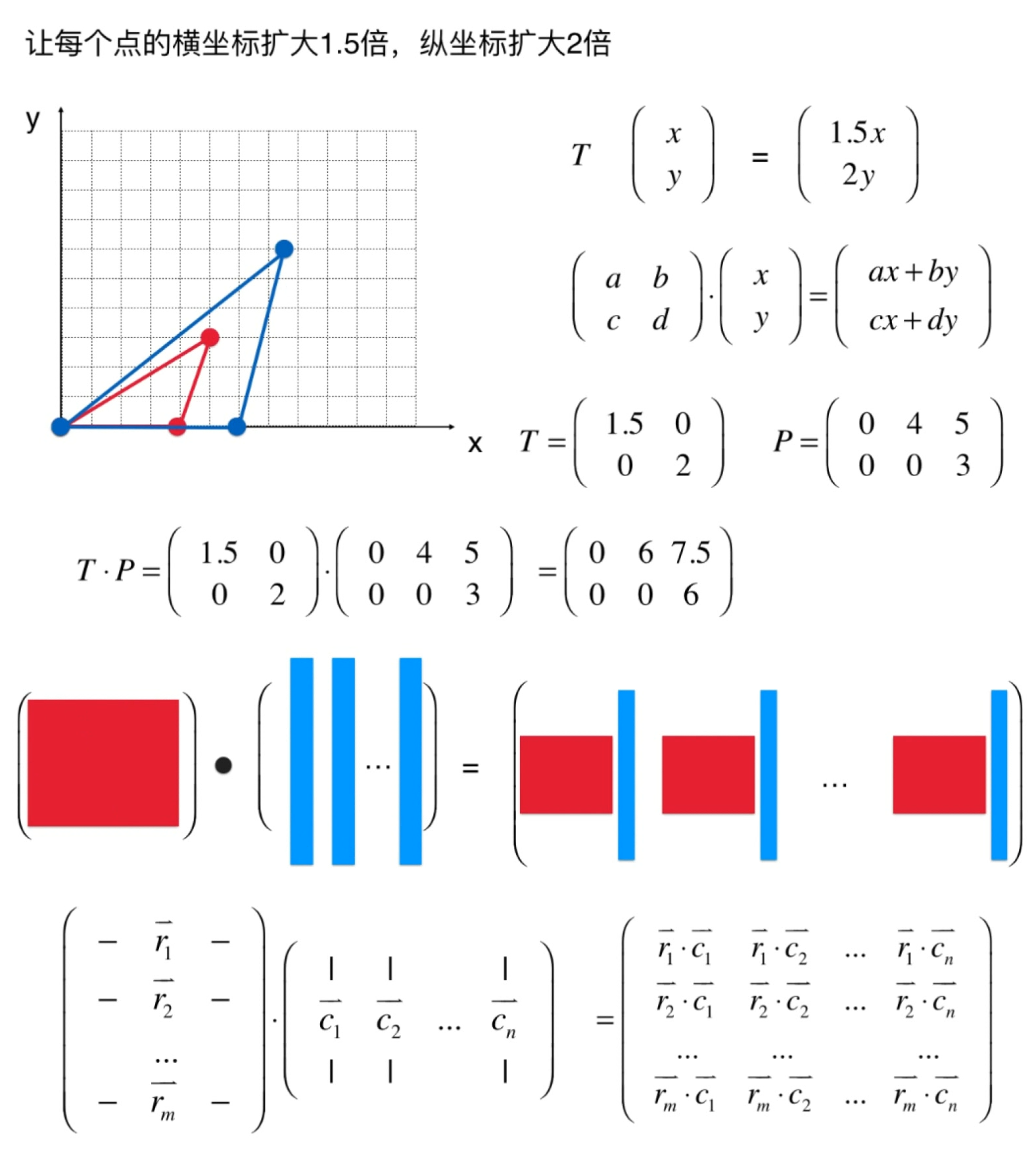
变换矩阵
- 让每个点关于y轴翻转
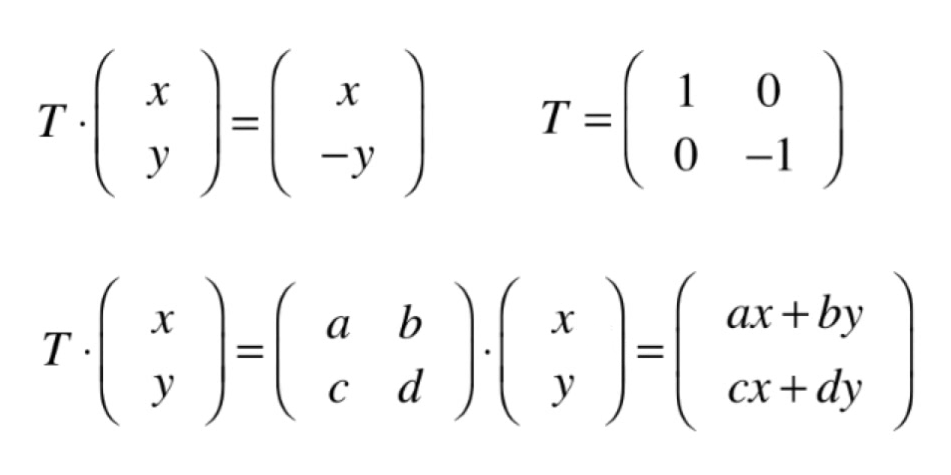
- 让每个点关于x轴翻转

- 让每个点关于原点翻转(x轴,y轴均翻转)
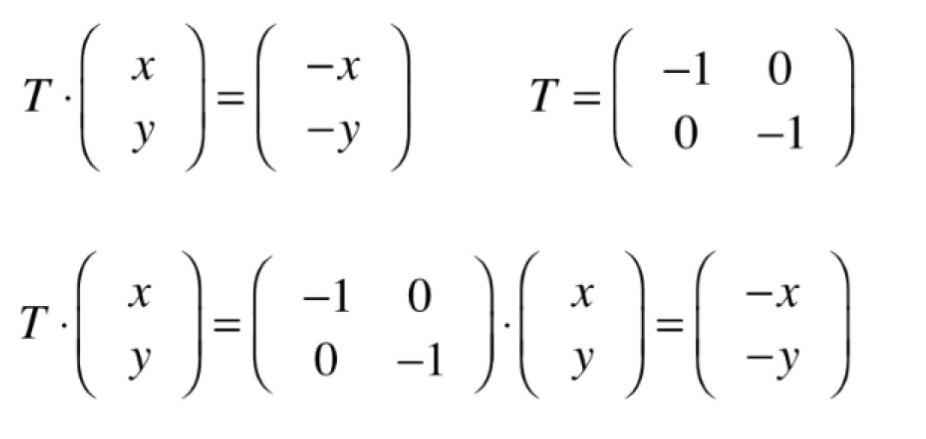
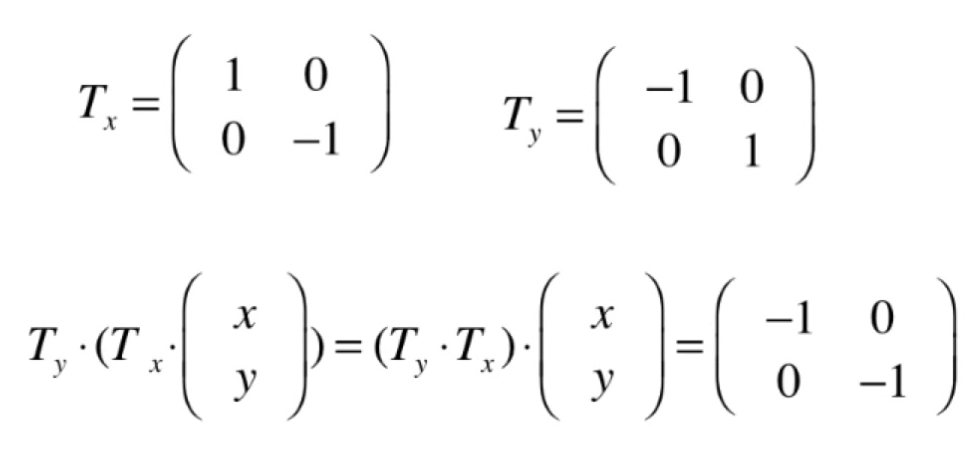
- 沿x方向错切(反之亦然)
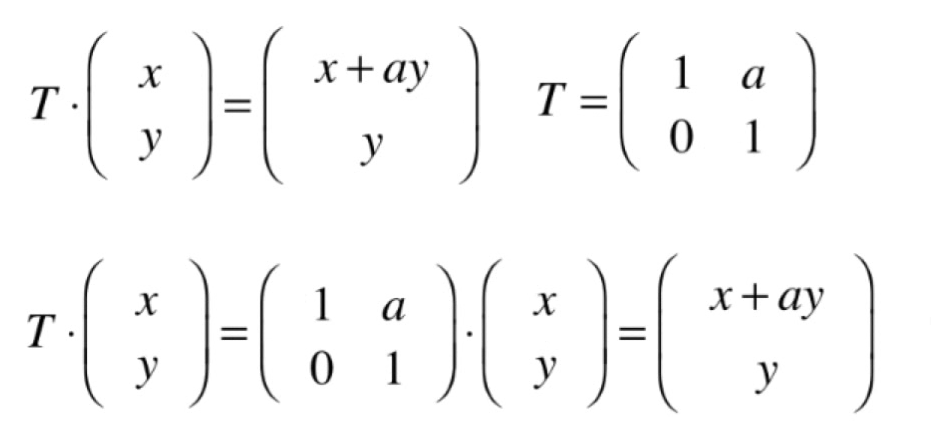
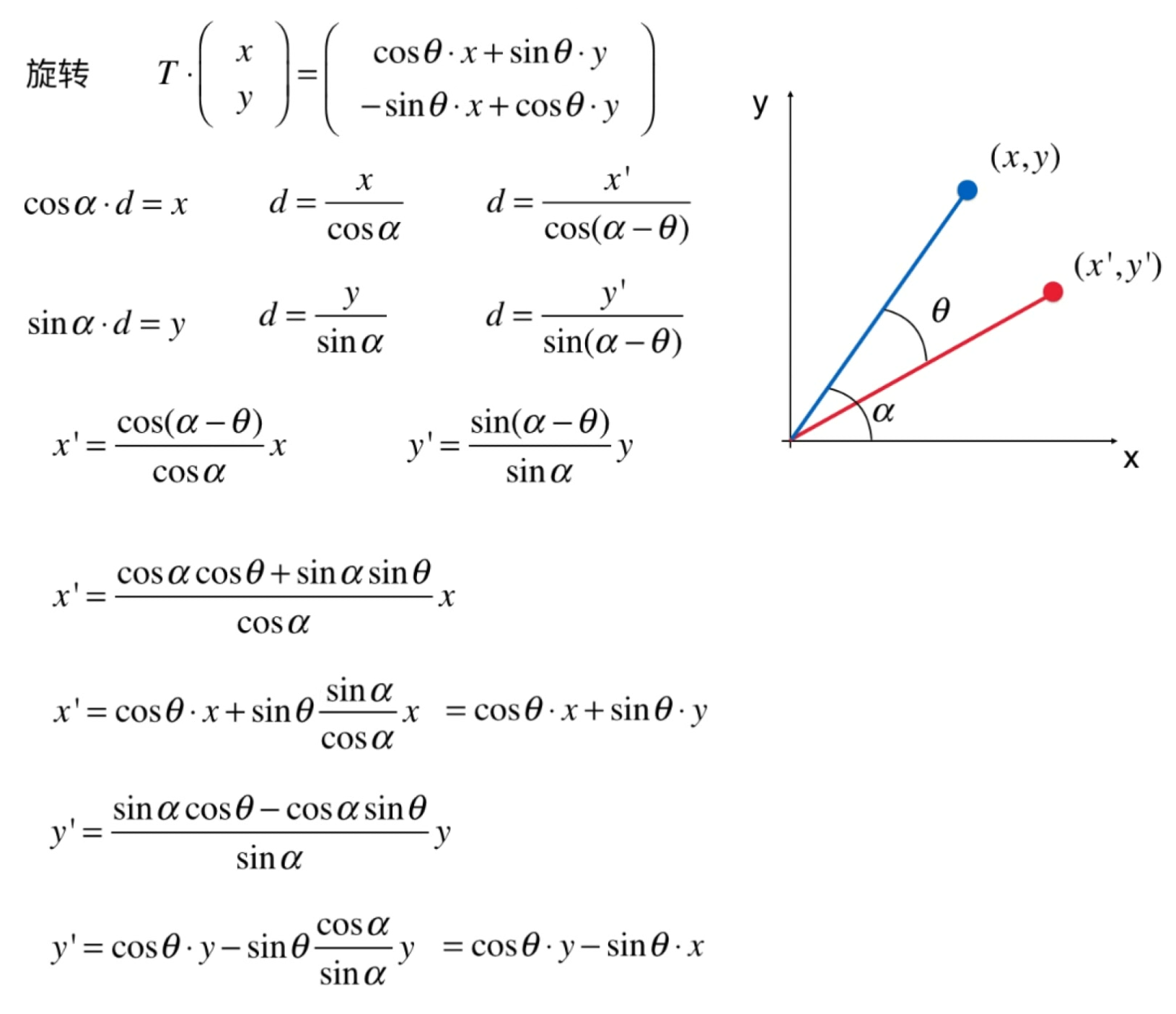
- 旋转角度
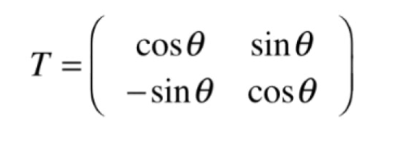
- 平移操作->仿射变换
平移矩阵不是正交矩阵。所有的矩阵运算都是线性变换,所以是仿射、线性变换。可逆,但是逆不等于其转置,所以满秩非正交
单位矩阵
让每个点的横坐标扩大1倍,纵坐标扩大1倍
矩阵的逆
- 矩阵中AB=BA=I,则称B是A的逆矩阵,记做:B=A^(-1)
- A称为可逆矩阵,或者叫非奇异矩阵(non-singular),大多数
- 有些矩阵是不可逆的!称为不可逆矩阵,或者奇异矩阵(singular)
- 如果BA=I,则称B是A的左逆矩阵。
- 如果AC=I,则称C是A的右逆矩阵。
- 如果一个矩阵A既存在左逆矩阵B,又存在右逆矩阵C,则B=C
- 对于矩阵A,存在矩阵B,满足BA=AB=l,矩阵A可逆
- 可逆矩阵一定为方阵!
- 非方阵一定不可逆!
- 转置:行变列,列变行。单位矩阵转置后还是它自己。

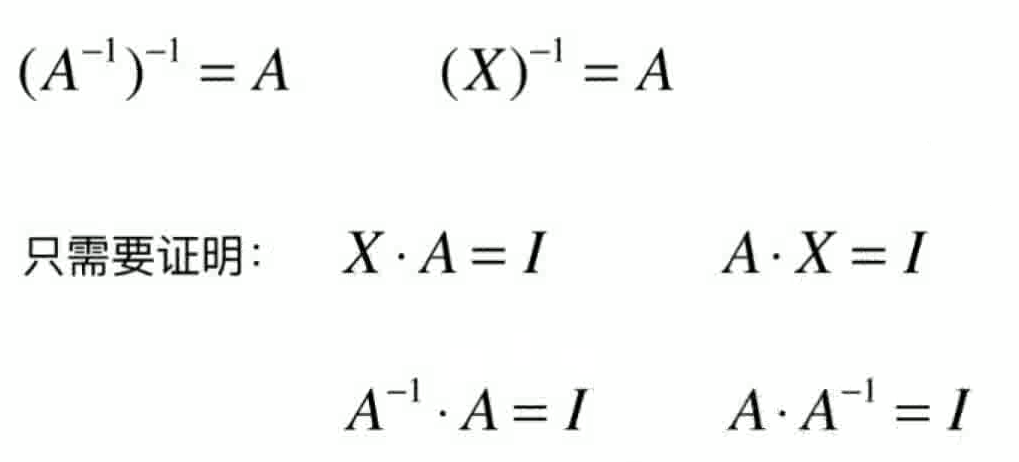
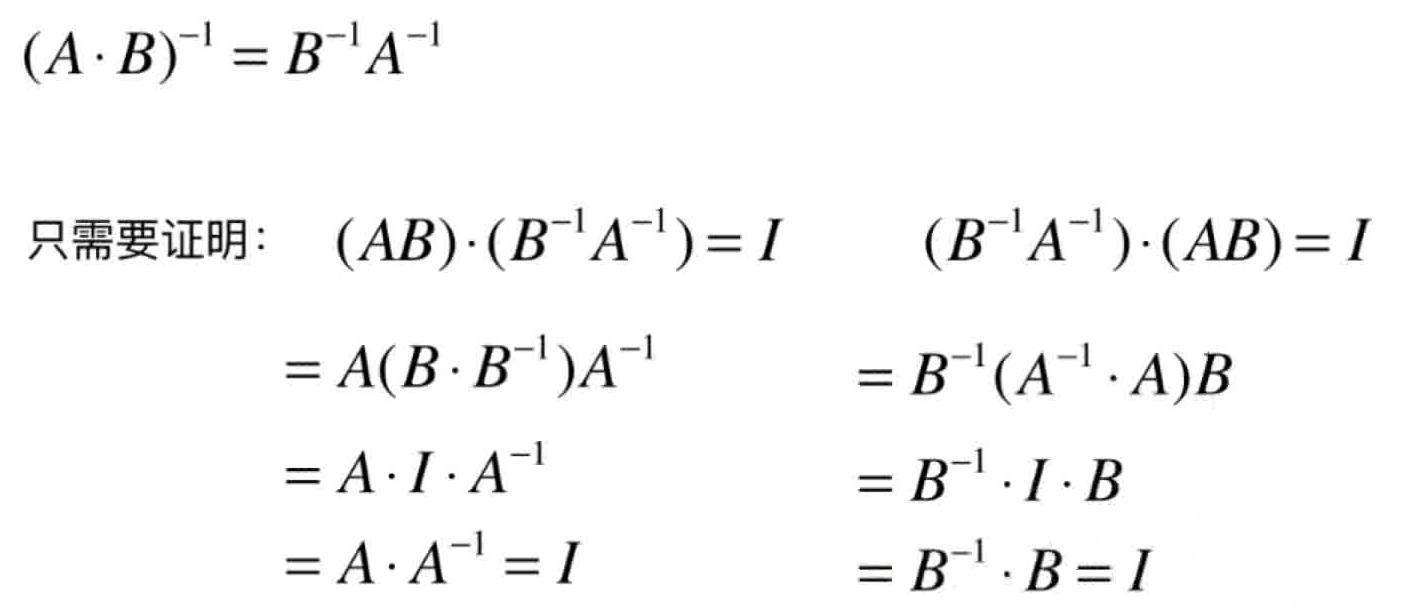


列视角的好处(空间概念的形成)
- 由空间推导变换矩阵
- n维空间应该用n个轴来定义,方阵







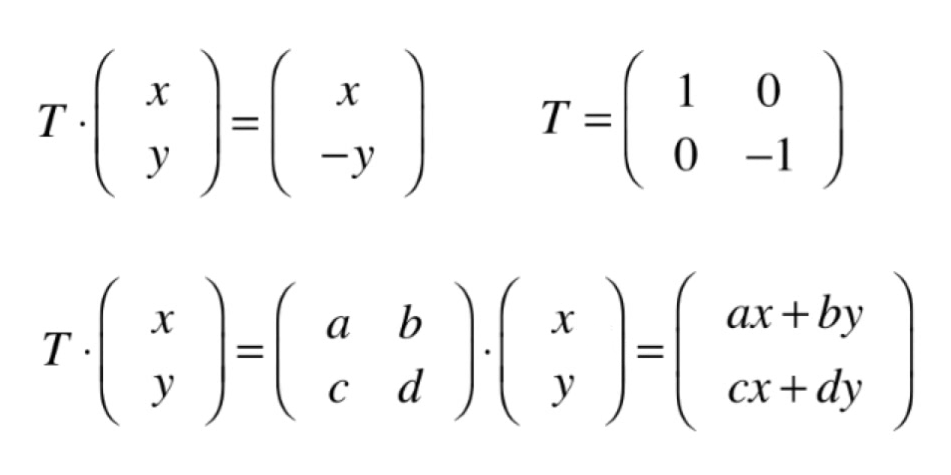
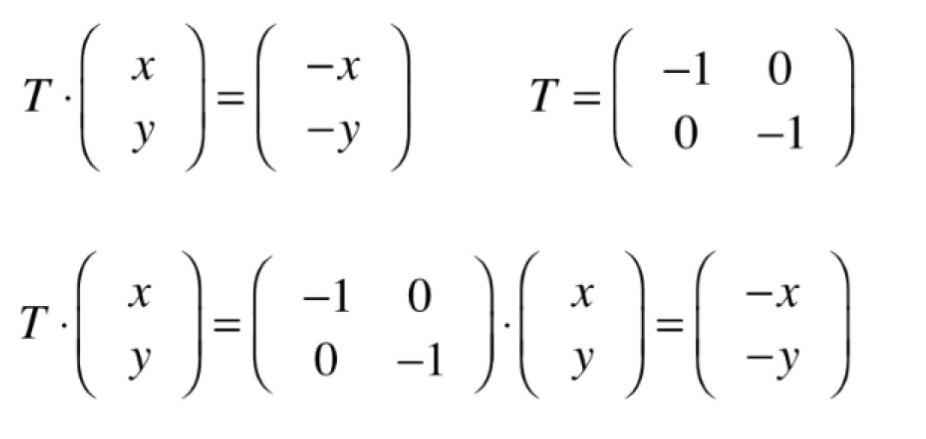
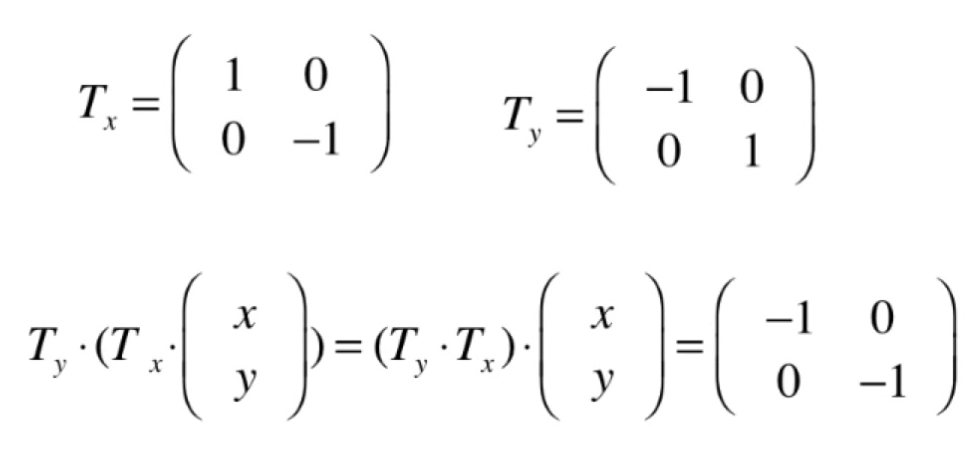
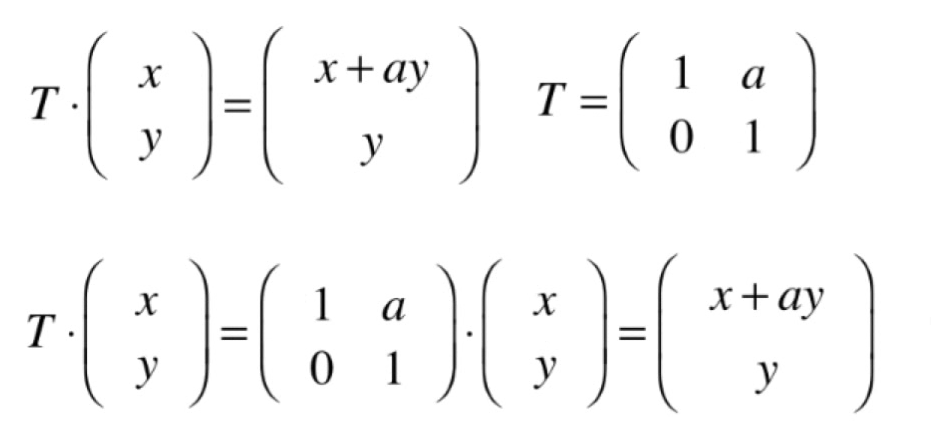

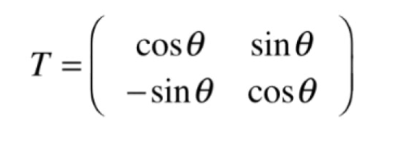





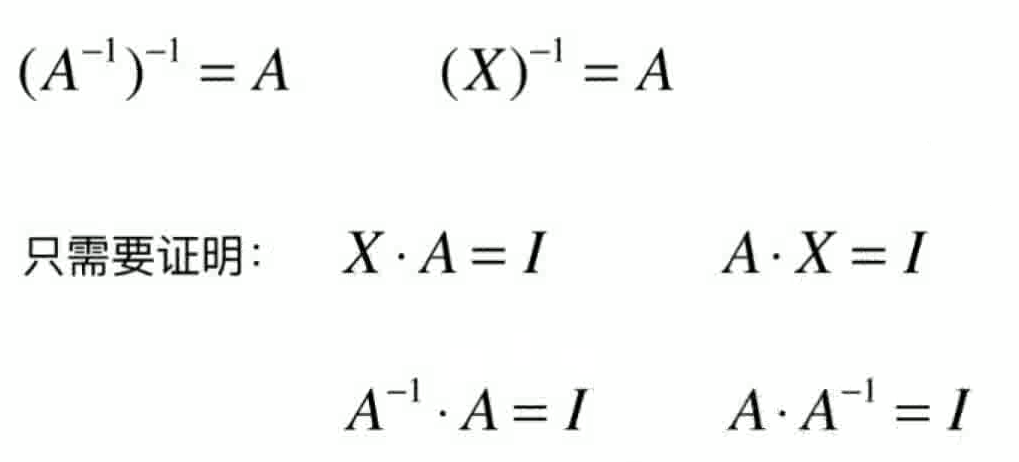
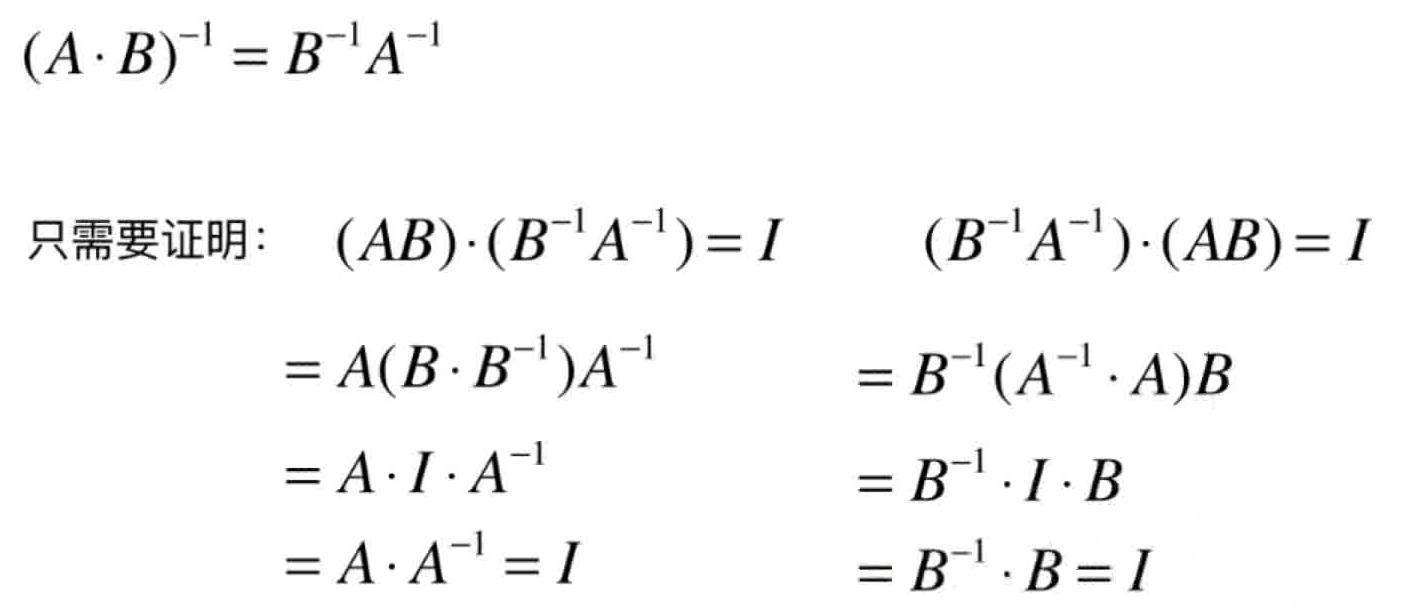



 随时随地看视频
随时随地看视频




