【机器学习】泛化误差评估——过拟合和欠拟合的理解与相关推导-原创手记-慕课网

【模型评估相关概念】

通过机器学习训练出来的数学模型，如果具备很好的泛化能力（即，在训练集和测试集或者更大的数据集中都能很好的决策），那么该模型就是我们理想的训练模型。但是由于训练集质量的影响，往往得不到理想的训练模型，不好的情况一般表现为：过拟合和欠拟合
图片描述

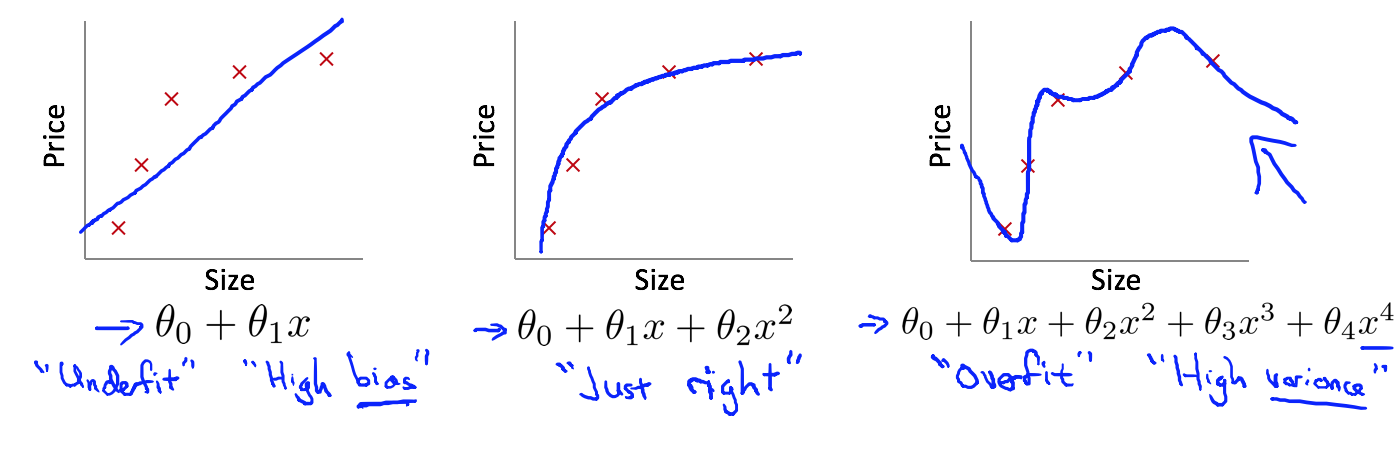
图一表现为欠拟合、图二表示理想的预测模型、图三表现为欠拟合

欠拟合 (高偏差)
欠拟合: 是指模型没有能够很好的学习到数据特征，不能很好的拟合数据，表现为预测值与真实值之前存在较大的偏差。如上图第一个示例。
导致欠拟合的原因: 预测函数的学习能力不足，预测模型过于简单（具体到预测算法模型中就是：特征项不够（包括原始数据的一阶特征和高阶特征））
解决办法:
1. 增加特征项:可以添加额外的属性，也可以组合当前属性，生成高阶属性。进而使学习模型的泛化能力更强。
2. 减少正则化参数:正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。
过拟合(高方差)
过拟合: 模型学习数据的能力太强（复杂的预测函数），除了学习到数据整体的特性以外，还额外学习到了训练集的一些特性，主要表现为能够很好的拟合训练集，但是不能很好的预测测试样本（即，泛化能力太差）
导致过拟合的原因: 预测模型过于复杂（包含过多的特征项：一阶或者高阶），并且往往训练集样本过少。从数学的角度解释：我们在学习线性代数时，给出n个线性无关的方程，我们可以解出来n个变量，但是肯定解不出来n+1个变量。在机器学习中，如果数据数量（对应于方程）远小于模型空间（对应求解的变量），我们只能求解得到部分参数（参数权重 $\theta$ ），而对于另外的部分参数我们无法确定，虽然根据样本我们得到了参数值（ $\theta$ ），但是这部分额外得到的参数值反映的是训练集对应属性的一些分布特性（即包含了训练集本身的特性），故不具备很好的泛化特性，更何况数据中还包含一些不合理的数据样本，综合所有因素，最终导致预测模型能够很好的拟合训练集但是不能很好的拟合测试样本。
解决办法:
1. 增加样本数量:根据原因，导致过拟合的因素是由于训练集样本太少，不具备整体性，所以增加样本数量可以提升泛化能力。
2. 减少变量（属性）数量:与增加样本数量相对，减少无关或者弱相关变量项，可以人工去除，也可以选择相关的算法进行自动去除。
3. 清洗数据:导致过拟合的一个原因也有可能是数据不纯导致的，如果出现了过拟合就需要我们重新清洗数据。
4. 正则化:减少无关（或者弱相关）参数项的权重，即减小对应的 $\theta$ 值。进而降低训练集本身特性的影响。

【泛化性能评估：偏差-方差分解】

这部分内容是作为上一部分内容的补充，通过这部分内容，可以进一步加深对上一部分概念的理解。注意到，上文对欠拟合和过拟合，特意注解为高偏差和高方差。关于这部分的理解，我们主要通过偏差-方差分解来解释。
偏差-方差分解： 试图通过对学习算法的期望泛化错误率进行拆解，来解释学习算法泛化性能，是众多解释学习算法泛化性能的一种重要工具。
我们知道，算法在不同训练集上学得的结果很可能不同，即使这些训练集是来自同一分布。以回归任务为例：
回归任务最常用的性能度量——均方误差：
$E(f;D)=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^2$
更一般的形式，对于数据分布 $D$ 和概率密度函数 $p(\cdot)$ ,均方误差可描述为：
$E(f;D)=\int_{x - D}(f(x)-y)^2p(x)dx$
其中 $x$ 表示测试样本, $y$ 为样本 $x$ 对应的真实标记, $f(x)$ 为训练集 $D$ 上学得模型 $f$ 在 $x$ 上的预测输出，在下面我们将用 $f(x;D)$ 表示，即
$f(x;D)=f(x)$
学习算法的期望预测为：
$\bar{f}(x)=E_D\left[f(x;D)\right]$
使用样本数相同的不同训练集产生的方差：
$var(x)=E_D\left[(f(x;D)-\bar f(x))^2\right]$
噪声为：
$\epsilon^2 =E_D\left[(y_D-y)^2\right]$
其中 $y_D$ 为x在数据集中的标记（数据标记与真实值之间存在噪音误差）， $y$ 为 $x$ 的真实标记
期望输出与真实标记的差别称为偏差（bias）,即
$bias^2(x)=\left(\bar f(x)-y\right)^2$
为便于讨论，假定噪声期望为零，即 $E_D\left[(y_D-y)\right]=0$ .通过简单的多项式展开合并，可对算法的期望泛化误差进行分解：
$\begin{aligned} E(f;D) &=E_D\left[(f(x;D)-y_D)^2\right]\\ &=E_D\left[\left(f(x;D)-\bar f(x)+\bar f(x)-y_D \right)^2\right]\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+E_D\left[(\bar f(x)-y_D)^2\right]\\ & +\color{orange}E_D\left[2\left(f(x;D)-\bar f(x)\right)\left(\bar f(x)-y_D\right)\right] &\text{其中$2E_D\left[\left(f(x;D)-\bar f(x)\right)\right]=0$}\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+E_D\left[(\bar f(x)-y_D)^2\right]\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+E_D\left[\left(\bar f(x)-y+y-y_D\right)^2\right]\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+E_D\left[\left(\bar f(x)-y\right)^2\right]+E_D\left[\left(y-y_D\right)^2\right]\\ &+\color{orange}2E_D\left[\left(\bar f(x)-y\right)\left(y-y_D\right)\right]\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+E_D\left[\left(\bar f(x)-y\right)^2\right]+E_D\left[\left(y-y_D\right)^2\right]\\ &=E_D\left[(f(x;D)-\bar f(x))^2\right]+\left(\bar f(x)-y\right)^2+E_D\left[\left(y-y_D\right)^2\right] \end{aligned}$
于是：
$E(f;D) =bias^2(x)+var(x)+\epsilon^2$
即泛化误差可分解为偏差、方差和噪声之和。回顾偏差、方差、噪声的定义：

偏差：度量学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力（学习能力）
方差：度量同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响（数据的充分性）
噪声：表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度。（学习任务本身的难度）

根据偏差-方差分解公式，泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

偏差-方差窘境

一般来说，偏差与方差是有冲突的，这就是偏差-方差窘境，下图展示了偏差-方差窘境的变化示意图（从网上借的图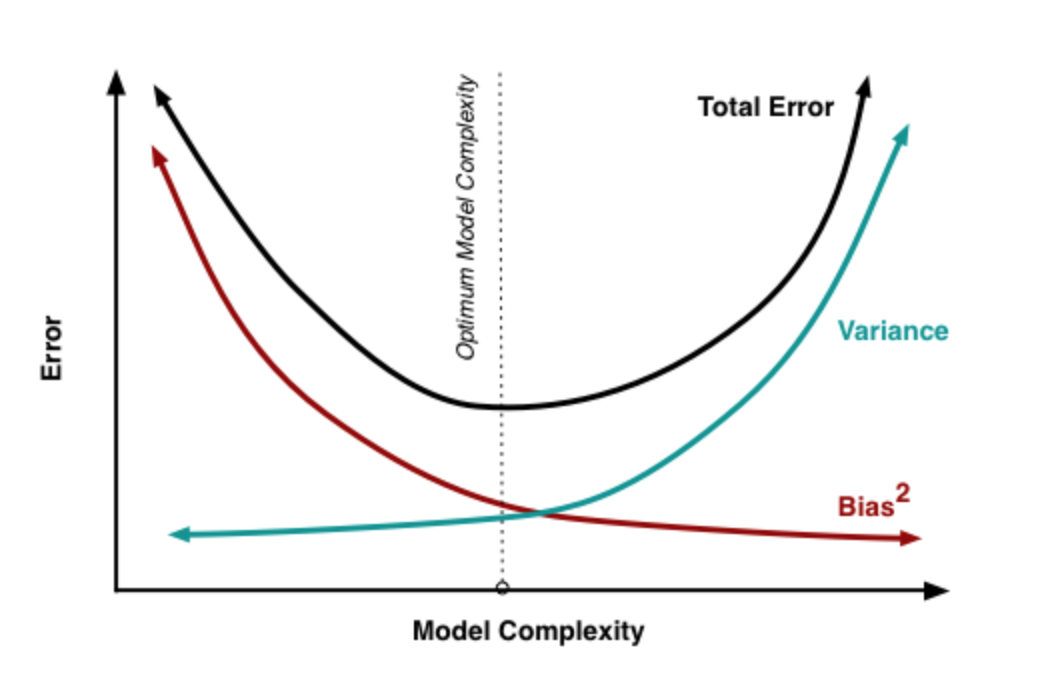）：从别的地方借的图
给定学习任务，假定我们能控制学习算法的训练程度，则在训练不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导了泛化错误率；随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率；在训练程度充足后，学习器的拟合能力已非常强，训练数据发生的轻微扰动都会导致学习器发生显著变化，若训练数据自身的、非全局的特性被学习器学到了，则将发生过拟合。