【机器学习】线性回归——正规方程（多变量）的实现（Python版）-原创手记-慕课网

【相关数学知识】

正规方程，实现线性回归的一种方式。该方式从统计学的角度对线性回归的实现进行了数学推导，你需要具备的知识主要包含如下几个方面：
图片描述
上一篇博客，介绍的是梯度下降法实现的线性回归，主要基于单变量来实现代码，其实完全可以根据变量的个数构造多变量的梯度下降。本篇是线性回归的另一种实现方式，即基于多变量的正规方程。

【数学推导】

通过前面的两篇手记，我们可以这样认为，真实样本数据与预测值之间存在如下的关系：
$y^{(i)}=\theta^{T}\chi+\epsilon^{(i)}$
其中 $\epsilon^{(i)}$ ,表示真实结果与预测结果之间的误差。

前提条件
误差 $\epsilon^{(i)}$ 是独立并且具有相同分布，并且服从均值为0方差为 $\theta^{2}$ 的高斯分布，图示如下：
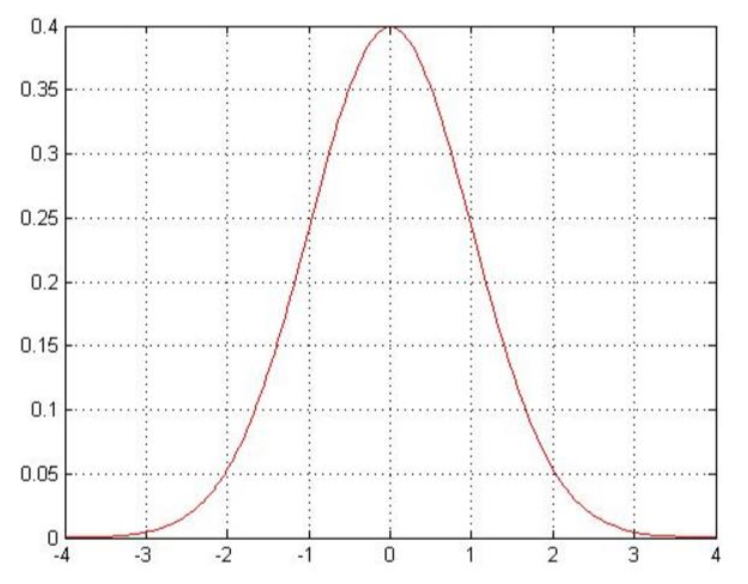
推导过程
预测值与误差： $y^{(i)}=\theta^{T}\chi+\epsilon^{(i)}\qquad{\cdots(1)}$
由于误差服从高斯分布: $\rho(\epsilon^{(i)})=\frac{1}{\sqrt{2\pi}}\exp(-\frac{(\epsilon^{(i)})^{2}}{2\sigma^{2}}) \qquad{\cdots(2)}$
将（1）式带入（2）式可得：
$\rho(y^{(i)}|\chi^{(1)};\theta)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{(y^{(i)}-\theta^{T}\chi^{(i)})^{2}}{2\sigma^{2}})$
似然函数：
$L(\theta)=\prod_{i=1}^{m}\rho(y^{(i)}|\chi^{(1)};\theta)=\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}}\exp(-\frac{(y^{(i)}-\theta^{T}\chi^{(i)})^{2}}{2\sigma^{2}})$
即，在θ取何值的情况下，测试样本出现的概率最大，于是问题便变成了求最大值的问题。
对数似然：
$\log L(\theta)=\log\prod_{i=1}^{m}\frac{1}{\sqrt{2\pi}}\exp(-\frac{(y^{(i)}-\theta^{T}\chi^{(i)})^{2}}{2\sigma^{2}})$
乘法相对难解，加log以后就转换成了加法，结果相对容易，化简得：
$\log L(\theta)=\sum_{i=1}^{m}\log \frac{1}{\sqrt{2\pi}}\exp(-\frac{(y^{(i)}-\theta^{T}\chi^{(i)})^{2}}{2\sigma^{2}})$
进一步化简得到：
$\log L(\theta)=m\log \frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{\sigma^{2}}*\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta^{T}\chi^{(i)})^{2}$
我们的目标，是为了让L(θ)取得最大值，故让似然函数，越大越好，从上式可以看出，第一项是常数项，只有第二项越小越好，故：
$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta^{T}\chi^{(i)})^{2}$
上式一般被称为最小二乘法，同时这个也是我们的代价函数（损失函数）。
对 $J(\theta)$ 进行向量化，注意这里将 $\theta^{T}X^{(i)}$ 转变成了 $X\theta$ (我们实际操作过程中也是这样子)如下所示：
$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(y^{(i)}-\theta^{T}\chi^{(i)})^{2}=\frac{1}{2}(X\theta-y)^{T}(X\theta-y)$
求偏导：
$\nabla_\theta J(\theta)=\nabla_\theta (\frac{1}{2}(X\theta-y)^{T}(X\theta-y))=\nabla_\theta(\frac{1}{2}(\theta^{T}X^{T}-y^{T})(X\theta-y))$
$\nabla_\theta J(\theta)=\nabla_\theta (\frac{1}{2}(\theta^{T}X^{T}X\theta-\theta^{T}X^{T}y-y^{T}X\theta+y^{T}y))$
$\nabla_\theta J(\theta)=\frac{1}{2}(2X^{T}X\theta-X^{T}y-(y^{T}X)^{T})=X^{T}X\theta-X^{T}y$
令 $\nabla_\theta J(\theta)=0$ ,则 $\theta =(X^{T}X)^{-1}X^{T}y$
到此，整个推导过程结束，那么怎样评估，拟合效果好不好？这里我们一般常用如下方法进行评估：
$R^{2}=1-\frac{\sum_{i=1}^{m}(y_{i}^{'}-y_{i})^{2}}{\sum_{i=1}^{m}(y_{i}-\bar{y})^{2}}$
$R^{2}$ 的取值越接近1，表示模型拟合的越好。

代码实现：

#数据集依旧采用吴恩达机器学习教程“ex1data2.txt”
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import numpy.linalg as nlg

def readData(path,name=[]):
    data = pd.read_csv(path,names=name) 
    data = (data - data.mean()) / data.std()
    data.insert(0,'First',1)
    return data

def costFunction(theta,X,Y):
    return (1/2)*(X.dot(theta)-Y.T).T*(X.dot(theta)-Y.T)

def normalFunction(data):
    X=np.matrix(data.iloc[:,0:-1].values)
    Y=np.matrix(data.iloc[:,-1].values)
    theta=nlg.inv(X.T.dot(X)).dot(X.T).dot(Y.T)
    return theta,costFunction(theta,X,Y)


if __name__ == "__main__":
    data = readData('ex1data2.txt',['Size', 'Bedrooms', 'Price'])
    theta,costValue=normalFunction(data)
    print(theta)

与第二篇博客的最终theta进行对比，发现差别不是很大，都是：[[-1.15556179e-16],[ 8.84765988e-01],[-5.31788197e-02]]

【正规方程存在的问题】

正规方程虽然能够一步到位，但是也存在一些问题:公式中若 $(X^{T}X)^{-1}$ 无解（即， $X^{T}X$ 不可逆）我们能否得到理想的 $\theta$ ?
注：我们称不可逆矩阵为奇异矩阵或退化矩阵
一般情况下， $X^{T}X$ 不可逆的情况很少发生，即使发生了，Python函数库中的函数也能够求得 $X^{T}X$ 的逆矩阵。一般发生 $X^{T}X$ 不可逆的情况，主要是因为矩阵没有满秩，即存在相关特征。
故，发生 $X^{T}X$ 不可逆的情况，一般为如下情况：
样本数量m小于或等于特征数量n或特征数量中存在相关特征
对于这种情况，一般我们有两种方式去改善测试数据集：

丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙(例如 PCA)
正则化。保留所有的特征，但是减少参数的大小(magnitude)